Комплексные числа впервые встречаются в работах итальянских математиков, начиная с середины XVI века (Кардано, Бомбелли). К тридцатым годам XIX века была построена не противоречивая теория комплексных чисел (Гаусс, Гамильтон и др.). К этой теории мы и переходим.
Определение 2.1. Упорядоченной парой вещественных чисел называется пара чисел, для которой известно какое число считается первым, а какое вторым.
Определение 2.2. Множеством комплексных чисел называется множество упорядоченных пар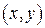 
вещественных чисел 
, для которых определены отношения равенства и операции сложения и умножения по следующим правилам:
a) отношение равенства: две пары равны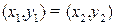 
если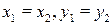 
,
б) сложение: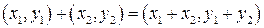 
,
в) умножение: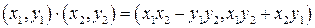 
.
Комплексное число 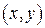, для сокращения записи, будем обозначать буквой z. Действительные числа x и y называют соответственно действительной и мнимой частями комплексного числа z и обозначают символам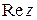и 
и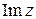 
. Множество всех комплексных чисел обозначают буквой C.
Из определения операций сложения и умножения комплексных чисел вытекают следующие алгебраические законы:
1) 
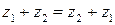‑ коммутативный (или переместительный) закон сложения;
2) 
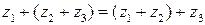‑ ассоциативный (или сочетательный) закон сложения;
3) 
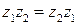‑ коммутативный (или переместительный) закон умножения;
4) 
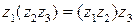‑ ассоциативный (или сочетательный) закон умножения;
5) 
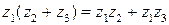‑ дистрибутивный (или распределительный) закон относительно сложения.
Доказательство.
Действительно
1) 
;
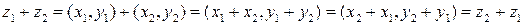2) 
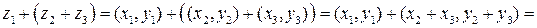
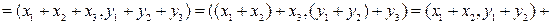
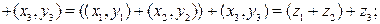
3) 
;
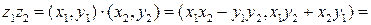
4) 
;
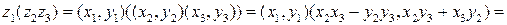
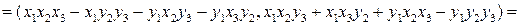
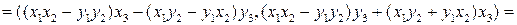
5) 
.
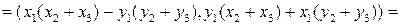
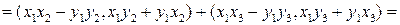
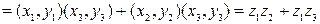Конец доказательства.
Замечание 2.1. Определение операции умножения для комплексных чисел не очевидно, однако именно при таком определении на множестве комплексных чисел отсутствуют делители нуля.
Число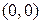 
называется комплексным нулем и обозначается 0. Его роль аналогична роли вещественного нуля:
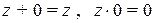
Лемма 2.1. Комплексный ноль единственен.
Доказательство. Пусть существует второе число q, такое что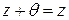 
. Тогда
.
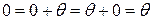Конец доказательства.
Число 
называется противоположным к числу z, если:
.
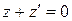Лемма 2.2. Для любого комплексного числа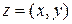 
противоположное к нему число существует и единственено, причем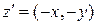 
.
Доказательство. Очевидно, что
.
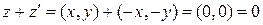Пусть существует второе число 
, такое что 
. Тогда
,
.
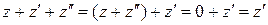Отсюда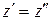 
.
Конец доказательства.
Определение 2.3. Число 
называется единицей и обозначается 1. Ее роль аналогична роли вещественной единице:
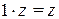для любого 
.
Лемма 2.3. Единица единственена.
Доказательство. Пусть существует второе число 
, такое что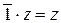 
. Тогда
.
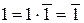Конец доказательства.
Число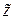 
называется обратным к числу z, если:
.
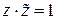Лемма 2.4. Для любого комплексного числа 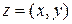, не равного нулю, обратное к нему число 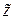существует и единственено, причем 
.
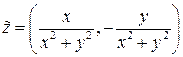Доказательство. Пусть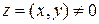 
и 
. Тогда
.
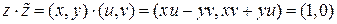Отсюда
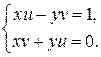
Умножая первое уравнение на x, а второе – на y и складывая, получим
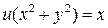или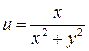 
.
Умножая первое уравнение на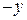 
, а второе – на x и складывая, получим
или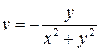 
.
Отсюда найдем обратное к z число
.
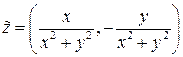Пусть существует второе число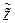 
, такое что 
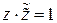. Тогда
,
.
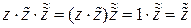Отсюда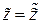 
.
Конец доказательства.
Выделим еще раз свойства операций сложения и умножения комплексных чисел:
1) 
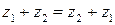(сложение коммутативно);
2) 
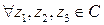
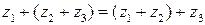(сложение ассоциативно);
3) 
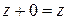(особая роль нуля);
4) 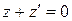(для каждого z существует противоположное число );
5) 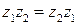(коммутативно);
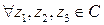
6) 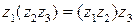(умножение ассоциативно);
7) , 
, 
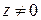, (особая роль единицы);
8) 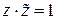, 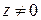(для каждого 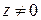существует обратное число );
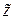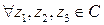
9) 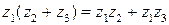(умножение дистрибутивно относительно сложения)
Отсюда заключаем, что относительно операции сложения множество комплексных чисел образует абелеву группу.
Определим теперь операцию вычитания двух комплексных чисел
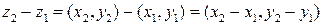
Очевидно, что если 
, то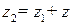 
. Далее, так как верно равенство 
, то по соглашению 
.
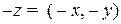Введем теперь операцию деления. Так же как и для вещественных чисел, будем считать комплексное число z результатом деления комплексного числа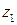 
на комплексное число 
, если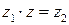 
.
Покажем, что операция деления определена для любых комплексных чисел и 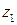, за исключение деления на комплексный ноль. Итак, пусть результат деления 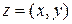, где x и y неизвестны. Имеем
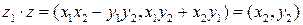
Отсюда получаем алгебраическую систему двух линейных уравнений
Умножим первое уравнение на 
, а второе на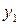 
и сложим, затем умножим первое уравнение на 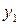, а второе на и вычтем его из первого, тогда получим
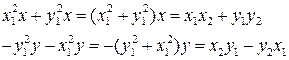
Отсюда
, 
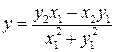
Если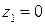 
, то 
и деление невозможно.
Законы алгебраических операций над комплексными числами совпадают с законами алгебраических операций над вещественными числами. Поэтому, все алгебраические соотношения для вещественных чисел переносятся на комплексные числа.
Пример 2.1.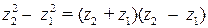 
.
Это есть известная формула разности квадратов двух чисел.
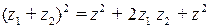
Это есть формула квадрата суммы двух чисел.
Конец примера.
Формулы умножения и деления двух комплексных чисел запоминать не следует, так как в следующем Вопросе лекции №2 будут указаны простые способы выполнения этих операций путем представления комплексного числа в одной из трех форм: алгебраической, тригонометрической и показательной.
