Розглядаються ряди, у яких два сусідніх члени ряду мають різні знаки, наприклад: 
для визначення збіжності таких рядів використовується теоремаЛейбніця:
Ряд збігається, якщо його члени монотонно спадають за абсолютною величиною і загальний член наближається до нуля при п, яке наближається до нескінченості, тобто виконуються умови:
1. послідовність абсолютних величин членів ряду монотонно спадає, тобто 
2. загальний член ряду прямує до нуля 
При цьому сума S ряду (10) задовольняє нерівності: 
.
Абсолютна збіжність ряду. коли ряд, складений з абсолютних членів ряду, у якого знаки чергуються, 
збігається, то і заданий ряд збігається абсолютно.
Умовна збіжність ряду. коли ряд, складений з абсолютних членів збіжного ряду, у якого знаки чергуються, розбігається, то заданий ряд збігається умовно.
Приклад 4.27. Дослідити збіжність ряду 
.
Розв'язання. Ряд задано у згорнутому вигляді. Представимо його в розгорнутому виді, підставляючи послідовно 
:
Ряд збігається за ознакою Лейбніця, тому що виконуються обидві її умови, а саме;
1. Абсолютні значення членів ряду монотонно спадають:
2. Загальний член ряду має границею нуль:
Перевіряємо ряд на абсолютну збіжність. ряд, складений з абсолютних членів заданого ряду
розбігається, тому що він утворений з непарних членів гармонійного ряду, який розбігається.
Тому і даний ряд збігається умовно.
 |
14.5. Степеневі ряди
Для визначення збіжності такого степеневого ряду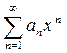 
можна використовувати узагальнену ознаку Даламбера. Знаходимо
.
Ряд збіжний при q < 1. Доведено також, що при q > 1 ряд розбіжний. Таким чином, додатковому дослідженню підлягають лише ті значення, при яких q = 1.
Якщо степеневий ряд містить лише послідовні степені, то дещо простіше використовувати формулу для радіусу збіжності, яка випливає з ознаки Даламбера: де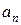 
, – коефіцієнт при загальному членові 
.
Приклад 4.28. Знайти область збіжності ряду 
Розв’язання. 
Ряд збіжний в інтервалі (-1; 1).
Розглянемо збіжність ряду на кінцях цього інтервалу.
а) 
. Отримаємо ряд 
Оскільки 
і 
, то за теоремою Лейбніця ряд збіжний.
б)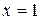 
. Отримаємо ряд 
Це гармонійний ряд, який, як відомо, розбіжний.
Отже, область збіжності даного ряду є напівінтервал [-1; 1).
Приклад 4.29. Знайти інтервал збіжності ряду: 
Розв’язання.
Знаходимо радіус збіжності
.
Ряд збіжний при 
.
При 
маємо ряд 
, який розбіжний за ознакою порівняння з гармонійним рядом.
При 
маємо ряд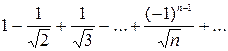 
, який збіжний за ознакою Лейбніця.
Отже область збіжності 
Приклад 4.30. Знайти область збіжності ряду: 
.
Розв’язання.
Радіус збіжності
; 
.
При х =1
Збіжність ряду перевіряємо за теоремою порівняння рядів. Оскільки в знаменнику загального члена старший степінь n рівний 2, то для порівняння візьмемо ряд, отриманий з гармонійного ряду з n в степені 2.
Відомо, що ряди, отримані з гармонійного ряду з n в степені більше 1, збіжні. Порівнюємо відповідні члени початкового і досліджуваного ряду.
.
Отже, ряд також збіжний.
При х =-1 отримаємо ряд:
Ряд збіжний за теоремою Абеля, яка стверджує, що коли збігається ряд складений з членів знакозмінного ряду, взятих із знаком плюс, то і знакозмінний ряд збіжний.
Відповідь. Область збіжності ряду [-1;1].
Формула Тейлора
