Означення. Диференціальне рівняння типу
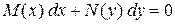 (4.7)
(4.7)
називають рівнянням із відокремленими змінними, тому що в цьому рівнянні змінні розділені, тобто при 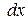 знаходиться тільки функція від х, а при
знаходиться тільки функція від х, а при  - тільки функція від у.
- тільки функція від у.
Інтегруючи обидві частини цього рівняння, одержимо співвідношення, яке пов'язує розв'язок у, незалежну змінну х і довільну сталу С, тобто одержимо загальний інтеграл рівняння
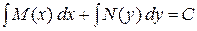 . (4.8)
. (4.8)
Приклад 4.1. Знайти загальний розв'язок рівняння 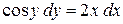 .
.
Розв'язання.
 ,
, 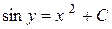 ,
, 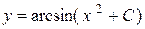 .
.
Приклад 4.2. Розв'язати рівняння 
Розв'язання.
Представляють 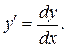
Запишемо рівняння в диференціалах 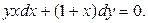
Для відокремлення змінних треба розділити кожну з частин рівняння на добуток функцій 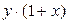 . Множник
. Множник 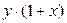 називається розділяючим множником.
називається розділяючим множником.
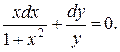
Змінні відокремлені і можна інтегрувати.
 ;
;

Отриманий розв'язок є загальним інтегралом диференціального рівняння. Можна одержати і загальний розв'язок диференціального рівняння, якщо перетворити отриманий розв'язок:
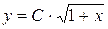 .
.
Приклад 4.3. Знайти загальний розв'язок рівняння
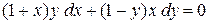 .
.
Розв'язання. Розділяючи змінні, знаходимо:
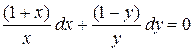 ,
,
 .
.
Інтегруючи, отримаємо:
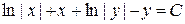 або
або 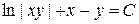 .
.
Останнє співвідношення є загальним інтегралом даного рівняння.
Приклад 4.4. Розв'язати задачу Коші
 ,
, 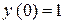 .
.
Розв'язання. Розділяючи змінні, знаходимо:
 .
.
Інтегруючи, отримаємо:
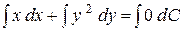 ,
,
 .
.
Одержали загальний інтеграл вихідного рівняння.
Розв'язавши останнє рівняння відносно у, знайдемо загальний розв'язок вихідного рівняння
 ,
, 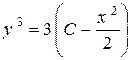 ,
, 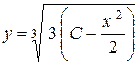 .
.
Знайдемо частинний розв'язок, який задовольняє початковій умові 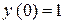 :
:
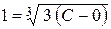 ,
,  ,
, 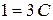 ,
,  .
.
 - розв'язок задачі Коші.
- розв'язок задачі Коші.
Однорідні диференціальні рівняння
Означення. Функція 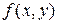 називається однорідною функцією n-го порядку щодо змінних х і у, якщо при будь-якому t справедлива тотожність
називається однорідною функцією n-го порядку щодо змінних х і у, якщо при будь-якому t справедлива тотожність
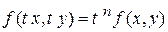 .
.
Приклад 4.5. 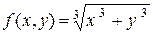 - однорідна функція першого порядку, тому що
- однорідна функція першого порядку, тому що
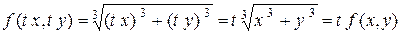 .
.
Приклад 4.6. 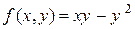 - однорідна функція другого порядку, тому що
- однорідна функція другого порядку, тому що
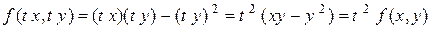 .
.
Приклад 4.7.  - однорідна функція нульового порядку, тому що
- однорідна функція нульового порядку, тому що
 .
.
Означення. Рівняння виду  називається однорідним, якщо функції при
називається однорідним, якщо функції при  і
і  є однорідними однакового порядку.
є однорідними однакового порядку.
Однорідне рівняння зводиться до вигляду  і за допомогою заміни змінних
і за допомогою заміни змінних  , де
, де 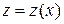 ,
, 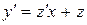 , або
, або  зводиться до рівняння із змінними, які відокремлюються.
зводиться до рівняння із змінними, які відокремлюються.
Приклад 4.8. Розв'язати задачу Коші
 ,
,  .
.
Розв'язання. 

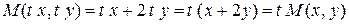
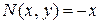
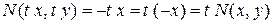
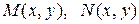 - однорідні функції першого порядку
- однорідні функції першого порядку
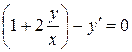

 ,
, 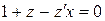 ,
, 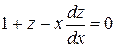 ,
,

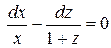 ,
,  ,
,
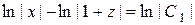 ,
,
 ,
, 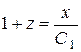 ,
, 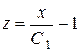 ,
, 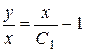 ,
,
 - загальний розв'язок.
- загальний розв'язок.
Знайдемо частинний розв'язок, який задовольняє початковій умові  :
: 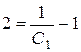 ,
, 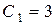 .
.
 - розв'язок задачі Коші.
- розв'язок задачі Коші.
Лінійні диференціальні рівняння
Означення. Лінійним рівнянням першого порядку називається рівняння, що має вигляд
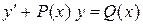 , (4.9)
, (4.9)
де 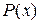 і
і 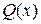 - задані неперервні функції від х (або сталі).
- задані неперервні функції від х (або сталі).
Якщо 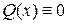 , то рівняння називається однорідним.
, то рівняння називається однорідним.
Метод Бернуллі
Шукаємо розв'язок рівняння (4.9) у вигляді добутку двох функцій від х:
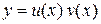 , (4.10)
, (4.10)
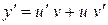 . (4.11)
. (4.11)
Підставши у і 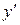 в (4.9), маємо:
в (4.9), маємо:
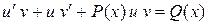 ,
, 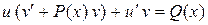 . (4.12)
. (4.12)
Виберемо функцію  такою, щоб
такою, щоб
 , (4.13)
, (4.13)
 ,
,  ,
, 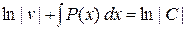 ,
,
 ,
,  ,
,
 ,
,  .
.
Так як нам досить якого-небудь відмінного від нуля розв'язку рівняння (4.13), то за функцію 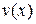 візьмемо
візьмемо  .
.
Підставляючи знайдене значення 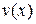 в (4.12), одержимо:
в (4.12), одержимо:
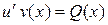 ,
, 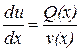 ,
, 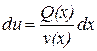 ,
, 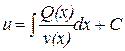 .
.
Підставляючи 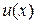 й
й 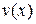 у (4.10), одержуємо розв'язок неоднорідного рівняння:
у (4.10), одержуємо розв'язок неоднорідного рівняння:
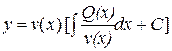 ,
,
 . (4.14)
. (4.14)
Приклад 4.9. Розв'язати рівняння
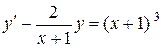 .
.
Розв'язання. 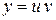 ,
, 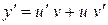 , звідки маємо:
, звідки маємо:
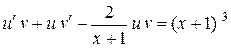 ,
, 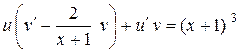 .
.
Згідно методу виберемо функцію  такою, щоб
такою, щоб 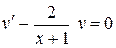 , тоді
, тоді 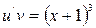 . Розв’язуємо перше рівняння
. Розв’язуємо перше рівняння
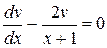 ,
, 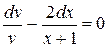 ,
, 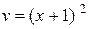 .
.
Підставляємо в друге
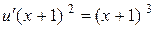 ,
,  ,
, 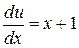 ,
,  ,
,
 .
.
Підставляючи 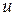 й
й  , одержуємо загальний розв'язок рівняння:
, одержуємо загальний розв'язок рівняння:
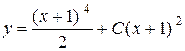 .
.
2. Метод Лагранжа (метод варіації довільної сталої)
Суть методу полягає в тому, що спочатку знаходимо загальний розв'язок відповідного лінійного однорідного рівняння 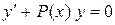
 .
.
Потім, вважаючи в цьому розв'язку сталу С функцією від х, шукаємо розв'язок лінійного неоднорідного рівняння у вигляді:
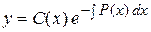 . (4.15)
. (4.15)
Розв'язок (4.15) повинен задовільняти рівняння (4.9). Диференціюючи і підставляючи (4.15) в (4.9), маємо:
 ,
,
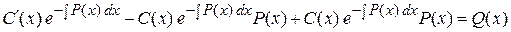 ,
,
 ,
, 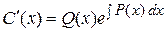 ,
,
 ,
,
 . (4.16)
. (4.16)
Він співпадає з розв'язком (4.14).
Приклад 4.10. Розв'язати рівняння методом Лагранжа
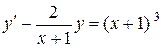 .
.
Розв'язання. Розв'яжемо відповідне однорідне рівняння
 ,
, 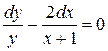 ,
, 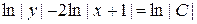
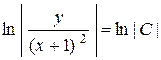 ,
,  .
.
Вважаючи в цьому розв'язку сталу С функцією від х, шукаємо розв'язок лінійного неоднорідного рівняння у вигляді:
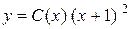 ,
, 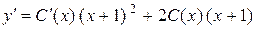 .
.
Підставимо у вихідне рівняння у, 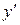 і з отриманого диференціального рівняння знайдемо функцію
і з отриманого диференціального рівняння знайдемо функцію 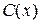 :
:
 ,
,
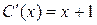 ,
,  .
.
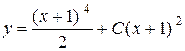 – загальний розв'язок.
– загальний розв'язок.






