Поняття генеральної та вибіркової сукупностей. Похибка репрезентативності. Обсяг вибірки

 

Найважливіша ознака вибіркового спостереження як виду несуцільного спостереження – випадковий характер вибірки, а головна його особливість полягає в тому, що при відборі одиниць сукупності для обстеження забезпечується рівна можливість попадання у відібрану частину будь-якої з одиниць. Переваги вибіркового спостереження перед суцільним спостереженням реалізуються лише при дотриманні наукових принципів його організації і проведення, тобто відповідного, насамперед неупередженого, випадкового відбору одиниць для спостереження.

Отже, вибіркова сукупність повинна повністю відтворювати склад генеральної сукупності. Саме тому при розгляді питань що стосуються вибіркової сукупності необхідно зупинитися на основних термінах вибіркового спостереження.

Генеральна сукупність – це вся сукупність одиниць, з якої проводиться відбір частини одиниць для вибіркового спостереження. Таким чином, відібрана в певний спосіб частина генеральної сукупності для вибіркового спостереження називається вибірковою сукупністю. Узагальнюючі показники генеральної сукупності називаються генеральними, а відповідні показники вибіркової сукупності – вибірковими. Водночас принцип випадковості відбору забезпечує всім одиницям генеральної сукупності рівні можливості потрапити у вибіркову сукупність.

Таким чином генеральна сукупність (N) це сукупність одиниць, з якої проводиться відбір деякої їх частини для статистичного дослідження. А вибіркова сукупність (n) це сукупність одиниць, яка відібрана з генеральної сукупності і піддана спостереженню (реєстрації ознак що цікавлять дослідника).

Генеральна сукупність (а слідом за нею і вибіркова сукупність) може бути кількісною або якісною, що залежить від того, чи є ознаки, властивості одиниць спостереження кількісними (вік) або якісними (стать). Ця відмінність припускає, що статистичний опис сукупності приймає або форму середніх арифметичних, або форму питомої ваги (частки). Тим самим, абсолютно природно, що між цими показниками генеральної і вибіркової сукупностей є якась відмінність, інакше кажучи, існує помилка у визначенні показників вибіркової сукупності саме тому, що остання є частиною генеральної сукупності. Отже, ці так звані похибки репрезентативності є розбіжністю між показниками вибіркової і генеральної сукупності. Відповідно, наголошуючи що частина завжди відрізняється від цілого і має певні відмінності, а самі ті що є між показниками генеральної і вибіркової сукупностей, в статистиці називають похибками репрезентативності. Відповідно вони пояснюються тим, що вибіркова сукупність не зовсім точно відображає склад генеральної сукупності. Таким чином, середня в генеральній сукупності відрізняється від середньої у вибірковій сукупності на величину похибки репрезентативності. Похибки репрезентативності можуть бути систематичними і випадковими. Якщо перші виникають у зв'язку з особливостями прийнятої системи відбору і обробки даних спостережень або у зв'язку з порушенням встановлених правил відбору, то другі в наслідок недостатньо рівномірного уявлення у вибірці окремих видів одиниць генеральної сукупності.

Наприклад, генеральна сукупність правопорушників складається з 500 осіб. З них 30% складають злочинці, які виховувались в неповних сім’ях. При вибірковому спостереженні було вивчено 50 правопорушників, серед яких питома вага таких осіб склала 25%. Помилка вибірки дорівнює 30-25=5%. Середня арифметична величина віку злочинців в генеральній сукупності склала 28,3 роки, а у вибірковій сукупності – 26,5 років, що дає похибку яка дорівнює 28,3-26,5=1,8 років.

В загальному вигляді формула для розрахунку похибки репрезентативності така:

, (1)

 

де ² – дисперсія; – середнє квадратичне відхилення (СКВ);

n – число одиниць вибірки.

Аналіз формули (1) показує, що похибка репрезентативності прямо пропорційна та зворотно пропорційна числу одиниць вибірки n, тобто w буде тим менше, чим менше дисперсія (СКВ) і чим більше n. Якщо статистичне дослідження вже проведено, тобто обсяг вибірки n вже відомий, завданням буде розрахунок дисперсії. Для якісних ознак дисперсія (СКВ) розраховується за формулою:

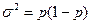(2)

де р – частка якісної ознаки; 1 – р – частка інших ознак (протилежних ознак).

Для вищенаведеного прикладу р = 30% = 0,3; ² = 0,3 (1-0,3) = 0,21;

Для кількісних ознак

, (3)

де: х₁,х₂, …, х_і, …,х_n – показник варіюючої ознаки, - середнє арифметичне значення ознаки, а f_1, f_2, f_3, …f_i, …, f_n - частоти варіюючої ознаки.

З врахуванням вищенаведених формул (2) та (3), формули для розрахунку похибок репрезентативності якісних і кількісних ознак матимуть наступний вигляд:

, (4)

(5)

Розглянемо приклад розрахунку похибки репрезентативності (w) для статистичної вибірки 100 засуджених (n=100), що відбувають покарання строком від одного до шести років. Розподіл засуджених за строками ув’язнення приведено в таблиці.

Таблиця. Розподілу засуджених за строками ув’язнення.

Строк, років
Засуджених, осіб

 

Середня арифметична строку ув’язнення дорівнює:

Дисперсія:

Похибка репрезентативності:

Якщо обсяг вибірки збільшити в чотири рази, тобто до 400 засуджених, то похибка репрезентативності може бути зменшена вдвічі, що складатиме року.

Формули (4) та (5) доцільні для так званої повторної вибірки, коли кожна відібрана одиниця знову повертається в загальний масив сукупності.

При безповторному відборі, коли кожна відібрана одиниця виключається з числа одиниць генеральної сукупності (відібрана одиниця може потрапити в вибірку лише один раз), похибка вибірки для якісних та кількісних розраховується по таким формулам:

, (6)

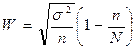(7)

Наявність множника у формулах (6) і (7) дозволяє більш точно вирахувати помилку безповторної вибірки, причому в бік її мінімізації. Тому якщо досліднику невідома чисельність генеральної сукупності, а ним здійснена безповторна вибірка, то похибка репрезентативності може бути вирахувана за формулою повторної вибірки. Незначну неточність, що пов’язана зі збільшенням розрахункової помилки, можна не враховувати, оскільки соціально-правові дослідження не потребують високої точності.

Гранична похибка репрезентативності знаходиться як добуток однократної помилки вибірки на відповідний коефіцієнт довіри t:

= wt (8)

Коефіцієнт довіри (коефіцієнт кратності похибки) t дозволяє збільшити репрезентативність вибірки за рахунок збільшення вибіркової сукупності. Для кримінологічних, соціально-правових досліджень, а також для практичних оперативних цілей дозволяється точність з коефіцієнтом довіри t=1. При рішенні важливих наукових та практичних питань бажано щоб t=2. Значення t>2 при визначені крайньої похибки репрезентативності в юридичній статистиці майже не використовується.

Визначення обсягу вибіркової сукупності має суттєве значення для дослідників. Кількість одиниць сукупності, що відбираються для вибіркового спостереження, має бути досить велика. Водночас, кількість одиниць, відібраних для вибіркового спостереження завжди залежить від того наскільки однорідна чи різнорідна сукупність. Якщо сукупність однорідна, тим менше одиниць відбирається, і навпаки, чим різнорідніша сукупність тим більше одиниць необхідно відібрати. Необхідно врахувати й те, що чим менше одиниць відбирається для спостереження тим більше може бути похибка репрезентативності. Так і в тому разі, якщо для вибіркового спостереження відбирається дуже значна кількість одиниць, то відбувається зайва витрата часу на його проведення, що призводить до нівелювання основного змісту та цілей вибіркового спостереження. Беззаперечно, що основний зміст вибіркового спостереження полягає у можливості значно швидше і з найменшими витратами часу отримати необхідні результати.

Водночас, розрахунок обсягу вибіркової сукупності здійснюється на основі так званих завданих та наявних показників. Завданими показниками є гранична похибка репрезентативності (w або ), коефіцієнт довіри t, а наявними дисперсія (СКВ ) досліджуваних ознак і в деяких випадках чисельність генеральної сукупності.

Формули розрахунку вибіркової сукупності отримуються з формул розрахунку похибок репрезентативності. 1, 4-8.

Для якісних та кількісних ознак розрахунок обсягів вибіркової сукупності здійснюється за наступними формулами:

(9)

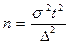(10)

Формули розрахунку обсягу вибіркової сукупності при без повторній вибірці відповідно для якісних та кількісних ознак має наступний вигляд:

(11)

(12)

Враховуючи те, що основним завданням при проведенні вибіркового дослідження у правовій статистиці є визначення репрезентативного обсягу вибіркового спостереження, тобто скільки необхідно проаналізувати одиниць з генеральної сукупності, щоб одержана випадкова похибка середнього значення досліджуваної ознаки не перевищувала визначеної величини похибки репрезентативності з достатньою імовірністю. Отже, визначення величини похибки середнього значення ознаки для встановлення обсягу вибірки є досить важливим моментом.

Визначення можливої і фактично допущеної помилки вибірки має значну роль в рішенні питання про можливість застосування вибіркового методу. Величина помилки характеризує ступінь надійності результатів вибірки, а тому знання цієї величини необхідне при оцінці параметрів генеральної сукупності. Оцінка можливої величини і складу помилок репрезентативності лягають в основу планування проектованого вибіркового спостереження.

При проведенні вибіркового спостереження необхідно враховувати наступні обставини, що обумовлюють величину випадкової помилки репрезентативності, а саме, спосіб формування вибіркової сукупності; ступінь коливання ознаки, що вивчається, в генеральній сукупності та об’єм (обсяг) вибірки. Зрозуміло, що збільшення розміру вибірки за інших рівних умов дає велику впевненість (чим більше одиниць потрапляє у вибірку, тим меншою буде можлива помилка), але оскільки потрібна можливо менша вибірка, в статистці виробляються способи, які або забезпечують підвищення точності оцінок при фіксованому розмірі вибірки, або дозволяють зменшити розмір вибірки, що вимагається для отримання заданої точності.

Враховуючи вищезазначене, підкреслимо, що похибка репрезентативності залежить від багатьох чинників: по-перше, імовірності, з якою ми бажаємо отримати результат; по-друге, кількості одиниць вибіркової сукупності; по-третє, однорідності досліджуваної сукупності, і по-четверте, від способу відбору одиниць у вибіркову сукупність.