Кількість кримінальних справ та слідчих територіального

Відділу внутрішніх справ

 

Кількість кримінальних справ, що знаходяться у провадженні у слідчих МРВВС, (х)	Кількість слідчих МРВВС, (f)	(х f) (сума кримінальних справ відносно кількості слідчих МРВВС)
100 разом

 

Обчислимо середнє навантаження на одного слідчого:

Для інтервальних варіаційних рядів розподілу, в яких значення ознаки показано в межах «від - до», середню арифметичну зважену знаходять таким чином: Спочатку необхідно інтервальний ряд розподілу перетворити в дискретний. Для цього по кожному інтервалу знаходять його середину. Серединне значення інтервалу визначають як півсуму його нижньої і верхньої меж.

Якщо мають місце інтервали з нечітко визначеними межами (відкритими) межами, де перший варіант – «до», а останній – «понад», то для визначення середнього значення потрібно встановити умовні межі цих інтервалів. Для першого інтервалу беруть величину другого інтервалу, а для останнього величину передостаннього інтервалу.

Зазначимо перехід від інтервалів з відкритими межами до інтервалів із закритими межами на прикладі розподілу областей держави за кількістю вчинених за добу тяжких злочинів:

 

Відкриті інтервали		Закриті інтервали
До 55 55-60 60-65 65-70 Понад 70		50-55 55-60 60-65 65-70 70-75

 

Після того як знайдені середини інтервалів, середню арифметичну зважену обчислюють так, як і в дискретному ряду розподілу: значення варіант множать на частоти і одержану суму добутків ділять на суму частот.

Покажемо розрахунок середньої арифметичної величини на прикладі інтервального варіаційного ряду (табл. 2.3):

Таблиця 2.3. Розрахунок середнього розміру збитку від злочину (дані умовні)

 

Розмір збитку, тис. грн.	Число злочинів	Середнє значення інтервалів	Середній розмір збитку від злочину виходячи із середнього значення інтервалу (тис. грн.)
8-10		(8 + 10): 2 = 9	9:6 = 1,5
10-12		(10+12): 2=11	11х8 = 1,4
12-14		(12+14): 2= 13	13х15=0,9
14-16		(14+ 16): 2=15	15х15 = 1
16-18		(16+18): 2 = 17	17х10=1,7

 

Для числення середньої арифметичної величини інтервального ряду потрібно перш за все одержати середину інтервалу кожної групи (див. розрахунок в табл. 2.3).

Необхідно пам'ятати, що середня арифметична інтервального ряду менш точна, чим середня арифметична, обчислена з конкретних варіантів, тому що при численні центрів-інтервалів допущена деяка умовність. Передбачається, що значення ознаки xt усередині інтервалу розподілені рівномірно.

Середня арифметична величина є одним з найважливіших узагальнюючих показників в статистиці, якій притаманні такі властивості:

1. Сума всіх позитивних і негативних відхилень варіант від середньої арифметичної дорівнює нулю:

2. Сума квадратів відхилень варіант від середньої арифметичної величини завжди менше, ніж сума квадратів відхилень варіант від будь-якого іншого числа:

3. Якщо кожну варіанту сукупності помножити або розділити на деяке постійне число А, то середня арифметична збільшиться або зменшиться в стільки ж разів:

4. Якщо до кожної варіанті сукупності додати або з кожної варіанти відняти деяке постійне число А, то середня арифметична збільшиться або зменшиться на ту ж величину:

5. Якщо збільшити або зменшити частоту кожної варіанти совокупности/в А раз, то величина середньою арифметичною не зміниться:

Середнє арифметичне розраховується по різному в дискретних і інтервальних варіаційних рядах.

У дискретних рядах варіанти ознаки умножаються на частоти, ці твори підсумовуються і одержана сума творів ділиться на суму частот.

У інтервальних рядах значення ознаки задане, як відомо, у вигляді інтервалів, тому, перш ніж розраховувати середню арифметичну, потрібно перейти від інтервального ряду до дискретного.

Як варіанти Xi використовується середина відповідних інтервалів. Вони визначаються як напівсума нижньої і верхньої меж.

Якщо у інтервалу відсутня нижня межа, то його середина визначається як різниця між верхньою межею і половиною величини наступних інтервалів. За відсутності верхніх меж, середина інтервалу визначається як сума нижньої межі і половини величини попереднього інтервалу. Після переходу до дискретного ряду подальші обчислення відбуваються по методиці розглянутої вище.

Якщо ваги fi задані не в абсолютних показниках, а у відносних, то формула розрахунку середній арифметичній буде наступною:

P_i - відносні величини структури, що показують, який відсоток складають частоти варіантів в сумі всіх частот.

Якщо відносні величини структури задані не у відсотках, а в долях, то середнє арифметичне буде обчислюватися за формулою:

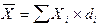
Середня геометрична. Середню геометричну застосовують, коли загаль­ний обсяг явища є не сума, а добуток значень ознаки. Ця середня викорис­товується здебільшого для розрахунку середніх коефіцієнтів (темпів) зрос­тання і приросту при вивченні динаміки явищ і має такий вигляд:

Де п – число коефіцієнтів зростання;

У_{1 і} У _{п -} - початковий і кінцевий рівні динамічного ряду.

Величина середньої геометричної залежить тільки від співвідношення кінцевого і початкового рівнів. Якщо не змінюються в цих межах інші рівні, величина середньої не зміниться. Крім того, вона застосовується для узагальнення ознак, виражених лінійними мірами яких-небудь площ (при обчисленні середніх діаметрів стовбурів дерев, кошиків, листків, клубнів тощо).

Крім розглянутих видів середніх величин у статистиці використовуються й інші середні.

Середня хронологічна являє собою середню величину з показників, що змінюються у часі і є первісною формулою середньої арифметичної. Вона розраховується за принципом середньої арифметичної простої і зваженої. Середня гармонійна проста:

Середня гармонійна зважена:

Wi – результат ділення варіантів на частоти

Також як і арифметична, середня гармонійна може бути простою та змішаною.

Для виявлення тенденції зміни досліджуваного явища у часі розраховують середню ковзну. Суть способу її розрахунку полягає в тому, що склад періоду безперервно і постійно змінюється – відбувається зсув на одну дату при збереженні постійного інтервалу (триріччя, п’ятиріччя, десятиріччя)[21].

В аналізі і плануванні, наприклад, заходів протидії злочинності застосовують середню прогресивну. Цей вид середньої дає узагальнену характеристику не всієї сукупності, а тільки тієї її частини, яка представлена показниками вищими за загальну середню.

З існуючих варіант обчислюють загальну середню. Потім відбираються варіанти, які за величиною перевищують загальну середню і за відібраними варіантами обчислюють середню, яка має назву середньої прогресивної.

Формула середньої прогресивної буде мати такий вигляд

де х₁+х₂+ х₅ – сукупність представлена числами, а х – середнє значення.

Особливими видом середніх величин є середня багатовимірна, яка являє собою середню величину кількох ознак для однієї одиниці сукупності. Так як неможливо розрахувати середню величину за абсолютними значеннями різних ознак (виражених у різних одиницях), то багатовимірна середня визначається з відносних величин (відсотках або частках), як правило, з відношень абсолютного значення суми одиниць сукупності до середніх значень цих одиниць.

Багатовимірні середні дають узагальнену характеристику кожної одиниці сукупності за кількома ознаками одночасно.

Середню багатовимірну використовують для аналізу діяльності правоохоронних органів (міськрайвідділів, прокуратур, судів), зокрема при визначенні ефективності використання наявних сил і засобів (особового складу, транспорту, засобів зв’язку, технічних засобів захисту тощо).

Середня квадратична. Використовується, як правило, для розрахунку показників варіації (зміни), які обчислюються на основі квадратів відхилень індивідуальних значень від їхньої середньої арифметичної. Крім того, вона застосовується для узагальнення ознак, виражених лінійними мірами будь-яких площ або діаметрів (полів, озер, стовбурів чи листків дерев тощо).