Види середніх величин та способи їх обчислення

У статистиці застосовуються різні види середніх величин: середня арифметична, середня гармонійна, середня геометрична.

Крім вищезазначених на практиці використовують ще й такі види середніх величин як: середня хронологічна, середня прогресивна, середня багатовимірна, середня ковзна, а також середні структурні: мода, медіана.

Будь-яку з вищезазначених середніх можна визначити як просту (коли значення варіант спостерігається один раз або однакову кількість разів) і як зважений, коли значення варіант повторюється декілька разів.

Уведемо такі позначення і поняття середніх:

х - середнє значення досліджуваної ознаки;

х - окремі значення усереднюваної ознаки (варіанти);

п - число одиниць досліджуваної сукупності;

/- частота повторень (вага) варіант;

W = xf- обсяг явищ.

Ознаку за якою знаходять середню називають усередненою ознакою. Величину ознаки кожної окремої одиниці сукупності називають варіантою, або значенням досліджуваної ознаки. Частоту повторень варіантів у сукупності (наприклад, загальній кількості вчинених злочинів) називають статистичною вагою.

Середні величини, що застосовуються в статистиці, належать до за­
гального типу степеневих середніх. Відрізняються вони тільки показником
степеня. Математична статистика виводить різні середні з формули степе­
невої середньої, яка являє собою корінь к-то степеня з частки від ділення
суми індивідуальних значень ознаки к-го степеня на число індивідуальних
значень:

Вибір того чи іншого виду середньої визначається цілями і завдання­ми дослідження і наявною інформацією.

Загальною умовою правильного обчислення усіх видів середніх є збе­реження незмінним загального обсягу варіюючої ознаки при заміні інди­відуальних значень ознаками їхньої середньої. Так, середня арифметична застосовується тоді, коли обсяг варіюючої ознаки утворюється як сума окремих варіант; середня гармонічна - коли обсяг варіюючої ознаки утво­рюється як сума обернених значень окремих варіант; середня геометрична -коли обсяг варіюючої ознаки утворюється як добуток окремих варіант; середня квадратична - коли обсяг варіюючої ознаки утворюється як сума квадратів окремих варіант.

Розглянемо перелічені вище види середніх величин більш докладно.

Найбільш поширеним видом середніх величин в статистиці є середня арифметична, що є результатом ділення суми індивідуальних значень ознак на їх кількість. Середня арифметична величина буває простою і зваженою.

Середня арифметична проста являє собою частку від ділення суми індивідуальних значень ознаки на їх загальне число. її обчислюють за формулою

Середня арифметична проста застосовується в тих випадках, коли відомі дані про окремі значення ознаки та їх число в сукупності. В статис­тичній практиці вона застосовується, як правило, для розрахунку середніх рівнів ознак, наданих у вигляді абсолютних показників.

Для з'ясування методики розрахунку середньою арифметичною використовуємо наступні позначення:

X - арифметична ознака

X (X1, X2,... X3) - варіанти певної ознаки

n - число одиниць сукупності

- середня величина ознаки

Залежно від початкових даних середня арифметична може бути розрахована двома способами:

1. Якщо дані статистичного спостереження не згруповані, або згруповані варіанти мають однакові частоти, то розраховується середня арифметична проста:

Допустимо, що кількість правопорушень по 10 населеним пунктам регіону за звітний період склало: 3100, 3600, 4500, 4900, 5300, 5400, 5600, 5700, 5900, 6000. Стан злочинності одного населеного пункту саме по собі не може дати уявлення про її рівень по всьому регіону. Для цього треба визначити середній рівень злочинності. Його в даному прикладі можна визначити так: підсумовуємо стан злочинності по всіх населених пунктах і одержаний підсумок розділимо на число населених пунктів в обстежуваному регіоні. Це дасть наступне рівняння:

 

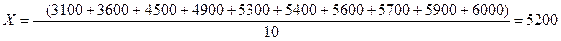
Тобто середньорічний рівень злочинності по регіону складає 5200 злочинів. Це проста середня арифметична величина. Простою вона називається тому, що обчислюється простим підсумовуванням індивідуальних значень ознаки і діленням цієї суми на число значень. В статистичній практиці вона застосовується, як правило, для розрахунку середніх рівнів ознак наданих у вигляді абсолютних показників.

2. Якщо згруповані варіанти в даних мають різні частини, то розраховується середня арифметична зважена:

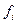- чисельність (частоти) варіантів

- сума частот

Для прикладу середньої зваженої візьмемо дані про стан злочинності в різних населених пунктах, у табл. 2.1

Таблиця 2. 1

Стан злочинності по населених пунктах регіону (дані умовні)

Населені пункти регіону
Пункти
Назва пунктів	Пункт А.	Пункт Б.	Пункт С.	Пункт Д.	Пункт Е.
Кількість вчинених злочинів
Кількість населених пунктів, в яких повторюються (співпадає) кількість злочинних проявів

 

У даному прикладі тільки в двох населених пунктах стан злочинності за даний період склав 2700 епізодів, в чотирьох - 2000 і т.і., тобто кожен варіант повторюється неоднакове число разів. Тому при обчисленні середнього рівня злочинності не можна користуватися формулою середньої арифметичної простій. Щоб визначити рівень злочинності по досліджуваних населених пунктах, спочатку треба визначити загальний стан злочинності для всіх населених пунктів. Для цього помножують по кожній групі кількість злочинів на число населених пунктів і одержані дані підсумовують. Середній рівень злочинності по всій сукупності населених пунктів визначається діленням одержаної суми на число населених пунктів. У нашому прикладі частотами є 2, 3, 4, 5, 6. Вони показують, що кількість злочинів, що дорівнює 2700 фактам, зустрічається в 2 населених пунктах, тобто 2 рази, 2000 - 4 рази тощо. Частоти ще називають вагами середньої величини, звідси і відбувається назва середньої зваженої.

Позначивши умовно частоти літерою Х, розрахунок середній арифметичній зваженій можна виразити наступною формулою:

- середнє значення досліджуваної ознаки (варіанти)

Xf – обсяг явищ

f – частота повторень варіант

Таким чином, при численні середньої арифметичної зваженої величини необхідно всі значення варіант помножити на їхню частоту, одержані рівняння підсумувати і цю суму розділити на суму частот, тобто загальний обсяг сукупності.

Частоти f називають вагою, а множення варіантів Х на частоти - зважуванням. Замість частот можливе застосування часток d. Тоді форма середньоарифметичної зваженої буде виглядати таким чином:

= x₁d₁+x₂d₂+x₃d₃+ … +x_md_m=

Середня арифметична має певні властивості, найсуттєвішими з яких є:

1) сума відхилень усіх значень правової ознаки від середнього її значення дорівнює 0;

2) добуток середнього значення дорівнює сумі індивідуальних значень ознаки, тобто загальному обсягу цієї ознаки;

3) сума квадратів відхилень кожного значень ознаки від середньої величини завжди менша за будь-яку величину[19].

Якщо частоти різні, то розрахунок середньої величини роблять за середньою арифметичною зваженою[20].

Середня називається арифметичною зваженою, тому що визначається з урахуванням питомої ваги окремих значень ознаки загальної сукупності (х f)

Розглядаючи формули середньої арифметичної зваженої можна помітити, що вона майже не має відміни від простої середньої арифметичної. В ній підсумовування f (кількість) разів одного і того ж самого варіанта (х) замінюють множенням його на число повторень (частоту - f).

Покажемо це на прикладі (таб. 2.1)

Таблиця 2.2