В продажу поступило 40% телевизоров с первого завода, 50% - со второго, 10% - с третьего. Вероятность того, что телевизор, изготовленный на первом заводе, имеет дефект, равна 0,1. Для телевизоров, изготовленных на втором и третьем заводах, эти вероятности соответственно равны 0,15 и 0,2. 1) Какова вероятность приобрести исправный телевизор? 2) Приобретен исправный телевизор. Найти вероятность того, что он поступил с первого завода.
Решение.
1). Пусть событие 
. Это событие может произойти с одной из следующих гипотез: 
, 
,
.
Из условия задачи вероятности гипотез равны:
; 
; 
.
При этом должно выполняться равенство 
, что действительно так: 0,4+0,5+0,1=1.
Вычислим условные вероятности
.
Аналогично 
и 
.
Вероятность того, что наудачу купленный телевизор без дефекта, по формуле полной вероятности равна 
= 
+ 
+ 
=
= 
.
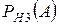2) Пересчитаем вероятность гипотезы , если известно, что событие произошло, т.е. найдем условную вероятность 
.
По формуле Байеса = 
.
Решения заданий типа 171-180.
Непрерывная СВ Х задана функцией распределения 
= 
Найти:
1) коэффициент А;
2) плотность распределения вероятностей 
;
3) математическое ожидание СВ Х;
4) вероятность события 
.
Решение. 1). Из непрерывности функции распределения и свойства 
следует, что 
. Откуда 
.
2). Плотность распределения вероятностей найдем из формулы = 
:
= 
3). Математическое ожидание 
непрерывной СВ определяется формулой = 
. Так как функция задана тремя различными выражениями на трех интервалах, то несобственный интеграл разобьется на сумму трех интегралов:
= 
+ 
+ 
= 
= 
= 
.
4). Вероятность события 
найдем по формуле 
. В нашем случае 
и поэтому 
.
Задание задания типа 181-190.
Зависимость выпуска валовой продукции (с.в. Y) от стоимости основных фондов (с.в. Х) 50 предприятий представлена корреляционной таблицей
| X Y | 0,3 | 0,9 | 1,5 | 2,1 | 2,7 | mi |
| 0,6 | ||||||
| 1,8 | ||||||
| 3,0 | ||||||
| 4,2 | ||||||
| 5,4 | ||||||
| mj | n = 50 |
В первом столбце таблицы указаны наблюдаемые значения с.в. Х (xi), в последнем столбце – соответствующие частоты наблюдаемых значений (mi). В первой строке таблицы указаны наблюдаемые значения с.в. Y (yj), в последней строке – соответствующие частоты (mj) появление этих значений. На пересечении строк и столбцов таблицы указаны частоты (mij) появления пары (xi, yj).
Требуется:
1. Найти уравнение прямой линии регрессии Y на Х.
2. Найти уравнение прямой линии регрессии Х на Y.
3. Построить графики полученных прямых.
4. Оценить тесноту корреляционной связи, используя выборочный коэффициент корреляции.
Решение.
1. Эмпирическую линейную функцию регрессии Y на Х ищем в виде
Используя метод наименьших квадратов, получим расчетные формулы для определения неизвестных параметров а и b, а именно, систему двух уравнений с двумя неизвестными:
где выборочные средние 
и 
вычисляются по формулам:
, 
, 
, 
.
В нашем случае
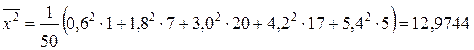
5,7528
Подставив данные значения в систему уравнений, получим
Решая систему, получим оценки параметров 
и 
Окончательный вид уравнения регрессии Y на Х: 
.
2. Уравнение прямой линии регрессии Х на Y ищем в виде 
, где числовые параметры с и d найдем из системы
.
Выборочное среднее 
вычислим по формуле = 
, а именно
= 
Подставив значения и в систему, получим:
Откуда 
и 
.
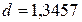Окончательный вид уравнения регрессии Х на Y: 
.
3. Построим графики найденных прямых регрессий.
4. Определим выборочный коэффициент корреляции 
по формуле
,
где выборочные средние квадратические отклонения 
и 
вычисляются по формулам = 
, = 
.
В нашем случае = 
, = 
. Тогда 
.
На практике теснота корреляционной связи оценивается по значению коэффициента следующим образом:
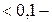пренебрежимо малая;
слабая;
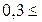
существенная;
большая;
очень большая, близкая к функциональной.
Так как в нашем случае = 
, то теснота связи между случайными величинами Х и Y большая.
