Теоретический справочник
При вычислении пределов используются следующие свойства пределов:
, где 
, т.е. предел постоянной равен самой постоянной.
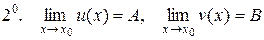, то
а) 
;
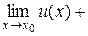
б) 
;
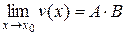в) 
, если 
.
Из свойств 10 и 
следует, что
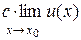, где , т.е. постоянную можно выносить за знак предела.
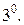Если 
, то 
.
Если 
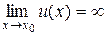, то 
.
.
Для всех элементарных функций 
в любой точке их области определения имеет место равенство: 
, т.е. предел функции находят непосредственной подстановкой предельного значения аргумента.
Из свойства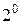 
следует, что предел суммы, произведения, частного двух функций равен, соответственно, сумме, произведению и частному пределов этих функций, если функции имеют конечные пределы (в случае частного предел знаменателя не равен нулю). Если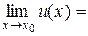 
, то 
приводит к неопределенности типа 
; если 
, то приводит к неопределенности типа 
; если 
, то 
приводит к неопределенности типа 
. Чтобы вычислить такие пределы, т.е. «раскрыть неопределенность», необходимо провести дополнительные преобразования.
Пример 1. Вычислить предел 
.
Числитель и знаменатель дроби являются многочленами и при 
стремятся к бесконечности и, следовательно, имеем неопределенность . Для раскрытия такой неопределенности вынесем в числителе и знаменателе 
.
= 
=
= 
=
= 
.
Рассмотрим случай, когда многочлен, стоящий в числителе имеет меньшую степень по сравнению с многочленом, стоящим в знаменателе:
= 
.
Рассмотрим случай, когда многочлен, стоящий в числителе имеет большую степень по сравнению с многочленом, стоящим в знаменателе:
= 
.
Пример 2. Вычислить 
.
Определим, имеет ли место неопределенность. Для этого в выражение, стоящее под пределом подставим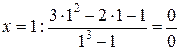 
. Т.о. имеем неопределенность . Разложим на множители числитель: 
= 
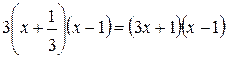, знаменатель: 
и подставим это в предел 
= 
= 
= 
.
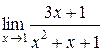Пример 3. Вычислить 
.
= 
. Домножим числитель и знаменатель на выражение сопряженное числителю: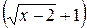 
.
= 
.
Если при раскрытии неопределенности , дробь содержит тригонометрические функции, то в этом случае используют первый замечательный предел: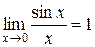 
.
Пример 4. Вычислить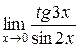 
.
= 
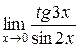. Преобразуем выражение
= 
. Отдельно вычислим: 
=
= 
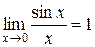= . Аналогично, 
= 
=
= 
= 
= 
. 
.
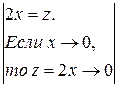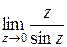Следовательно, =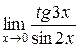 
= 
.
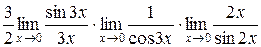Пример 5.
= 
=
= 
= 
=
= 
.
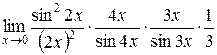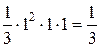При раскрытии неопределенности 
используют второй замечательный предел: 
или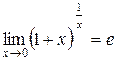 
.
Пример 6. Вычислить 
.
Вычислим отдельно предел основания 
= 
=
= 
= 
и предел показателя 
, получаем неопределенность .
Преобразуем выражение в скобках к виду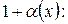 
, т.е. 
. Из второго замечательного предела следует, что 
, поэтому преобразуем показатель степени так, чтобы он содержал сомножитель 
Таким образом 
= 
. Тогда 
= 
= 
=
= 
= 
= 
.
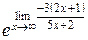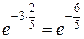Пример 7. Вычислить 
.
Выражение в скобках запишем в виде 
т.е.
. Следовательно, показатель степени должен содержать сомножитель 
:
= 
=
= 
= 
.
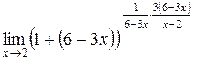Для раскрытия неопределенностей типа или удобно использовать правило Лопиталя-Бернулли: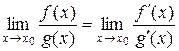 
, т.е. предел отношения функций в случае неопределенности или равен пределу отношения производных этих функций.
Для применения правила Лопиталя-Бернулли необходимо научиться вычислять производные функций.
Пример 8. Вычислить 
.
= 
.
Правило Лопиталя-Бернулли при вычислении предела можно применять несколько раз.
Пример 9. Вычислить 
.
= 
=
= 
= 
.
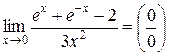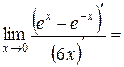
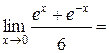
