Теоретический справочник.
Дифференциальным уравнением I-го порядка называется уравнение, связывающее независимую переменную х, искомую функцию 
и ее производную 
, т.е. уравнение вида
или 
.
Общим решением дифференциального уравнения называется такая функция 
, 
, определенная и непрерывно дифференцируемая в интервале 
, которая обращает данное уравнение в тождество, т.е.
.
Частным решением дифференциального уравнения называется решение, получаемое из общего при конкретном значении произвольной постоянной с, которую можно определить из условия 
, называемое начальным условием.
Чтобы решить дифференциальное уравнение I-го порядка, нужно определить его вид, найти его общее решение, а затем частное решение.
Пример 1. Найти частное решение дифференциального уравнения I порядка
, удовлетворяющее начальному условию 
.
Решение. Преобразуем исходное уравнение, разделив обе его части на 
:
или 
. Затем разделим обе части уравнения на 
: 
. Разделив правую часть уравнения (и числитель, и знаменатель) на 
, получим 
однородное дифференциальное уравнение I порядка, т.к. оно имеет вид 
. Сделаем замену переменной: 
. Тогда исходное уравнение примет вид 
или 
или 
. Пользуясь свойством пропорции, соберем возле дифференциалов соответствующие переменные: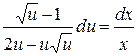 
и проинтегрируем полученное равенство: 
. Найдем интеграл, стоящий слева: 
= 
=
= 
= 
= 
.
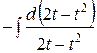
Найдем интеграл, стоящий справа: 
. Следовательно, 
, или, возвращаясь к прежним переменным и обозначая 
, получим 
. Преобразуем последнее равенство, используя свойство логарифма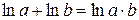 
, и получим общее решение 
. Подставив в последнее соотношение начальное условие 
, найдем конкретное значение произвольной постоянной: 
или 
. Тогда частное решение примет вид 
или 
.
Ответ:
Пример 2. Найти частное решение дифференциального уравнения I порядка
, удовлетворяющее начальному условию 
.
Решение. Разделим обе части уравнения на 
:
или 
.
Данное уравнение является линейным, т.к. имеет вид 
и решается заменой 
, где 
неизвестные функции;
.
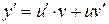Подставляя выражения для 
в исходное уравнение, получим
. Сгруппируем слагаемые, содержащие функцию 
: 
. В качестве функции 
выбирают одну из функций, удовлетворяющих уравнению 
или 
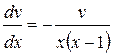. Интегрируем последнее соотношение, разделяя переменные: 
или 
, 
, 
, 
. Тогда функция определится из уравнения 
. Подставляя найденную функцию 
, получим 
или 
или 
. Интегрируя последнее уравнение, найдем функцию 
: 
. Итак, общее решение имеет вид или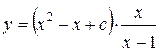 
. Подставляя начальные данные 
, получаем уравнение: 
откуда . Частное решение имеет вид 
.
