При условном делении экономики на три отрасли задана матрица коэффициентов прямых затрат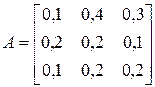 
и вектор конечной продукции 
. Требуется:
1. Записать уравнение линейного межотраслевого баланса в координатной форме.
2. Найти плановые объемы выпуска валовой продукции отраслей. Систему линейных алгебраических уравнений решить методом Гаусса. Решение системы записать в неправильных дробях.
3. Выполнить проверку результата.
4. Записать приближенный ответ с точностью до сотых.
1. Уравнение линейного межотраслевого баланса имеет вид 
, где 
вектор валового выпуска продукции, 
вектор конечного потребления, 
матрица прямых материальных затрат. Известны вектор конечного потребления и матрица прямых материальных затрат .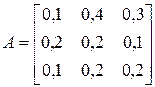
Подставим в уравнение Леонтьева векторы 
и матрицу А:
.
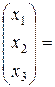
Используя правила умножения матриц, сложения векторов и определение равенства векторов, получаем систему уравнений:
Полученная система – это векторное уравнение линейного межотраслевого баланса в координатной форме.
Для решения этой системы приведем подобные члены:
Все уравнения умножим на 10:
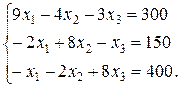
2. Решим полученную систему методом Гаусса. Основная его идея состоит в том, что данная система линейных уравнений преобразуется в равносильную ей систему специального вида, где одно из уравнений содержит все неизвестные, второе – на одно неизвестное меньше, и т.д., последнее уравнение содержит лишь одно из неизвестных. Эти преобразования называют прямым ходом метода Гаусса.
Для удобства вычислений третье уравнение поставим первым, и оно будет ведущим на первом этапе вычислений:
Исключим неизвестную 
из второго уравнения. Для этого умножим первое уравнение на 9 и прибавим ко второму:
.
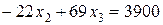Исключим неизвестную из третьего уравнения. Для этого умножим первое уравнение на (–2) и прибавим к третьему:
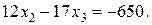
Получаем систему:
Исключим неизвестную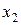 
из третьего уравнения. Для этого второе уравнение разделим на 22, умножим на 12 и прибавим к третьему:
или 454 х 3 = 32500 или 227 х 3 = 16250.
Получаем систему:
Замечание.
Преобразования в методе Гаусса удобнее выполнять не с самой системой уравнений, а с расширенной матрицей системы, которая состоит из коэффициентов при неизвестных и столбца свободных членов:
~
~
~
.
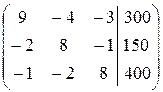
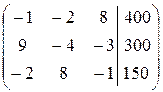
Используя полученную матрицу, выпишем преобразованную систему:
Прямой ход метода Гаусса закончен. Обратный ход заключается в том, что из последнего уравнения находят неизвестную 
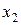, затем из второго – , а из первого – . Выполним это:
,
= 
,
= 
.
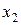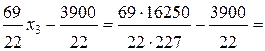
Итак, решение системы в неправильных дробях будет иметь вид: 
, 
, . Они будут выражать плановые объемы выпуска валовой продукции отраслей.
3. Выполним проверку полученного результата. Для этого подставим эти значения в исходную систему:
Вычисляя, получаем верные равенства.
4. Запишем приближенный ответ с точностью до сотых: 
; 
; 
.
Решение задания типа 11-20. Даны векторы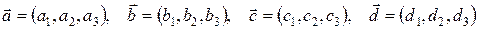 
в некотором базисе. Показать, что векторы 
образуют базис и найти координаты вектора 
в этом базисе. Систему линейных уравнений решить по формулам Крамера.
Например, 
Решение. Для того, чтобы векторы образовывали базис, необходимо показать, что векторы некомпланарны, т.е. их смешанное произведение 
отлично от нуля.
Вычислим смешанное произведение с помощью определителя третьего порядка:
= 
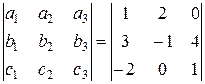= -23.
Поскольку = -23 
0, то векторы образуют базис в пространстве R 3.
Следовательно, любой вектор этого пространства единственным образом можно представить в ви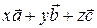де = 
, где 
- координаты вектора в базисе .
От векторного равенства перейдем к равенствам над соответствующими компонентами:
или 
Получили систему трех линейных уравнений с тремя неизвестными 
координаты вектора в новом базисе.
Решаем полученную систему методом Крамера, в соответствии с которым:
1) система трех линейных уравнений с тремя неизвестными имеет единственное решение, если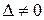 
- определитель третьего порядка, составленный из коэффициентов системы, не равен 0.
2) неизвестные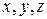 
находим по формулам Крамера
,
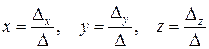где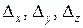 
- определители третьего порядка, составленные из определителя системы 
заменой коэффициентов, стоящих в системе перед 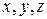, свободными членами соответственно:
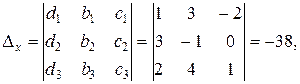
Тогда по формулам Крамера:
Проверка.
Получили тождества. Следовательно, система решена верно.
Ответ: 1) векторы 
образуют базис, 2) вектор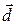 
в базисе 
имеет следующее разложение:
= 
.
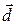