Найти область сходимости степенного ряда 
.
Решение. Данный ряд является обобщенным степенным рядом вида 
, где коэффициент 
, 
.
Областью сходимости степенного ряда с точностью до границ, является интервал с центром в точке 
и радиусом 
, где R – радиус сходимости степенного ряда определяется по формуле 
. Сходимость ряда на концах интервала при 
и 
необходимо исследовать отдельно. В нашем примере
, тогда 
.
Вычислим радиус сходимости = 
= 
= 
= 
= 
.
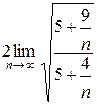Тогда интервал сходимости имеет вид 
или 
.
Исследуем сходимость степенного ряда на концах интервала. Пусть 
, тогда подставив это значение в степенной ряд, получим числовой ряд 
или, преобразовав его, имеем ряд 
. Мы получили числовой знакочередующийся ряд, который исследуется признаком Лейбница.
Согласно признаку Лейбница, если в знакочередующемся ряде выполняются два условия: 1) члены ряда с возрастанием номера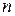 
, убывают по абсолютной величине; 2) предел абсолютной величины общего члена ряда равен нулю при 
, то такой ряд является сходящимся.
Проверим выполнимость условий Лейбница в нашем примере:
1) 
, 
, 
, 
, …, 
, 
, …
Очевидно, что члены ряда по абсолютной величине убывают:
> 
> 
> 
> …> 
> 
> …
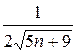2) 
.
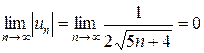Оба условия признака Лейбница выполняется, следовательно, при 
степенной ряд сходится.
Пусть , тогда данный степенной ряд станет числовым знакоположительным рядом 
=. 
.
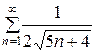К исследованию этого ряда на сходимость применим признак сравнения с рядом Дирихле 
, который сходится, если 
и расходится если 
.
Для нашего примера используем ряд 
= 
, здесь 
, значит, данный ряд расходится.
Сравнение выполним посредством вычисления предела 
= 
= 
= 
= 
= 
, так как предел получился отличным от 0 и 
, значит, исследуемый ряд 
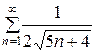ведет себя также, как и тот ряд, с которым проводилось сравнение , т.е. в нашем случае расходится, а это означает, что при степенной ряд 
расходится. Итак, область сходимости данного степенного ряда: 
.
Решение задания типа 151-160.
Производится залп из трех орудий. Вероятность попадания в цель первым орудием равна 0,9, вторым – 0,85, третьим – 0,95. Какова вероятность 1) хотя бы одного попадания в цель; 2) ровно двух попаданий.
Решение. Обозначим события 
. Из условия задачи вероятности этих событий равны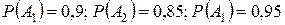 
. Соответственно, вероятности противоположных событий равны 
; 
; 
.
1) Требуется найти вероятность события 
. Противоположное событие 
.
Так как события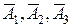 
независимы, то применима теорема умножения вероятностей: 
.
Известно, что 
. Отсюда 
.
2). Событие 
в алгебре событий с помощью событий 
можно записать как 
. Так как события 
и 
независимы и несовместны, то по теоремам сложения и умножения вероятностей получим 
= 
=
.