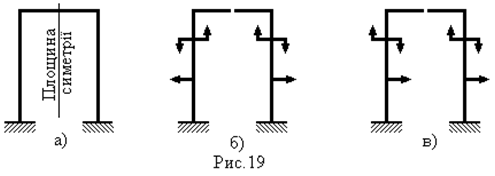
Якщо маємо деяку симетричну в геометричному відношенні раму (рис.19а), то її права частина може розглядатися як дзеркальне відображення лівої частини відносно плоскості симетрії.
|
При розрахунку таких рам можливо спростити рішення задачі і знизити число розшукуваних силових факторів 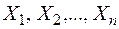 .
.
Розглянемо випадки, коли на раму діють симетричне чи кососиметричне навантаження. Під симетричним навантаженням будемо розуміти таку, при якій всі зовнішні сили, прикладені до правої частини рами, є дзеркальним відображенням сил, прикладених до лівої частини (рис. 19б). Під кососиметричним, або антисиметричним навантаженням будемо розуміти таку, при якій сили прикладені до правої половини рами, також є дзеркальним відображенням сил, прикладених до лівої половини, але протилежні їм за знаком (рис. 19в).
Відповідно класифікуємо і внутрішні силові фактори. Розглянемо для цього деякий довільний переріз рами, в якому діє шість силових факторів. В правій і лівій площинах довільного перерізу (рис. 20) сили і моменти рівні.
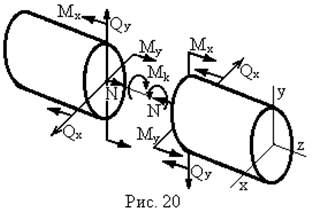
| Подивимось, які з шести силових факторів є дзеркальним відображенням відносно площини симетрії. Такими є три: два згинальних моменти 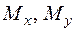 і поздовжня сила і поздовжня сила  . .
|
Будемо їх звати симетричними внутрішніми силовими факторами.
Крутний момент  і обидві поперечні сили
і обидві поперечні сили 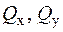 повинні бути названі кососиметричними силовими факторами. Кожний з них протилежний по знаку дзеркальному відображенню взаємного фактора. Неважко тепер довести наступні положення.
повинні бути названі кососиметричними силовими факторами. Кожний з них протилежний по знаку дзеркальному відображенню взаємного фактора. Неважко тепер довести наступні положення.
В симетричній рамі в площині симетрії при симетричному зовнішньому навантаженні нульовими будуть кососиметричні силові фактори, а при кососиметричному зовнішньому навантаженні – симетричні силові фактори.
Побічні питомі переміщення в системі (2.10) будуть рівними нулю при перемноженні епюр від симетричних силових факторів на епюри від кососиметричних силових факторів.
Це відбувається тому, що в симетричній рамі немає взаємних кососиметричних переміщень під дією симетричних навантажень. Таким же чином не буває симетричних переміщень від дії кососиметричних факторів. В результаті система канонічних рівнянь методу сил розпадається на дві незалежні системи.
Крім того, при симетричному зовнішньому навантаженні кососиметричні силові фактори в площині симетрії будуть дорівнювати нулю. При кососиметричному навантаженні нульовими будуть симетричні силові фактори в площині симетрії.
|
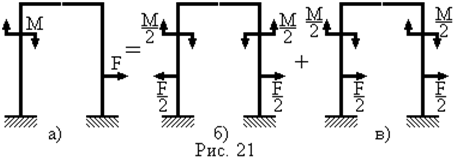
Якщо навантаження, прикладене до симетричної рами, не є ні симетричним, ні кососиметричним (рис. 21а), завжди мається можливість розкласти його на симетричне (рис. 21б) і кососиметричне (рис. 21в). Задача при цьому розпадається на дві. Розглядається окремо симетрична рама з кососиметричним навантаженням і рама з симетричним навантаженням. Внутрішні силові фактори в рамі далі визначаються накладенням знайдених рішень.
У випадку, коли рама має косу геометричну симетрію, можна шляхом сопоставлення епюр для двох половин рами спростити систему канонічних рівнянь.
Все наведене вище, зберігає силу не тільки для плоских, але і для просторових рам з будь-яким ступенем статичної невизначуваності.






