Обчислення інтегралів Мора істотно спрощується, якщо одна з епюр прямолінійна. Ця умова виконується для систем, що складаються з прямих стержнів, оскільки при цьому епюри внутрішніх сил від одиничного навантаження (зосередженої сили або пари) завжди обмежені прямими лініями.
Обчислимо інтеграл 
для випадку, коли 
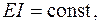епюра від заданого навантаження має довільну форму, а від одиничного – прямолінійна (рис. 2).
| Позначимо через  площу епюри  , С – її центр ваги,  – ординату епюри від одиничного навантаження під центром ваги епюри . Очевидно, що  є диференціалом площі епюри , а  . Тоді шуканий інтеграл
 (1.6)
|
Інтеграл у правій частині рівняння є статичним моментом площі епюри відносно осі О-О:
де 
– абсциса центра ваги епюри .
Тоді 
, оскільки 
.
Отже, інтеграл Мора дорівнює добутку площі епюри від зовнішнього навантаження на ординату одиничної епюри , розташованої під центром ваги епюри від заданого зовнішнього навантаження. Загальна формула (1.3) для визначення переміщень у системах з прямих стержнів набирає вигляду:
(1.7)
Графоаналітичний спосіб визначення інтеграла Мора був запропонований О.М.Верещагіним і має назву способу Верещагіна. Обчислення за цією формулою виконують по ділянках, на кожній з яких епюра від одиничного навантаження повинна бути прямолінійною. Тоді, коли обидві епюри прямолінійні, можна множити площу будь-якої з них на ординату іншої під центром ваги першої.
Якщо епюра має складний вигляд, то її слід розбити на прості фігури, для яких легко визначити площу і положення центра ваги. При цьому кожну з площ треба множити на ординату одиничної епюри під центром ваги відповідної площі. Ординати в цьому разі зручно позначати замість 
літерами 
, де 
.
Отже,
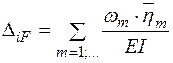(1.8)
Користуючись способом Верещагіна, необхідно пам'ятати, що добуток епюр позитивний, якщо ординати обох епюр відкладені з одного боку від осі стержня рами, і негативний, якщо ординати епюр відкладені з різних сторін. В тих випадках, коли одна з епюр криволінійна, береться площа 
криволінійної епюри, а ордината 
під центром ваги з прямолінійної епюри. При цьому треба враховувати правило знаків: Якщо епюри, що перемножуються, лежать по одну сторону (обидві нагорі або внизу), добуток позитивний; якщо епюри, що перемножуються, лежать по різні сторони - добуток негативний. Якщо одна або обидві епюри перетинають в межах дільниці нульову ось, то слідує перемножувати епюри по частинам. Особливості застосування правила Верещагіна видно з рис. 3а,б.
| 
|
| 
|
Рис. 3
Переміщення від дії осьових і поперечних сил, а також крутних моментів виражаються аналогічно:
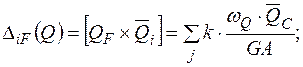(1.9)
де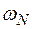 
- площа епюри 
, 
- площа епюри 
, 
- площа епюри 
від заданого навантаження; 
- ординати відповідних епюр осьових, поперечних сил і крутних моментів від одиничного навантаження, взяті під центрами ваги епюр , , .
Зазначимо, що епюри внутрішніх силових факторів від зовнішнього та одиничного навантажень на окремих ділянках стержня складаються з досить простих фігур: прямокутник, трикутник, парабола і т.д. Тоді для використання способу Верещагіна (1.8), (1.9) необхідно визначити площу та координату центра ваги цих простих фігур:
Таблиця 1
| Трикутник | Трикутник |
| 
|
| Прямокутник | Парабола (квадратна) з вершиною в т. А |
| 
|
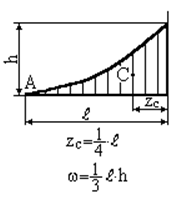
| Парабола (квадратна) з вершиною в т.А | Парабола (кубічна) з вершиною в т.А |
| 
|
Продовження таблиці 1
| Парабола (квадратна) з вершиною в т.А | Парабола (кубічна) з вершиною в т.А |
| 
|
