По медецинской информатике

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО

ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«БАШКИРСКИЙ ГОСУДАРСТВЕННЫЙ МЕДИЦИНСКИЙ УНИВЕРСИТЕТ»

ФЕДЕРАЛЬНОГО АГЕНСТВА ПО ЗДРАВООХРАНЕНИЮ И СОЦИАЛЬНОМУ

РАЗВИТИЮ РФ

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

И КОНТРОЛЬНЫЕ ЗАДАНИЯ

ПО МЕДЕЦИНСКОЙ ИНФОРМАТИКЕ

 

Учебное пособие для студентов стоматологических

факультетов медицинских ВУЗов

 

 

Уфа, 2012

 

 

УДК 61 (07 01)

Методические указания и контрольные задания по медицинской информатике. Учебное пособие для студентов стоматологических факультетов медицинских ВУЗов / Составители: Хайбуллина И.Р., Загитов Г.Н., Зелеев М.Х.; Уфа Башгосмедуниверситет. 2012. - 101 с.

Излагаются основные принципы работы с программными продуктами Microsoft Word и Microsoft Eхсе1, приводится обзор методов подготовки ком­плексных медицинских документов и обработки медицинской информации с использованием вычислительной техники и соответствующих программных продуктов Рассмотрены основы статистического анализа данных, разобраны правила анализа при решении конкретных задач.

Методические указания выполнены в соответствии с рабочей программой курса «Медицинская информатика» для студентов медицинских ВУЗов. утвер­жденной Департаментом образовательных медицинских учреждений и кадро­вой политики (2000 г); действующего учебною плана (2000 г); учебно- методического пособия «вопросы преподавания медицинской и биологической фишки, математики и информатики в медицинских ВУзах» под редакцией Ремизова А.Н. (1996 г.) и с учетом требований государственного стандарта Выс­шего профессионального образования по специальности «Сестринское дело» (2000 г).

Предназначены для студентов стоматологического факультета медицин­ских ВУЗов

 

Рецензенты; д.х.н., профессор,

Профессор кафедры

биохимии БГМУ

д.мед.н., Галимов Ш.Н.

 

Рекомендовано в печать Координационным научно-методически советом и утверждено решением редакционно-издательского совета Башгосмедуниверситета.

 

 

С Башкирский государственный медицинский университет.

С Методический кабинет. 2012

 

1. Тема: Решение задач математической статистики в Excel.

Актуальность. В результате наблюдений или эксперимента получаются наборы данных. С помощью математической статистики проводят их анализ. Важным разделом статистического анализа является корреляционный анализ, служащий для выявления взаимосвязей между выборками. При исследовании взаимосвязей между выборками используют регрессию. Электронная таблица Excel дает возможность обрабатывать результаты наблюдений, решать математические задачи. Формулы и функции составляют основу табличного процессора Microsoft Excel.

2. Учебные цели:

- получение навыков работы по созданию и редактированию таблиц;

- освоение приемов работы с мастером функций.

В результате освоения темы студент должен уметь:

- создавать и редактировать таблицы;

- использовать мастер функций для решения математических и статистических задач;

Для формирования умений студент должен знать:

- математические методы обработки результатов наблюдений (корреляционный и регрессионный анализ, дисперсионный анализ);

- приемы работы в электронной таблице Excel.

3. Материалы для самоподготовки к освоению данной темы.

Вопросы для самоподготовки:

1) Определение коэффициента корреляции.

2) Метод наименьших квадратов.

3) Составление выборочного уравнения линейной регрессии с помощью метода наименьших квадратов.

4) Возможности мастера функций пакета Excel и приемы работы с электронной таблицей.

4. Вид занятия: практическое занятие.

5. Продолжительность занятия: 3 академических часа.

6. Оснащение: компьютер с установленным пакетом MS Office.

7. Содержание занятия.

7.1. Контроль исходного уровня знаний.

Вопросы:

1. Функциональные возможности пакета Excel.

2. Ввод данных в пакете Excel.

3. Типы данных в электронной таблице.

4. Ввод формул в Excel.

5. Понятие коэффициента корреляции.

6. Составление выборочного уравнения линейной регрессии.

7. Формулы фактической и остаточной дисперсий.

8. Критерий Фишера-Снедекора.

7.2. Решение задач математической статистики в Excel.

Выборочный метод.

Раздел математики, посвященный методам сбора, анализа и обработки статистических данных, называется математической статистикой.

Совокупность всех единиц наблюдения, охватываемых таким сплошным наблюдением, называется генеральной совокупностью.

Множество объектов, случайно выбранных для исследования из всей генеральной совокупности, называется выборкой. Число объектов выборки называют ее объемом.

Пусть из генеральной совокупности извлечена выборка, причем x₁ наблюдалось n₁ раз, x₂ – n₂ раз, x_{k –} n_k раз и Sn_i=n – объем выборки. Наблюдаемые значения x_i называют вариантами, а последовательность вариант, записанных в возрастающем порядке, - вариационным рядом. Числа наблюдений называют частотами, а их отношения к объему выборки n_i/n – относительными частотами.

Статистическим распределением выборки называют перечень вариант и соответствующих им частот или относительных частот.

Над случайной величиной X проводится ряд независимых опытов и составляется статистическое распределение выборки количественного признака X. Чтобы получить представление о распределении случайной величины X, строят эмпирическую функцию распределения.

Эмпирической (выборочной) функцией распределения называют функцию F^*(x), определяющую для каждого значения x относительную частоту события X<x.

Для построения эмпирической функции распределения весь диапазон изменения случайной величины X разбивают на ряд интервалов одинаковой ширины. Затем определяют число значений случайной величины X, попавших в каждый интервал. Поделив эти числа на общее количество наблюдений n, находят относительную частоту попадания случайной величины X в заданные интервалы. По найденным относительным частотам строят гистограммы выборочных функций распределения. Если соответствующие точки относительных частот соединить ломаной линией, то полученная диаграмма будет называться полигоном частот.

Полигоном частот называют ломаную, отрезки которой соединяют точки (x₁;n₁), (x₂;n₂),…,(x_k;n_k).Для построения полигона частот на оси абсцисс откладывают варианты x_i, а на оси ординат – соответствующие им частоты n_i. Точки (x_i;n_i) соединяют отрезками прямых и получают полигон частот. Если откладывать на оси ординат относительные частоты, то получим полигон относительных частот.

Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиною Dx, а высоты равны отношению n_i/Dx (плотность частоты). Если высоты равны отношению относительной частоты на длину частичного интервала Dx, то гистограмму называют гистограммой относительных частот.

При увеличении до бесконечности размера выборки выборочные функции распределения превращаются в теоретические: гистограмма превращается в график плотности распределения, а кривая – в график функции распределения.

В Excel для построения эмпирических функций распределения используется специальная функция ЧАСТОТА и процедура пакета анализа Гистограмма.

Функция ЧАСТОТА вычисляет частоты появления случайной величины в интервалах значений и выводит их как массив цифр.

Процедура Гистограмма используется для вычисления выборочных и интегральных частот попадания данных в указанные интервалы значений. Процедура выводит результаты в виде таблицы и гистограммы.

Пример. Построить эмпирическое распределение следующей выборки: 24, 27, 23, 22, 25, 24, 27, 21, 20, 29, 23, 21, 26, 25,23, 22, 25, 26,23, 29.

Решение.

1. В ячейку А1 введите слово Наблюдения, а в диапазон А2:В11 – значения выборки.

2. Выберите ширину интервала 1. Тогда при крайних значениях 20 и 29 получится 9 интервалов. В ячейки С1 введите букву Х. В диапазон С2:С10 введите граничные значения интервалов (20, 21, 22, 23, 24, 25, 26, 27, 29).

3. Введите заголовки: в ячейку D1 – Абсолютные частоты, в ячейку E1 – Относительные частоты, в ячейку F1 – Накопленные частоты.

4. Заполните столбец абсолютных частот. Выделите ячейки D2:D10. Вызовите Мастер функций (кнопка f_x), категорию Статистические и функцию ЧАСТОТА, нажмите кнопку ОК. Появится диалоговое окно ЧАСТОТА.

 

Указателем мыши введите диапазон данных (А2:В11) в рабочее поле Массив данных. В рабочее поле Двоичный массив введите диапазон интервалов (С2:С10).

После этого нажмите комбинацию клавиш Ctrl+Shift+Enter. В столбце D2:D10 появится массив абсолютных частот.

5. Найдите объем выборки в ячейке D11. Для этого нажмите кнопку Автосумма, затем выберите диапазон суммирования (D2:D10) и нажмите клавишу Enter.

6. Заполните столбец относительных частот. Введите формулу в ячейку E2 для вычисления относительной частоты: =D2/D$11. Нажмите клавишу Enter. Протягиванием скопируйте формулу в диапазон E3:E10. Получим относительные частоты.

7. Заполните столбец накопленных частот. Относительную частоту, указанную в ячейке E2, наберите в ячейке F2. Введите формулу в ячейку F3:= F2+E3. Нажмите клавишу Enter. Протягиванием скопируйте формулу в диапазон: F4:F10. Получим накопленные частоты.

8. Результаты вычислений относительных частот и накопленных частот приводятся на рисунке.

 

	A	B	C	D	E	F
	Наблюдения	Х	Абсолютные частоты	Относительные частоты	Накопленные частоты
					0,05	0,05
					0,1	0,15
					0,1	0,25
					0,2	0,45
					0,1	0,55
					0,15	0,7
					0,1	0,8
					0,1	0,9
					0,1

 

9. Построим диаграмму относительных и накопленных частот. Щелкните указателем мыши по кнопке Мастер диаграмм. Выберите вкладку Нестандартные и тип диаграммы График/гистограмма 2. Затем нажмите кнопку Далее и укажите диапазон данных: E2:F10. Проверьте положение переключателя Ряды в: столбцах. Выберите вкладку Ряд и введите в рабочее поле Подписи оси X диапазон значений X C2:C10. Нажав кнопку Далее, введите названия осей X и Y: в рабочее поле Ось X - X; Ось Y - Относительная частота; Вторая ось Y - Накопленная частота. Нажмите кнопку Готово. Диаграмма будет иметь следующий вид:

 

 

Корреляционный анализ.

 

Одна из наиболее распространенных задач статистического исследования состоит в изучении связи между некоторыми наблюдаемыми переменными. Знание взаимозависимостей дает возможность предвидеть развитие ситуации при изменении характеристик объекта исследования.

Корреляционный анализ состоит в определении степени связи между двумя случайными величинами X и Y. В качестве меры такой связи используется коэффициент корреляции. Коэффициент корреляции двух независимых случайных величин равен нулю. Коэффициент корреляции двух величин, связанных линейной функциональной зависимостью, равен 1 в случае возрастающей зависимости и –1 в случае убывающей.

Выборочный коэффициент линейной корреляции между двумя случайными величинами X и Y рассчитывается по формуле

где x, y – значения признаков X и Y; n_xy – частота пары значений (x,y); n – объем выборки; s_x, s_y – выборочные средние квадратические отклонения; - выборочные средние.

, , , , ,

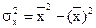После вычисления выборочного коэффициента корреляции проверим гипотезу о наличии существенности линейной корреляционной зависимости между изучаемыми величинами в генеральной совокупности, или, гипотезу о значимости выборочного коэффициента корреляции. Для этого вычисляем экспериментальное значение критерия:

t_эксп.= .

По таблице критических значений распределения Стьюдента при заданном уровне значимости a и числе степеней свободы f=n-2 находят критическое значение t_кр..

Если , то делают вывод о значимости выборочного коэффициента корреляции при приинятом уровне значимости.

В пакете Excel для вычисления коэффициента линейной корреляции используется специальная функция КОРРЕЛ. Параметрами функции являются КОРРЕЛ (массив 1; массив 2), где массив 1 – это диапазон ячеек первой случайной величины; массив 2 – это второй интервал ячеек со значениями второй случайной величины.

Пример. Изучали зависимость между систолическим давлением (мм рт. ст.) у мужчин в начальной стадии шока и возрастом X (годы).

Результаты наблюдений приведены в таблице.

X

 

Необходимо определить имеется ли взаимосвязь между систолическим давлением и возрастом.

Решение. Создайте рабочую таблицу в Excel. Введите в ячейку А1 слово “Возраст”. Затем в ячейки А1:А12 – соответствующие значения возраста. В ячейку В1 введите “Систолическое давление”. В ячейки В1:В12 – значения систолического давления. Затем вычисляется значение коэффициента корреляции между выборками. Установите курсор в свободную ячейку (А13). Нажмите кнопку Вставка функции (f_x) на панели инструментов. Выберите в диалоговом окне Мастер функций статистические функции, затем выберите функцию КОРРЕЛ.

Появится диалоговое окно КОРРЕЛ. Указателем мыши введите диапазон данных “Возраст” в поле массив 1 (А2:А12). Диапазон данных “Систолическое давление” введите в поле массив 2 (В2:В12).

В ячейке А13 после нажатия кнопки ОК появится значение коэффициента корреляции – 0,61. Если проверить значимость коэффициента корреляции между переменными X и при уровне значимости a=0,05 (при n=20 t_кр.=2,1), то можно сделать вывод, что имеется заметная линейная корреляционная связь между и X.

 

Регрессионный анализ.

 

Регрессионный анализ устанавливает формы зависимости между случайной величиной Y (зависимой) и значениями одной или нескольких переменных величин (независимых), причем значения последних считаются точно заданными. Такая зависимость обычно определяется некоторой математической моделью (уравнением регрессии), содержащей несколько неизвестных параметров.

Приведем уравнения регрессии Y на X и X на Y:

M(Y)_x=f(x), M(X)_y=j(y),

M(Y)_x – условное математическое ожидание величины Y, соответствующее значению x;

M(X)_y – условное математическое ожидание величины X, соответствующее значению y.

В результате n независимых опытов получены n пар чисел (x₁, y₁), (x₂, y₂), …, (x_n, y_n).

Найдем по данным наблюдений выборочное уравнение прямой линии регрессии.

Выборочное уравнение линейной регрессии Y на X будем искать в виде

(*)

Угловой коэффициент прямой линии регрессии Y на X называют выборочным коэффициентом регрессии Y на X.

Подберем параметры r_yx и b так, чтобы сумма квадратов отклонений ординат всех эмпирических точек от ординат соответствующих точек прямой (*) должна быть минимальной (в этом состоит сущность метода наименьших квадратов).

В результате применения метода наименьших квадратов получим следующие формулы для вычисления r_yx и b:

;

,

где , ,

, ,

,

.

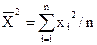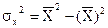Линейный регрессионный анализ заключается в подборе графика и его уравнения для набора наблюдений.

Для получения коэффициентов уравнения регрессии используется процедура Регрессия из пакета анализа. Кроме того, могут быть использованы функция ЛИНЕЙН для получения параметров регрессионного уравнения и функция ТЕНДЕНЦИЯ для получения предсказанных значений Y в требуемых точках.

Для реализации процедуры Регрессия необходимо:

- выполнить команду Сервис, Анализ данных;

- в появившемся диалоговом окне Анализ данных в списке Инструменты анализа выбрать строку Регрессия;

- в появившемся диалоговом окне задать Входной интервал Y. Для этого необходимо, нажав левую кнопку мыши, протянуть указатель мыши от верхней ячейки столбца зависимых данных к нижней ячейке, затем отпустить левую кнопку мыши;

- указать Входной интервал X. Для этого необходимо, нажав левую кнопку мыши, протянуть указатель мыши от верхней ячейки столбца независимых данных к нижней ячейке, затем отпустить левую кнопку мыши;

- указать выходной диапазон. Для этого следует навести указатель мыши в положение Выходной интервал и щелкнуть левой кнопкой, навести указатель мыши на правое поле ввода Выходной интервал и щелкнуть левой кнопкой мыши, затем указатель мыши навести на левую верхнюю ячейку выходного диапазона и щелкнуть левой кнопкой мыши. Размер выходного диапазона будет определен автоматически;

- если необходимо проверить отличие экспериментальных точек от предсказанных по регрессионной модели, следует установить флажок в поле График подбора;

- нажать кнопку ОК.

Результаты анализа. Выходной диапазон будет включать в себя результаты дисперсионного анализа, коэффициенты регрессии, стандартную погрешность вычисления Y, среднеквадратичные отклонения, число наблюдений, стандартные погрешности для коэффициентов.

Приводимое значение R – квадрат (коэффициент детерминации) в регрессионной статистике определяет, с какой степенью точности полученное регрессионное уравнение аппроксимирует исходные данные. Если R – квадрат > 0,95, говорят о высокой точности аппроксимации. Если R – квадрат лежит в диапазоне от 0,8 до 0,95, говорят об удовлетворительной аппроксимации. Если R – квадрат < 0,6, то точность аппроксимации недостаточна и модель требует улучшения.

В таблице Дисперсионный анализ оценивается общее качество полученной модели: ее достоверность по уровню значимости критерия Фишера – p, который должен быть меньше, чем 0,05. Значение p определяем в строке Регрессия, в столбце Значимость F.

Значения коэффициентов модели определяются из таблицы в столбце коэффициенты – в строке Y – пересечение приводится свободный член; в строках соответствующих переменных приводятся значения коэффициентов при этих переменных. В столбце p – значение приводится достоверность отличия соответствующих коэффициентов от нуля. В случаях, когда p > 0,5, коэффициент может считаться нулевым. Это означает, что соответствующая независимая переменная практически не влияет на зависимую переменную и коэффициент может быть убран из уравнения.

Пример. Изучали зависимость между объемом Y (мкм³) и диаметром X (мкм) сухого эритроцита у млекопитающих. Результаты наблюдений приведены в таблице:

 

X	Y
7,6
8,9
5,5
9,2
3,5
4,8
7,3
7,4
6,8

Необходимо на основании этих данных построить регрессионное уравнение.

Решение.

1. В пункте меню Сервис выберите строку Анализ данных

и далее укажите курсором мыши на строку Регрессия.

2. В появившемся диалоговом окне задайте Входной интервал Y.

3. Укажите Входной интервал X.

4. Установите флажок в поле График подбора.

5. Укажите выходной диапазон. Для этого поставьте переключатель в положение Выходной интервал, затем наведите указатель мыши на правое поле ввода Выходной интервал и, щелкнув левой кнопкой мыши, указатель мыши наведите на левую верхнюю ячейку выходного диапазона (C1). Щелкните левой кнопкой мыши. Нажмите кнопку ОК.

Результаты анализа. В выходном диапазоне появятся следующие результаты и график подбора.

 

ВЫВОД ИТОГОВ
Регрессионная статистика
Множественный R	0,94943
R-квадрат	0,901418
Нормированный R-квадрат	0,887335
Стандартная ошибка	9,446213
Наблюдения
Дисперсионный анализ
	df	SS	MS	F	Значимость F
Регрессия		5711,383	5711,383	64,00676	9,11E-05
Остаток		624,6166	89,23094
Итого
	Коэффициенты	Стандартная ошибка	t-статистика	P-Значение	Нижние 95%	Верхние 95%	Нижние 95,0%	Верхние 95,0%
Y-пересечение	-32,4752	12,50339	-2,59731	0,035564	-62,041	-2,90936	-62,041	-2,90936
Переменная X 1	14,28322	1,785308	8,000422	9,11E-05	10,06164	18,5048	10,06164	18,5048
ВЫВОД ОСТАТКА
Наблюдение	Предсказанное Y	Остатки
	76,07731	10,92269
	94,6455	-13,6455
	46,08255	3,917447
	98,93047	13,06953
	17,51611	0,483886
	36,0843	0,915701
	71,79235	-0,79235
	73,22067	-4,22067
	64,65074	-10,6507

 

В таблице Дисперсионный анализ оценивается общее качество полученной модели: ее достоверность по уровню значимости критерия Фишера (строка Регрессия, столбец Значимость F, в примере 0,0000911, то есть p=0,0000911 и модель значима).

Приводимое значение R – квадрат (коэффициент детерминации) в регрессионной статистике определяет степень точности описания моделью процесса. В примере R – квадрат=0,9015. Так как R – квадрат < 0,95, не можем говорить о высокой точности аппроксимации.

Определим значения коэффициентов модели. На пересечении строки Y – пересечение и столбца Коэффициент приводится свободный член. В строке Переменная X1 приводится коэффициент при X1.

Поэтому выражение для определения объема сухого эритроцита у млекопитающих от диаметра будет иметь вид:

 

Однофакторный дисперсионный анализ.

 

Для сравнения нескольких средних пользуются дисперсионным анализом. На практике дисперсионный анализ применяют, чтобы установить, оказывает ли существенное влияние некоторый качественный фактор А, который имеет m уровней А_1, А₂ … А _m на изучаемую величину Х. Например, если требуется выяснить, какая доза рентгеновского излучения наиболее эффективно влияет на темп размножения бактерий, то фактор А – рентгеновское излучение, а его уровни – дозы излучений.

Основная идея дисперсионного анализа состоит в сравнении факторной дисперсии и остаточной дисперсии. В математической статистике доказывается, что факторная дисперсия характеризует влияние фактора А на величину Х, а остаточная – влияние случайных причин.

Рассмотрим случай, когда число испытаний на различных уровнях различно. Пусть произведено q₁ испытаний на уровне А₁, q₂ испытаний на уровне А₂, …, q _m испытаний – на уровне А_m.

Общую сумму квадратов отклонений наблюдаемых зачений от общей средней х находят по формуле:

 

S_общ = [P₁ + P₂ + …+ P_m] – (R₁ +R₂ +… + R_m)²/n,

где

P₁ = 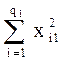- сумма квадратов наблюдавшихся значений признака на уровне А₁;

P₂ = 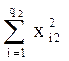- сумма квадратов наблюдавшихся значений признака на уровне А₂;

_...

 

P_m = 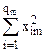- сумма квадратов наблюдавшихся значений признака на уровне А _m.

 

R₁ = , R₂ = 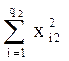… R_m = - суммы наблюдавшихся значений признака соответственно на уровнях А_1, А_{2, …} А_m.

 

n= q_{1 +} q_{2 +… +}q_m - общее число испытаний (объем выборки).

 

Факторную сумму квадратов отклонений групповых средних от общей средней, которая характеризует рассеяние " между группами" находят по формуле:

S_{факт =} [ (R₁²/q₁) + (R₂²/q₂ ) +… + (R_m²/q_m)] – [ (R₁ + R₂ + …+ R_m)² /n]

 

Остаточную сумму квадратов отклонений наблюдаемых значений группы от своей групповой средней, которая характеризует рассеяние "внутри групп", находят по формуле:

S _ост = S _общ -S _факт

Факторную дисперсию находят по формуле:

 

S² _факт = S _факт / (m-1)

Остаточную дисперсию находят по формуле:

S² _ост = S _ост /(n-m)

 

Сравниваем факторную и остаточную дисперсии.

Если факторная дисперсия окажется меньше остаточной, то фактор не оказывает существенное влияние на величину Х.

Если факторная дисперсия больше остаточной, то применяем критерий Фишера - Снедекора, для чего найдем наблюдаемое значение критерия

F _набл = S² _факт / S² _ост

 

По таблице “Критические точки распределения F Фишера - Снедекора” находим критическую точку F_кр (ά; m-1; n-m), ά – уровень значимости. Если F _набл > F_кр, то гипотезу о равенстве групповых средних отвергаем, значит фактор А оказывает существенное влияние на величину Х.

Для проведения в MS Excel дисперсионного анализа необходимо:

- ввести данные в таблицу. В каждом столбце должны быть данные, соответствующие одному значению исследуемого фактора. Столбцы должны располагаться в порядке возрастания (убывания) величины исследуемого фактора;

- выбрать команду Сервис, затем Анализ данных в списке Инструменты анализа выбрать процедуру Однофакторный дисперсионный анализ;

- в появившемся диалоговом окне задать Входной интервал, то есть таблицу данных;

- в разделе Группировка переключатель установить в положение по столбцам;

- указать выходной диапазон, то есть ввести ссылку на ячейки, в которые будут выведены результаты анализа.

 

Пример.

Определить достоверность влияния фермента (фактора А) на выход продукта биохимического синтеза при уровне значимости a£0,05.

№ испытания	Уровни фактора А А1 А2 А3 А4

Результаты анализа.

В результате будет получена таблица

Однофакторный дисперсионный анализ
ИТОГИ
Группы	Счет	Сумма	Среднее	Дисперсия
Столбец 1
Столбец 2			67,66667	4,333333
Столбец 3			71,33333	20,33333
Столбец 4			68,33333	2,333333
Дисперсионный анализ
Источник вариации	SS	df	MS	F	P-Значение	F критическое
Между группами	30,91667		10,30556	1,212418	0,366066	4,06618
Внутри групп			8,5
Итого	98,91667

В таблице Дисперсионный анализ на пересечении строки Между группами и столбца MS находится значение факторной дисперсии 10,30556. На пересечении строки Внутри групп и столбца MS находится значение остаточной дисперсии 8,5. Наблюдаемое значение критерия Фишера – Снедекора равно 1,212418. F критическое 4,06618. F_набл.<F_кр., следовательно фактор А не оказывает существенное влияние на величину X.

 

7.3. Самостоятельная работа студентов под контролем преподавателя.

1. С помощью Excel выполнить корреляционный анализ.

2. Выполнить регрессионный анализ, используя пакет Excel.

3. Выполнить дисперсионный анализ, используя электронную таблицу Excel.

7.4. Контроль освоения темы занятия.

Контрольные вопросы:

1. Понятие корреляционной зависимости.

2. Метод наименьших квадратов.

3. Формула для вычисления коэффициента корреляции.

4. Выборочное уравнение линейной регрессии.

5. Какие задачи можно решить с помощью дисперсионного анализа?

6. Формулы для вычисления факторной дисперсии и остаточной дисперсии.

7. Критерий Фишера – Снедекора.

8. Условия, необходимые при проведении дисперсионного анализа.

 

Тестовые задания.

 

1. Коэффициент корреляции двух независимых случайных величин равен

1. 0

2. 1

3. –1

4. 10

5. 0,5

2. Коэффициент корреляции двух величин, связанных линейной функциональной зависимостью, в случае возрастающей зависимости равен

1. 0

2. 1

3. –1

4. 10

5. 0,5

3. Коэффициент корреляции двух величин, связанных линейной функциональной зависимостью, в случае убывающей зависимости равен

1. 0

2. 1

3. –1

4. 10

5. 0,5

4. Корреляционная зависимость между величинами –

1. это когда изменение одной из величин влечет изменение математического ожидания другой.

2. это когда каждому значению одной величины поставлено в соответствие по некоторому правилу единственное значение другой величины.

5. Критерий оптимальности метода наименьших квадратов.

1. Сумма квадратов отклонений ординат всех эмпирических точек от ординат соответствующих точек прямой должна быть максимальной.

2. Сумма квадратов отклонений ординат всех эмпирических точек от ординат соответствующих точек прямой должна быть минимальной.

3. Сумма квадратов отклонений абцисс всех эмпирических точек от абцисс соответствующих точек прямой должна быть минимальной.

4. Сумма квадратов отклонений абцисс всех эмпирических точек от абцисс соответствующих точек прямой должна быть максимальной.

6. Коэффициент корреляции r=0. Это говорит о том, что:

1. Статистическая зависимость отсутствует.

2. Связь функциональная.

3. Корреляционная зависимость отсутствует.

4. Линейная корреляционная зависимость отсутствует.

7. О линейной регрессии говорят, если график регрессии изображается

1. Гиперболой.

2. Параболой.

3. Кривой.

4. Прямой.

8. Параметр “а” в уравнении регрессии характеризует:

1. Значение при х=0.

2. Свободный член.

3. Угловой коэффициент прямой.

9. Выборочный коэффициент корреляции является оценкой генерального коэффициента корреляции тем более точной, чем объем выборки:

1. Больше.

2. Меньше.

3. Не имеет значения.

4. Среди указанных ответов нет правильного.

10. Дисперсионный анализ применяют:

1. При изучении нормального закона распределения.

2. При описании форм зависимости между случайными переменными.

3. При изучении влияния факторов на результативный признак.

4. При установлении взаимосвязей между случайными величинами.

11. Для оценки достоверности действия фактора на результативный признак применяется критерий:

1. Стьюдента.

2. Пирсона.

3. Знаков.

4. Фишера.

12. Влияние фактора А на признак Х достоверно, если

1. S²_фак.<S²_ост.

2. S²_фак.>S²_ост.

3. F_эксп.<F_кр.(a,f₁,f₂)

4. F_эксп.>F_кр.(a,f₁,f₂)

13. Что называется дисперсионным анализом:

1. Статистический метод, позволяющий оценить влияние одного или нескольких факторов на результативный признак.

2. Раздел математики, посвященный методам систематизации, обработки и исследования статистических данных.

3. Статистический метод, определяющий правила проверки достоверности выводов анализа или правильности выдвигаемых гипотез.

4. Раздел математической статистики, занимающийся установлением взаимосвязей между случайными величинами.

14. Причина, вызывающая изменения величины результативного признака:

1. Объем выборки.

2. Точность измерения.

3. Контролируемые и неконтролируемые факторы.

4. Планирование эксперимента.

15. Достоинства дисперсионного анализа:

1. Позволяет определить действие каждого регулируемого фактора в отдельности.

2. Оценить действие различных сочетаний факторов на результативный признак.

3. Оценить достоверность коэффициента корреляции.

4. Сделать вывод о линейности влияния фактора на результативный признак.

 

 

Задания.

I. Построить эмпирическое распределение следующей выборки:

1. 23, 25,24,22,21,26,27,23,25,24,24,23,27,27,26,24,25,23,25,23.

2. 32,33,34,32,34,31,35,36,34,33,32,35,32,31,33,32,34,35,34,32.

3. 15,13,12,15,17,16,15,14,13,12,16,15,15,17,16,15,13,16,13,12.

4. 43,45,46,47,45,42,43,44,45,46,41,43,46,43,48,47,46,43,45,44.

5. 54,53,53,54,56,55,57,52,53,54,51,56,54,53,56,54,53,56,57,53.

6. 65,66,67,62,63,67,68,65,67,66,61,64,63,64,67,68,65,64,63,65.

7. 76,77,78,79,75,75,76,73,73,74,75,78,76,75,76,74,74,73,73,78.

8. 88,89,86,87,85,84,83,83,87,88,86,87,86,84,85,86,83,81,82,82.

9. 98,99,96,95,96,93,92,94,93,95,96,97,94,92,91,04,93,92,96,97.

10. 101,102,108,107,105,104,104,103,103,106,104,102,107,105,104,103,

103,106,105,107.

11. 53, 55,54,52,51,56,57,53,55,54,54,53,57,57,56,54,55,53,55,53.

12. 42,43,44,42,44,41,45,46,44,43,42,45,42,41,43,42,44,45,44,42.

13. 65,63,62,65,67,66,65,64,63,62,66,65,65,67,66,65,63,66,63,62.

14. 83,85,86,87,85,82,83,84,85,86,81,83,86,83,88,87,86,83,85,84.

15. 94,93,93,94,96,95,97,92,93,94,91,96,94,93,96,94,93,96,97,93.

16. 35,36,37,32,33,37,38,35,37,36,31,34,33,34,37,38,35,34,33,35.

17. 46,47,48,49,45,45,46,43,43,44,45,48,46,45,46,44,44,43,43,48.

18. 78,79,76,77,75,74,73,73,77,78,76,77,76,74,75,76,73,71,72,72.

19. 88,89,86,85,86,83,82,84,83,85,86,87,84,82,81,84,83,82,86,87.

20. 301,302,308,307,305,304,304,303,303,306,304,302,307,305,304,303,

303,306,305,307.

21. 43, 45,44,42,41,46,47,43,45,44,44,43,47,47,46,44,45,43,45,43.

22. 52,53,54,52,54,51,55,56,54,53,52,55,52,51,53,52,54,55,54,52.

23. 25,23,22,25,27,26,25,24,23,22,26,25,25,27,26,25,23,26,23,22.

24. 73,75,76,77,75,72,73,74,75,76,71,73,76,73,78,77,76,73,75,74.

25. 44,43,43,44,46,45,47,42,43,44,41,46,44,43,46,44,43,46,47,43.

26. 75,76,77,72,73,77,78,75,77,76,71,74,73,74,77,78,75,74,73,75.

27. 86,87,88,89,85,85,86,83,83,84,85,88,86,85,86,84,84,83,83,88.

28. 98,99,96,97,95,94,93,93,97,98,96,97,96,94,95,96,93,91,92,92.

29. 68,69,66,65,66,63,62,64,63,65,66,67,64,62,61,64,63,62,66,67.

30. 201,202,208,207,205,204,204,203,203,206,204,202,207,205,204,203,

203,206,205,207.

II. Даны результаты нескольких независимых наблюдений над системой случайных величин (x, y). Требуется найти выборочный коэффициент корреляции и проверить существенность корреляционной связи при уровне значимости a=0,05.

1. (2;3),(2,4;4),(3,4;5),(3,2;3),(4,3;5),(3,1;3),(3,3;5),(2,4;5),(4,2;1),(3,2;5)

2. (1;3),(2,3;6),(5,4;5),(4,2;3),(5,3;5),(4,1;3),(2,3;5),(6,4;5),(3,2;1),(4,2;5)

3. (5;3),(2,7;6),(6,4;5),(6,2;3),(7,3;5),(5,1;3),(4,3;5),(7,4;5),(6,2;1),(6,2;5)

4. (4;3),(7,7;6),(5,4;5),(8,2;3),(6,3;5),(7,1;3),(6,3;5),(5,4;5),(4,2;1),(7,2;5)

5. (4;3),(3,7;6),(7,4;4),(6,2;3),(5,3;5),(4,1;3),(7,3;5),(6,4;5),(5,2;1),(5,2;5)

6. (4;3),(3,7;6),(7,4;4),(6,2;3),(5,3;5),(4,1;3),(7,3;5),(6,4;5),(5,2;1),(5,2;5)

7. (5;3),(4,7;6),(6,4;4),(5,2;3),(4,3;5),(5,1;3),(4,3;5),(7,4;5),(6,2;1),(6,2;5)

8. (6;3),(7,7;6),(5,4;4),(4,2;3),(5,3;5),(5,1;3),(4,3;5),(7,4;5),(6,2;1),(6,2;5)

9. (5;3),(6,7;6),(4,3;4),(6,2;3),(6,3;5),(4,1;3),(3,3;5),(5,4;5),(4,2;1),(3,2;5)

10. (4;3),(6,7;6),(3,3;4),(5,2;3),(4,3;5),(5,1;3),(4,3;5),(6,4;5),(4,2;1),(6,2;5)

11. (3;3),(3,4;4),(2,4;5),(2,2;3),(3,3;5),(2,1;3),(4,3;5),(4,4;5),(2,2;1),(2,2;5)

12. (2;3),(5,3;6),(4,4;5),(3,2;3),(4,3;5),(3,1;3),(4,3;5),(5,4;5),(2,2;1),(4,2;5)

13. (4;3),(4,7;6),(5,4;5),(4,2;3),(6,3;5),(3,1;3),(4,3;5),(6,4;5),(3,2;1),(4,2;5)

14. (2;3),(6,7;6),(4,4;5),(3,2;3),(5,3;5),(2,1;3),(4,3;5),(4,4;5),(2,2;1),(5,2;5)

15. (2;3),(5,7;6),(5,4;4),(2,2;3),(4,3;5),(3,1;3),(6,3;5),(4,4;5),(2,2;1),(3,2;5)

16. (2;3),(5,7;6),(5,4;4),(2,2;3),(4,3;5),(3,1;3),(6,3;5),(4,4;5),(2,2;1),(4,2;5)

17. (4;3),(5,7;6),(5,4;4),(4,2;3),(5,3;5),(4,1;3),(5,3;5),(6,4;5),(2,2;1),(5,2;5)

18. (2;3),(5,7;6),(5,4;4),(3,2;3),(4,3;5),(3,1;3),(6,3;5),(5,4;5),(3,2;1),(4,2;5)

19. (4;3),(5,7;6),(3,3;4),(4,2;3),(5,3;5),(3,1;3),(4,3;5),(4,4;5),(2,2;1),(4,2;5)

20. (3;4),(5,7;6),(4,3;4),(4,2;3),(3,3;5),(4,1;3),(3,3;5),(5,4;5),(2,2;1),(5,2;5)

21. (4;3),(3,4;4),(4,4;5),(2,2;3),(3,3;5),(2,1;3),(4,3;5),(4,4;5),(2,2;1),(4,2;5)

22. (2;1),(5,3;6),(4,4;5),(3,2;3),(4,3;5),(3,1;3),(4,3;5),(5,4;5),(2,2;1),(6,2;5)

23. (4;3),(5,7;6),(4,4;5),(5,2;3),(6,3;5),(3,1;3),(4,3;5),(5,4;5),(2,2;1),(5,2;5)

24. (3;3),(6,7;6),(6,4;5),(3,2;3),(4,3;5),(3,1;3),(5,3;5),(4,4;5),(2,2;1),(6,2;5)

25. (2;3),(5,7;6),(5,4;4),(3,2;3),(4,3;5),(3,1;3),(5,3;5),(5,4;5),(4,2;1),(4,2;5)

26. (5;3),(5,7;6),(6,4;4),(3,2;3),(4,3;5),(3,1;3),(6,3;5),(5,4;5),(3,2;1),(4,2;5)

27. (4;5),(5,7;6),(5,4;4),(4,2;3),(5,3;5),(4,1;3),(3,3;5),(6,4;5),(3,2;1),(4,2;5)

28. (5;3),(6,7;6),(6,4;4),(3,2;3),(4,3;5),(4,1;3),(3,3;5),(4,4;5),(3,2;1),(4,2;5)

29. (6;4),(5,7;6),(5,3;4),(5,2;3),(4,3;5),(3,1;3),(4,3;5),(4,4;5),(3,2;1),(4,2;5)

30. (4;6),(5,4;6),(2,3;4),(3,2;3),(3,3;5),(4,1;3),(3,3;5),(4,4;5),(3,2;1),(4,2;5)

III. Даны результаты нескольких независимых наблюдений над системой случайных величин (x, y). Составить уравнение линейной регрессии Y на X.

1.(1;2),(3;4),(2;3),(2;6),(4;5),(4;3),(3;4),(3;5),(4;5),(4;6)

2.(1;5),(3;6),(4;3),(3;6),(6;5),(6;3),(7;4),(5;5),(3;5),(3;6)

3. (4;5),(6;6),(5;3),(6;7),(5;6),(7;3),(6;4),(4;5),(6;7),(3;7)

4.(5;6),(7;6),(4;3),(5;7),(7;6),(3;3),(5;4),(4;5),(6;5),(3;5)

5.(3;4),(1;2),(3;2),(2;3),(3;4),(3;5),(2;3),(3;4),(5;4),(3;6)

6.(3;1),(1;3),(1;2),(2;1),(2;5),(2;5),(1;3),(4;5),(2;5),(2;1)

7.(3;1),(2;3),(4;2),(3;1),(4;5),(3;5),(4;3),(2;5),(1;5),(4;1)

8. (4;1),(4;3),(5;2),(6;1),(3;5),(4;5),(4;3),(5;5),(4;5),(3;1)

9. (5;1),(3;3),(6;2),(5;1),(5;5),(3;5),(5;3),(3;5),(3;5),(4;1)

10. (4;1),(2;3),(7;2),(6;1),(5;5),(4;5),(3;3),(7;5),(6;5),(5;1)

11.(2;2),(2;4),(3;3),(5;6),(6;5),(3;3),(5;4),(6;5),(4;5),(5;6)

12.(2;5),(4;6),(3;3),(4;6),(4;5),(5;3),(6;4),(4;5),(3;5),(4;6)

13. (4;5),(5;6),(4;3),(5;7),(4;6),(6;3),(5;4),(3;5),(5;7),(4;7)

14.(4;6),(5;6),(5;3),(6;7),(5;6),(4;3),(6;4),(3;5),(6;5),(4;5)

15.(3;4),(3;2),(1;2),(4;3),(5;4),(4;5),(2;3),(5;4),(3;4),(3;6)

16.(3;2),(2;3),(3;2),(2;3),(3;5),(2;5),(2;3),(4;5),(3;5),(2;3)

17.(3;3),(4;3),(3;2),(3;1),(2;5),(3;5),(5;3),(3;5),(1;5),(4;3)

18. (4;3),(2;3),(4;2),(5;1),(3;4),(4;5),(2;3),(4;5),(3;5),(3;2)

19. (5;4),(3;4),(6;3),(5;4),(5;6),(3;4),(5;3),(4;5),(2;5),(4;2)

20. (4;2),(2;3),(4;2),(5;2),(5;4),(4;5),(2;3),(4;5),(6;5),(5;4)

21.(3;2),(3;4),(4;3),(5;6),(3;5),(4;3),(5;4),(3;5),(3;4),(4;4)

22.(4;5),(3;6),(4;5),(5;6),(4;5),(3;3),(6;4),(5;5),(4;5),(4;6)

23. (3;5),(5;6),(4;3),(6;5),(5;6),(6;3),(5;4),(4;5),(6;5),(3;4)

24.(5;4),(5;6),(4;3),(5;6),(5;6),(3;3),(5;4),(3;5),(4;5),(4;5)

25.(5;4),(3;2),(4;2),(2;3),(3;4),(4;5),(2;3),(3;5),(3;4),(3;6)

26.(3;2),(1;3),(3;2),(2;4),(2;3),(3;5),(2;3),(3;5),(2;4),(2;2)

27.(3;4),(2;3),(5;2),(4;1),(4;5),(5;5),(4;3),(3;5),(4;5),(4;1)

28. (4;3),(5;3),(5;2),(4;1),(2;5),(4;5),(2;3),(4;5),(3;5),(3;1)

29. (5;4),(3;3),(5;2),(5;3),(5;4),(3;5),(4;3),(3;5),(4;5),(4;2)

30. (4;3),(2;3),(6;2),(6;1),(5;5),(4;3),(5;3),(6;5),(6;5),(5;1)

VI. В предположении нормальности распределения величины X методом дисперсионного анализа при уровне значимости p=0,05 проверить значимость влияния фактора A на величину X по данным, приведенным в таблице:

1.

Номер испытания	Уровни фактора A   A1 A2 A3 A4

 

2.

Номер испытания	Уровни фактора A   A1 A2 A3 A4

 

3.

Номер испытания	Уровни фактора A   A1 A2 A3 A4

 

4.

Номер испытания	Уровни фактора A   A1 A2 A3 A4

 

5.

Номер испытания	Уровни фактора A   A1 A2 A3 A4

 

6.

Номер испытания	Уровни фактора A   A1 A2 A3 A4

 

7.

Номер испытания	Уровни фактора A   A1 A2 A3 A4

 

 

8.

Номер испытания	Уровни фактора A   A1 A2 A3 A4

 

9.

Номер испытания	Уровни фактора A   A1 A2 A3 A4

 

10.

Номер испытания	Уровни фактора A   A1 A2 A3 A4

 

11.

Номер испытания	Уровни фактора A   A1 A2 A3 A4

 

12.

Номер испытания	Уровни фактора A   A1 A2 A3 A4

 

13.

Номер испытания	Уровни фактора A   A1 A2 A3 A4

 

14.

Номер испытания	Уровни фактора A   A1 A2 A3 A4

---

12345678910Следующая ⇒

Поделиться с друзьями:

---

Дата добавления: 2015-11-05; Мы поможем в написании ваших работ!; просмотров: 799 | Нарушение авторских прав

---

Лучшие изречения:

© 2015-2024 lektsii.org - Контакты - Последнее добавление