Додаткові рівняння переміщень, що виражають рівність нулю переміщень (лінійних чи кутових) у напрямках зайвих невідомих, зручно складати в так званій канонічній формі, тобто за певною закономірністю.
| Спочатку розглянемо систему, один раз статично невизначувану (рис. 17а). Як зайву невідому виберемо шарнірно-рухому опору В. Тоді, навантаживши основну систему заданим навантаженням і зайвою невідомою силою  (рис.17б), прирівняємо до нуля повне переміщення точки В основної системи в напрямі :
|
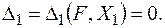(2.1)
Обчислюючи 
, застосуємо принцип незалежності дії сил: 
де 
– переміщення від заданого навантаження (рис. 17в);
– переміщення від сили .
Якщо 
– переміщення в напрямі від сили 
(рис.17г), то 
, і рівняння переміщень (2.1) набирає вигляду:
(2.2)
Це канонічна форма рівняння переміщень для один раз статично невизначуваної системи.
Для системи з двома зайвими зв’язками додаткові рівняння мають вигляд: 
де 
– повне переміщення в напрямі від заданого навантаження та зайвих невідомих сил і 
; 
– повне переміщення в напрямі від заданого навантаження та зайвих невідомих сил і .
Виходячи з принципу незалежності дії сил, запишемо переміщення та 
у вигляді сум переміщень, спричинених окремо кожною з невідомих сил , та заданим навантаженням 
. Використовуючи вибрані раніше позначення переміщень, знаходимо:
(2.3)
За аналогією можна записати в канонічній формі рівняння переміщень для будь-якої n разів статично невизначуваної системи:
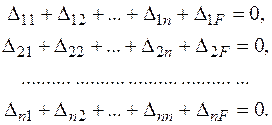(2.4)
Повне переміщення 
можна визначити як добуток питомого переміщення 
, спричиненого дією одиничної сили, на відповідну узагальнену силу – 
.
(2.5)
Система канонічних рівнянь методу сил для загального випадку навантаження має вигляд:
(2.6)
де 
– кількість зайвих зв'язків (ступінь статичної невизначуваності) системи.
Коефіцієнти 
рівнянь (2.6) являють собою лінійні зміщення та кути повороту в основній (статично визначуваній) системі від дії сил і моментів 
, доданих по напрямкам 
невідомих зусиль. Вільні члени 
визначають відповідні переміщення, викликані заданим зовнішнім навантаженням.
Коефіцієнти і вільні члени канонічних рівнянь (2.6) обчислюються за допомогою інтегралу Мора, що представляється в загальному випадку формулою[1].
(2.7)
де складання проводиться по усім дільницям пружної системи.
В прийнятій системі координат (вісь 
співпадає з віссю стержня, а 
і 
– головні центральні осі поперечного перерізу) крутний момент 
і згинальні моменти 
і 
, поздовжня 
та поперечні сили 
і 
є сукупністю проекцій головного вектору і головного моменту сил в довільному перерізі стержня.
При застосуванні графоаналітичних методів для визначення інтегралів Мора (2.7) необхідно мати відповідні епюри від одиничних навантажень 
, які будують для основної системи навантаженою тільки силами 
кожною окремо.
Епюри 
, будують також для основної системи, але від заданого зовнішнього навантаження. Ординати епюр згинальних моментів відкладають з боку стислого волокна.
Для багатопрольотної балки відмінними від нуля внутрішніми зусиллями вважати згинальний момент та поперечну силу.
Для плоскої рами - згинальний момент, поперечну і поздовжню сили.
Згідно з п.1.1, на підставі формули (2.7) знаходимо
(2.8)
Питомі переміщення, що мають однакові індекси й називаються головними коефіцієнтами канонічних рівнянь, визначають таким чином
(2.9)
Очевидно, що ці переміщення додатні.
Питомі переміщення, в яких індекси не однакові, називають побічними коефіцієнтами й визначають за формулою
(2.10)
Вони можуть бути додатними або від’ємними, а також дорівнювати нулю.
На підставі теореми про взаємність переміщень 
[1].
Плоскопросторові рами являють собою особливий клас стержньових конструкцій, у яких плоска рамна система навантажена силами, діючими в площинах, не співпадаючих з площиною самої рами 
.
|
Очевидно, що при дії сил, перпендикулярних площині рами (рис. 18), відмінними від нуля внутрішніми зусиллями в перерізі рами є
Якщо ж площина дії зовнішніх сил співпадає з площиною рами, відмінними від нуля є
Оскільки будь-яке зовнішнє навантаження можна розкласти на дві складові, одна з яких розміщена в площині рами 
, а інша – в перпендикулярній площині 
, ці невідомі поділяються на дві самостійні групи і можуть бути визначені незалежно друг від друга.
Таким чином, система канонічних рівнянь (2.6) для плоскопросторової рами в загальному випадку розпадається на дві незалежні системи:
(2.11)
Де 
– невідомі зусилля і моменти, діючі в площинах, ортогональних до площини рами;
– невідомі і моменти, що лежать в площині рами.
В випадку, якщо зовнішнє навантаження є антиплоским 
, 
, вільні члени 
системи (2.11) звертаються в нуль, що призводить до нульових рішень для зусиль в площині рами.
Отже, для плоскопросторових рам, навантажених ортогонально до її площини, ступінь статичної невизначуваності 
визначається числом додаткових зв'язків, накладених на раму в площині дії зовнішнього навантаження. Відмінними від нуля невідомими є зусилля, що призводять до появи згинальних і крутних моментів в площинах, перпендикулярних площині рами, причому нехтуємо впливом поздовжніх та поперечних сил:
(2.12)
Значення коефіцієнтів канонічних рівнянь, як показують вирази (2.7), залежать від співвідношення згинальних 
, 
та крутної 
жорсткостей поперечних перерізів стержньової системи та довжин 
відповідних ділянок стержня.
Якщо рама зібрана з прямолінійних стержнів постійної згинальної і крутної жорсткості, то безпосереднє інтегрування в формулі Мора можна замінити перемноженням епюр по способу Верещагіна (1.8).