МIНIСТЕРСТВО ОСВIТИ І НАУКИ УКРАЇНИ
НАЦІОНАЛЬНИЙ ТЕХНІЧНИЙ УНІВЕРСИТЕТ
“ХАРКIВСЬКИЙ ПОЛIТЕХНIЧНИЙ ІНСТИТУТ”
Конохов В.І.
Лавінський В.І.
Хавін В.Л.
РОЗРАХУНКИ СТАТИЧНО НЕВИЗНАЧУВАНИХ
СТЕРЖНЬОВИХ СИСТЕМ МЕТОДОМ СИЛ”
Навчально-методичний посібник
з розділу курсу “Опір матеріалів”
для студентів машинобудівних спеціальностей
ЗАТВЕРДЖЕНО
редакційно-видавничою
радою університету,
протокол №1
від 21.03.2002 р.
Харків НТУ “ХПІ” 2002
 |
ББК 30.121
К64
УДК 620.17
Р е ц е н з е н т и: д-р техн. наук, проф. О.К.Морачковський (Національний технічний університет “Харківський політехнічний інститут”),
канд-т техн. наук, проф. В.І.Пустинніков (Харківський державний технічний університет будівництва та архітектури)
Автори: Конохов В.І.
Лавінський В.І.
Хавін В.Л.
Розрахунки статично невизначуваних стержньових систем методом сил. Навчально - методичний посібник з розділу курсу “Опір матеріалів” для студентів машинобудівних спеціальностей. – Харків: НТУ “ХПІ”, 2002 –92с.
У першій главі посібника розглядаються методи визначення переміщень в пружних стержньових системах, наводяться приклади визначення переміщень для деяких простих розрахункових схем. У другій главі наведена методика розкриття статичної невизначуваності стержньових систем методом сил та приклади розв’язання статично невизначуваних задач. У третій главі посібника надаються розрахункові схеми і чисельні дані для виконання індивідуальних розрахунково-проектувальних завдань, а також приклади їх розв’язання та оформлення.
Посібник призначений для студентів машинобудівних спеціальностей. Може бути корисним для викладачів, а також для аспірантів та наукових працівників, які у своїй практичній діяльності стискаються з необхідністю розв’язання статично невизначуваних задач у стержньових системах.
Іл. 45. Табл. 5. Бібліогр. 2 назв. ББК 30.121
 |
Зміст
Вступ. 5
1 Енергетичні методи визначення переміщень в стержньових системах 7
1.1 Інтеграл Максвелла – Мора. 7
1.2 Обчислення інтегралів Мора способом перемноження епюр (способом Верещагіна). 10
1.3 Перемноження епюр за правилами трапецій і Сімпсона – Карнаухова. 15
1.4 Приклади визначення переміщень. 17
Приклад 1. 17
Приклад 2. 19
Приклад 3. 21
Приклад 4. 26
2 Статично невизначувані системи. 36
2.1 Основні поняття та визначення. 36
2.2 Метод сил. 39
2.3 Канонічні рівняння методу сил. 42
2.4 Використання властивостей симетрії при виборі основної статично визначуваної системи. 48
2.5 Перевірка правильності розрахунків. 50
2.6 Приклади розкриття статичної невизначуваності 52
Приклад 1. 52
Приклад 2. 56
Приклад 3. 59
3 Розрахунково – проектувальне завдання. 66
Задача 1. Визначення внутрішніх зусиль у статично невизначуваних балках. 71
Чисельні дані до задачі №1. 74
Задача 2. Визначення внутрішніх зусиль у статично невизначуваних рамах. 75
Чисельні дані до задачі №2. 79
Задача 3. Визначення внутрішніх зусиль в статично невизначуваних плоскопросторових рамах та визначення розмірів поперечного перерізу 80
Чисельні дані до задачі 3. 84
Типи перерізів до задачі 3. 85
Контрольна задача № 4. (Для самостійної роботи) 86
Контрольна задача № 5. (Для самостійної роботи) 89
Чисельні дані для контрольних задач №4, №5. 93
Зразок виконання розрахунку статично невизначуваної балки. 94
Зразок виконання розрахунку статично невизначуваної рами. 99
Зразок виконання розрахунку статично навизначуваної плоскопросторової рами. 103
Література. 107
Контрольні питання. 108
Вступ
Однією з найважливіших задач опору матеріалів є оцінка жорсткості конструкції, тобто ступеня її викривлення під дією силового навантаження, зміщення зв’язків, зміни температури.
Для розв’язання цієї задачі треба визначити переміщення (лінійні та кутові) довільно навантаженої пружної системи (балки, рами, криволінійного стержня, або ферми). Визначення переміщень є необхідною частиною розрахунків на жорсткість, а також складовою частиною метода сил при розкритті статичної невизначуваності стержньових систем, які є розрахунковими схемами різноманітних конструкцій. В останньому випадку складають рівняння спільності деформацій, які містять у собі переміщення певних точок системи. Визначення переміщень є основною задачею при розрахунку конструкцій на динамічні навантаження.
Загальний метод визначення переміщень у стержньових системах заснован на двох фундаментальних принципах механіки: початку можливих переміщень і законі зберігання енергії.
Як відомо з теоретичної механіки, робота постійної сили 
на переміщенні D за її напрямком дорівнює добутку значення сили на зазначене переміщення:
.
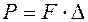У задачах опору матеріалів і будівельної механіки зовнішні навантаження відзначаються великою різноманітністю і, як правило, становлять групи сил. Вираз для роботи групи постійних сил також можна подати у вигляді добутку двох величин:
,
у якому множник залежить тільки від групи сил і називається узагальненою силою, а 
залежить від переміщень і називається узагальненим переміщенням.
Переміщення, яке спричинене одиничною силою 
або одиничною парою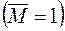 
, будемо позначати літерою 
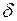і називати одиничним. При цьому умовимося вважати одиничні сили чи пари, які спричиняють переміщення 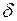, безрозмірними.
Якщо одинична сила 
спричинила переміщення 
, то, згідно з принципом незалежності дії сил, повне переміщення, яке викликано силою , дорівнює:
.
Отже, під узагальненою силою будемо розуміти будь-яке навантаження (зосереджені сили, зосереджені моменти, розподільне навантаження), а під узагальненим переміщенням – той вид переміщення, на якому узагальнена сила здійснює роботу.
Розглядаючи досить жорсткі лінійно деформовані конструкції (тобто системи, деформації яких малі і відповідають закону Гука), можна на підставі принципу незалежності дії сил визначати повні переміщення точок як суму переміщень, спричинених окремими навантаженнями.
Зазначимо, що навантаження, яке діє на конструкцію, як правило, позначають літерами 
з числовими індексами (наприклад, 
). У цьому разі літерні індекси при 
або 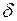замінюють відповідними числовими, тобто замість 
пишуть 
.
Енергетичні методи визначення переміщень в стержньових системах
Інтеграл Максвелла – Мора
Розглянемо довільну плоску стержньову систему (балку, раму, ферму), навантажену заданими зовнішніми силами (рис. 1а).
| Зусилля в довільному перерізі системи позначимо через  . Визначимо переміщення (узагальнене)  будь-якої точки системи в напрямі m-m. Введемо допоміжний стан (рис. 1б), що є заданою системою, навантаженою лише однією одиничною силою (узагальненою)  , прикладеною в тій самій точці і в напрямі шуканого переміщення . Зусилля в довільному перерізі допоміжного стану, спричинені дією одиничної сили , позначимо  .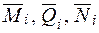
|
Застосуємо початок можливих переміщень для допоміжного стану, ввівши як можливі дійсні переміщення заданої системи [1]:
(1.1)
де 
– кількість ділянок розрахункової схеми, k – коефіцієнт форми перерізу.
Вираз (1.1) є загальною формулою для пружного переміщення плоскої стержньової системи.
Якщо виходити з виразу початку можливих переміщень [1], то у загальному випадку просторової стержньової системи при довільному навантаженні загальна формула для визначення пружного переміщення містить шість додатків і її можна записати і вигляді:
(1.2)
Індекси “x”, “y” в формулі (1.2) позначають головні осі перерізу ділянки стержня, індекс “к” – крутний момент. Зазначимо, що наведені формули можна застосовувати і для криволінійних стержнів малої кривизни.
Формули (1.1) та (1.2) вперше були виведені Максвеллом (для поздовжніх переміщень) і Мором. Визначення переміщень за цими формулами часто називають методом Максвелла – Мора. Зазначимо, що метод Максвелла – Мора – це найзагальніший метод визначення переміщень стержньових систем.
Здебільшого при визначенні переміщень у балках, рамах та криволінійних брусах можна знехтувати впливом поздовжніх деформацій і деформацій зсуву, враховуючи лише переміщення, спричинені згинанням і крученням. При цьому для балок та плоских рам впливом поперечних та поздовжніх сил, як правило, нехтують і враховують лише згинальні моменти 
. Однак, визначаючи переміщення в балках, для яких відношення висоти перерізу до довжини прольоту 
поперечні сили враховувати обов’язково. При визначенні переміщень в рамах з великими зазначеними відношеннями 
похибка, спричинена неврахуванням інтегралів поздовжніх та поперечних сил, також може стати істотною. Слід мати на увазі, що в реальних балочних та рамних конструкціях величина відношення 
, як правило, менше за 
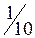. Тому при обчисленні переміщень у загальній формулі Максвелла – Мора цілком допустимо зберегти інтеграл, що враховує лише згинальні моменти [1].
Тоді формула (1.1) для плоскої системі набирає вигляду
, (1.3)
і називається інтегралом Мора.
При просторовому навантажуванні, згідно з формулою (1.2),
(1.4)
При визначенні переміщень вузлів шарнірних ферм, що складаються з прямих стержнів, які працюють лише на розтягання – стискання у формулі Мора зберігається тільки один додаток:
(1.5)
Ця формула має назву формули Максвелла.
Можна запропонувати таку послідовність визначення переміщень за допомогою інтеграла Максвелла – Мора:
Будують допоміжну систему, яку навантажують одиничним навантаженням у точці, де треба визначити переміщення і в напрямку, в якому треба визначити переміщення. Визначаючи лінійні переміщення, у заданому напрямі прикладають одиничну силу, визначаючи кутові переміщення, - одиничний момент.
Для кожної ділянки системи записують вирази силових факторів у довільному перерізі заданої 
і допоміжної 
систем.
Обчислюють інтеграли Максвелла - Мора (по ділянках в межах всієї системи). Як вже зазначалося, при розрахунку плоских балок, рам і арок виходять з формули (1.3), просторових систем – (1.4), ферм – (1.5).
Якщо обчислене переміщення позитивне, то це означає, що його напрям збувається з вибраним напрямом одиничної сили. Негативний знак свідчить про те, що дійсний напрям переміщення, що визначається, протилежний напряму одиничної сили.
