t-распределение (распределение Стьюдента)

P (t > t_a) = a и P (|t| > t_a) = a

Таблица 1

k	Односторонняя критическая область (a)
0,1	0,05	0,025	0,01	0,005	0,0025	0,001	0,0005
Двусторонняя критическая область (a)
0,2	0,1	0,05	0,02	0,01	0,005	0,002	0,001
¥	3,08 1,89 1,64 1,53 1,48 1,44 1,41 1,40 1,38 1,37 1,36 1,36 1,35 1,34 1,34 1,34 1,33 1,33 1,33 1,33 1,32 1,32 1,32 1,32 1,32 1,32 1,31 1,31 1,31 1,31 1,30 1,30 1,29 1,28	6,31 2,92 2,35 2,13 2,02 1,94 1,89 1,86 1,83 1,81 1,80 1,78 1,77 1,76 1,75 1,75 1,74 1,73 1,73 1,72 1,72 1,72 1,71 1,71 1,71 1,71 1,70 1,70 1,70 1,70 1,68 1,67 1,66 1,64	12,71 4,30 3,18 2,78 2,57 2,45 2,36 2,31 2,26 2,23 2,20 2,18 2,16 2,14 2,13 2,12 2,11 2,10 2,09 2,09 2,8 2,07 2,07 2,06 2,06 2,06 2,05 2,05 2,05 2,04 2,02 2,00 1,98 1,96	31,82 6,96 4,54 3,75 3,36 3,14 3,00 2,90 2,82 2,76 2,72 2,68 2,65 2,62 2,60 2,58 2,57 2,55 2,54 2,53 2,52 2,51 2,50 2,49 2,49 2,48 2,47 2,47 2,46 2,46 2,42 2,39 2,36 2,33	63,66 9,92 5,84 4,60 4,03 3,71 3,50 3,36 3,25 3,17 3,11 3,05 3,01 2,98 2,95 2,92 2,90 2,88 2,86 2,85 2,83 2,82 2,81 2,80 2,79 2,78 2,77 2,76 2,76 2,75 2,70 2,66 2,62 2,58	127,32 14,09 7,45 5,60 4,77 4,32 4,03 3,83 3,69 3,58 3,50 3,43 3,37 3,33 3,29 3,25 3,22 3,20 3,17 3,15 3,14 3,12 3,10 3,09 3,08 3,07 3,06 3,05 3,04 3,03 2,97 2,91 2,85 2,81	318,30 22,33 10,21 7,17 5,89 5,21 4,79 4,50 4,30 4,14 4,02 3,93 3,85 3,79 3,73 3,69 3,65 3,61 3,58 3,55 3,53 3,51 3,48 3,47 3,45 3,44 3,42 3,41 3,40 3,39 3,31 3,23 3,16 3,09	636,61 31,60 12,92 8,61 6,87 5,96 5,41 5,04 4,78 4,59 4,44 4,32 4,22 4,14 4,07 4,02 3,97 3,92 3,88 3,85 3,82 3,79 3,77 3,75 3,73 3,71 3,69 3,67 3,66 3,65 3,55 3,46 3,37 3,29

Таблица значений функции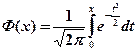

Таблица 2

x
0,0	0,00000
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9

1,0
1,1
1,2
1,3
1,4
1,5
1,6
1,7
1,8
1,9

2,0
2,1
2,2
2,3
2,4
2,5
2,6
2,7
2,8
2,9

3,0	0,49865	0,49865	3,1		3,2		3,3		3,4
3,5			3,6		3,7		3,8		3,9
4,0			-	-	-	-	-	-	-	-

Критические значения выборочного коэффициента корреляции r_a

Таблица 3

Уровни значимости, a
n	0,05	0,01	0,001	n	0,05	0,01	0,001
	0,9969	0,999877	0,99999877		0,388	0,496	0,607
	0,950	0,9900	0,9990		0,381	0,487	0,597
	0,878	0,9597	0,99114		0,374	0,479	0,588
	0,811	0,9172	0,9741		0,367	0,470	0,579
	0,754	0,875	0,9509		0,361	0,463	0,570
	0,707	0,834	0,9244		0,349	0,449	0,554
	0,666	0,798	0,898		0,332	0,435	0,539
	0,632	0,765	0,872		0,325	0,418	0,519
	0,602	0,735	0,847		0,312	0,402	0,501
	0,576	0,708	0,823		0,304	0,393	0,490
	0,553	0,684	0,801		0,292	0,384	0,416
	0,532	0,661	0,780	'47	0,288	0,372	0,465
	0,544	0,641	0,760		0,279	0,361	0,451
	0,497	0,623	0,742		0,273	0,354	0,443
	0,482	0,606	0,725		0,254	0,330	0,414
	0,468	0,590	0,708		0,220	0,286	0,380
	0,456	0,575	0,693		0,196	0,258	0,324
	0,444	0,561	0,679		0,175	0,230	0,286
	0,433	0,549	0,665		0,160	0,210	0,249
	0,423	0,537	0,652		0,124	0,163	0,207
	0,413	0,526	0,641		0.088	0,115	0,147
	0,404	0,515	0,629		0,062	0,081	0,104
	0,396	0,505	0,618

Критерий Колмогорова – Смирнова

Точные и асимптотические границы для верхней грани модуля разности

Истинной и эмпирической функции распределения

Таблица 4

n	Уровень значимости 0,05	Уровень значимости 0,01
	точная граница	асимптотическая граница	отношение	точная граница	асимптотическая граница	отношение
	0,5633 0,4087 0,3375 0,2939 0,2639 0,2417 0,2101 0,1884 0,1723 0,1597 0,1496 0,1412 0,1340	0,6074 0,4295 0,3507 0,3037 0,2716 0,2480 0,2147 0,1921 0,1753 0,1623 0,1518 0,1432 0,1358	1,078 1,051 1,039 1,033 1,029 1,026 1,022 1,019 1,018 1,016 1,015 1,014 1,013	0,6685 0,4864 0,4042 0,3524 0,3165 0,2898 0,2521 0,2260 0,2067 0,1917 0,1795	0,7279 0,5147 0,4202 0,3639 0,3255 0,2972 0,2574 0,2302 0,2101 0,1945 0,1820	1,089 1,058 1,040 1,033 1,028 1,025 1,021 1,018 1,016 1,015 1,014

При n > 100 следует принять асимптотические границы

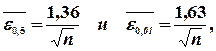
для которых истинные коэффициенты доверия несколько больше заданных величин 0,95 и 0,99 соответственно.

Распределение Пирсона (х² – распределение)

Значения х²_таблдля вероятностей Р (х² > х²_табл)

Таблица 5

n	Вероятность
0,999	0,995	0,99	0,98	0,975	0,95	0,90	0,80	0,75	0,70	0,50
	0,05157 0,00200 0,0243 0,0908 0,210 0,381 0,598 0,857 1,152 1,479 1,834 2,214 2,617 3,041 3,483 3,942 4,416 4,905 5,407 5,921 6,447 6,983 7,529 8,035 8,649 9,222 9,803 10,391 10,986 11,588	0,04393 0,0100 0,0717 0,207 0,412 0,676 0,989 1,344 1,735 2,156 2,603 3,074 3,565 4,075 4,601 5,142 5,697 6,265 6,844 7,434 8,034 8,643 9,260 9,886 10,520 11,160 11,808 12,461 13,121 13,787	0,03157 0,0201 0,115 0,297 0,554 0,872 1,239 1,646 2,088 2,558 3,053 3,571 4,107 4,660 5,229 5,812 6,408 7,015 7,633 8,260 8,897 9,542 10,196 10,856 11,524 12,198 12,879 13,565 14,256 14,953	0,03628 0,0404 0,185 0,429 0,752 1,134 1,564 2,032 2,532 3,059 3,609 4,178 4,765 5,368 5,985 6,614 7,255 7,906 8,567 9,237 9,915 10,600 11,293 11,992 12,697 13,409 14,125 14,847 15,574 16,306	0,03982 0,0506 0,216 0,484 0,831 1,237 1,690 2,180 2,700 3,247 3,816 4,404 5,009 5,629 6,262 6,908 7,564 8,231 8,907 9,591 10,283 10,982 11,688 12,401 13,120 13,844 14,573 15,308 16,047 16,791	0,0093 0,103 0,352 0,711 1,145 1,635 2,167 2,733 3,325 3,240 4,575 5,226 5,892 6,571 7,261 7,962 8,672 9,390 10,117 10,871 11,591 12,338 13,091 13,848 14,611 15,379 16,151 16,928 17,708 18,493	0,0158 0,211 0,584 1,064 1,610 2,204 2,833 3,490 4,168 4,865 5,578 6,304 7,042 7,790 8,547 9,312 10,085 10,865 11,651 12,443 13,240 14,041 14,848 15,659 16,173 17,292 18,114 18,937 19,768 20,599	0,0642 0,446 1,005 1,649 2,343 3,070 3,822 4,594 5,380 6,179 6,989 7,807 8,634 9,467 10,307 11,152 12,002 12,857 13,716 14,578 15,445 16,314 17,187 18,062 18,940 19,830 20,703 21,588 22,475 23,364	0,102 0,575 1,213 1,923 2,675 3,455 4,255 5,071 5,899 6,787 7,584 8,438 9,299 10,165 11,036 11,912 12,892 13,675 14,562 15,452 16,344 17,240 18,137 19,037 19,939 20,843 21,749 22,657 23,567 24,478	0,148 0,713 1,424 2,195 3,000 3,828 4,671 5,527 6,393 7,267 8,148 9,034 9,926 10,821 11,721 12,624 13,531 14,440 15,352 16,266 17,182 18,101 19,021 19,943 20,887 21,792 22,719 23,617 24,577 25,508	0,455 1,386 2,366 3,357 4,351 5,348 6,346 7,344 8,343 9,342 10,341 11,340 12,340 13,339 14,339 15,338 16,338 17,338 18,338 19,337 20,337 21,337 22,337 23,337 24,337 25,336 26,136 27,386 28,336 29,336

Таблица 6

n	Вероятность
0,30	0,25	0,20	0,10	0,05	0,025	0,02	0,01	0,005	0,001
	1,074 2,408 3,665 4,878 6,064 7,231 8,383 9,524 10,656 11,781 12,899 14,011 15,119 16,222 17,322 18,418 19,511 20,601 21,689 22,775 23,858 24,939 26,018 27,096 28,172 29,246 30,319 31,391 32,461 33,530	1,323 2,773 4,108 5,385 6,626 7,841 9,037 10,219 11,389 12,549 13,701 14,845 15,984 17,117 18,245 19,369 20,489 21,605 22,718 23,828 24,935 26,039 27,141 28,241 29,339 30,434 31,528 32,620 33,711 34,800	1,642 3,219 4,642 5,989 7,289 8,558 9,803 11,030 12,242 13,412 14,631 15,812 16,985 18,151 19,311 20,465 21,615 22,760 23,900 25,038 26,171 28,429 29,553 30,675 31,795 32,912 34,027 35,139 36,250	2,706 4,605 6,251 7,779 9,236 10,645 12,017 13,362 14,684 15,987 17,275 18,549 19,812 21,064 22,307 23,542 24,769 25,989 27,204 28,412 29,615 30,813 32,007 33,196 34,328 35,563 36,741 37,916 39,087 40,256	3,841 5,991 7,815 9,488 11,070 12,592 14,067 15,507 16,919 18,307 19,675 21,026 22,362 23,685 24,996 26,296 27,587 28,869 30,144 31,410 32,671 33,924 35,172 36,415 37,652 38,885 40,113 41,337 42,557 43,773	5,024 7,378 9,348 11,143 12,839 14,449 16,013 17,535 19,023 20,483 21,920 23,337 24,736 26,119 27,488 28,845 30,191 31,526 32,852 34,170 35,479 36,781 38,076 39,364 40,046 41,923 43,194 44,461 45,722 46,979	5,412 7,824 9,837 11,668 13,388 15,033 16,622 18,168 19,679 21,161 22,618 24,054 25,472 26,873 28,259 29,633 30,995 32,346 33,687 35,020 36,343 37,659 38,968 40,270 41,566 42,856 44,140 45,419 46,693 47,962	6,635 9,210 11,345 13,277 15,086 16,812 18,475 20,090 21,666 23,209 24,725 26,217 27,688 29,141 30,578 32,000 33,409 34,805 36,191 37,566 38,932 40,289 41,638 42,980 44,314 45,642 46,963 48,278 49,588 50,892	7,879 10,597 12,838 14,860 16,750 18,548 20,278 21,955 23,589 25,188 26,757 28,300 29,819 31,319 32,801 34,267 35,718 37,156 38,582 39,997 41,401 42,796 44,181 45,558 46,928 48,290 49,645 50,993 52,336 53,672	10,827 13,815 16,268 18,465 20,517 22,457 24,322 26,125 27,877 29,588 31,264 32,909 34,528 36,123 37,697 39,252 40,790 42,312 43,820 45,315 46,797 48,268 49,728 51,170 52,620 54,052 55,476 56,893 58,302 59,703

Распределение Фишера – Снедекора (F-распределение)

Значения F_табл, удовлетворяющие условию P(F > F_табл). Первое значение соответствует вероятности 0,05; второе – вероятности 0,01 и третье – вероятности 0,001; n₁ – число степеней свободы числителя; n₂ – знаменателя

Таблица 7

n₁ n₂										¥	t
	161,4 18,51 98,49 998,46 10,13 34,12 67,47 7,71 21,20 74,13 6,61 16,26 47,04 5,99 13,74 35,51 5,59 12,25 29,22 5,32 11,26 25,42 5,12 10,56 22,86 4,96 10,04 21,04	199,5 19,00 99,01 999,00 9,55 30,81 148,51 6,94 18,00 61,24 5,79 13,27 36,61 5,14 10,92 26,99 4,47 9,55 21,69 4,46 8,65 18,49 4,26 8,02 16,39 4,10 7,56 14,91	215,7 19,16 99,17 999,20 9,28 29,46 141,10 6,59 16,69 56,18 5,41 12,06 33,20 4,76 9,78 23,70 4,35 8,45 18,77 4,07 7,59 15,83 3,86 6,99 13,90 3,71 6,55 12,55	224,6 19,25 99,25 999,20 9,12 28,71 137,10 6,39 15,98 5,19 11,39 31,09 4,53 9,15 21,90 4,12 7,85 17,19 3,84 7,10 14,39 3,63 6,42 12,56 3,48 5,99 11,28	230,2 19,30 99,30 999,20 9,01 28,24 134,60 6,26 15,52 51,71 5,05 10,97 20,75 4,39 8,75 20,81 3,97 7,46 16,21 3,69 6,63 13,49 3,48 6,06 11,71 3,33 5,64 10,48	234,0 19,33 99,33 999,20 8,94 27,91 132,90 6,16 15,21 50,52 4,95 10,67 28,83 4,28 8,47 20,03 3,87 7,19 15,52 3,58 6,37 12,86 3,37 5,80 11,13 3,22 5,39 9,92	238,9 19,37 99,36 999,40 8,84 27,49 130,60 6,04 14,80 49,00 4,82 10,27 27,64 4,15 8,10 19,03 3,73 6,84 14,63 3,44 6,03 12,04 3,23 5,47 10,37 3,07 5,06 9,20	243,9 19,41 99,42 999,60 8,74 27,05 128,30 5,91 14,37 47,41 4,68 9,89 26,42 4,00 7,72 17,99 3,57 6,47 13,71 3,28 5,67 11,19 3,07 5,11 9,57 2,91 4,71 8,45	249,0 19,45 99,46 999,40 8,64 26,60 125,90 5,77 13,93 45,77 4,53 9,47 25,14 3,84 7,31 16,89 3,41 6,07 12,73 3,12 5,28 10,30 2,90 4,73 8,72 2,74 4,33 7,64	253,3 19,50 99,50 999,40 8,53 26,12 123,50 5,63 13,46 44,05 4,36 9,02 23,78 3,67 6,88 15,75 3,23 5,65 11,70 2,99 4,86 9,35 2,71 4,31 7,81 2,54 3,91 6,77	12,71 63,66 636,2 4,30 9,92 31,00 3,18 5,84 12,94 2,78 4,60 8,61 2,57 4,03 6,86 2,45 3,71 5,96 2,36 3,50 5,40 2,31 3,36 5,04 2,26 3,25 4,78 2,23 3,17 4,59

Продолжение таблицы 7

n₁ n₂										¥	t
	4,84 9,65 19,69 4,75 9,33 18,64 4,67 9,07 17,81 4,60 8,86 17,14 4,45 8,68 16,59 4,41 8,53 16,12 4,45 8,40 15,72 4,41 8,28 15,38 4,38 8,18 15,08 4,35 8,10 14,82 4,32 8,02 14,62 4,30 7,94 14,38	3,98 7,20 13,81 3,88 6,93 12,98 3,80 6,70 12,31 3,74 6,51 11,78 3,68 6,36 11,34 3,63 6,23 10,97 3,59 6,11 10,66 3,55 6,01 10,39 3,52 5,93 10,16 3,49 5,85 9,95 3,47 5,78 9,77 3,44 5,72 9,61	3,59 6,22 11,56 3,49 5,95 10,81 3,41 5,74 10,21 3,34 5,56 9,73 3,29 5,42 9,34 3,24 5,29 9,01 3,20 5,18 8,73 3,16 5,09 8,49 3,13 5,01 8,28 3,10 4,94 8,10 3,07 4,87 7,94 3,05 4,82 7,80	3,36 5,67 10,35 3,26 5,41 9,63 3,18 5,20 9,07 3,11 5,03 8,62 3,06 4,89 8,25 3,01 4,77 7,94 2,96 4,67 7,68 2,93 4,58 7,46 2,90 4,50 7,26 2,87 4,43 7,10 2,84 4,37 6,95 2,82 4,31 6,87	3,20 5,32 9,58 3,11 5,06 8,89 3,02 4,86 8,35 2,96 4,69 7,92 2,90 4,56 7,57 2,85 4,44 7,27 2,81 4,34 7,02 2,77 4,25 6,81 2,74 4,17 6,61 2,71 4,10 6,46 2,68 4,04 6,32 2,66 3,99 6,19	3,09 5,07 9,05 3,00 4,82 8,38 2,92 4,62 7,86 2,85 4,46 7,44 2,79 4,32 7,09 2,74 4,20 6,80 2,70 4,10 6,56 2,66 4,01 6,35 2,63 3,94 6,18 2,60 3,87 6,02 2,57 3,81 5,88 2,55 3,75 5,76	2,95 4,47 8,35 2,85 4,50 7,71 2,77 4,30 7,21 2,70 4,14 6,80 2,64 4,00 6,47 2,59 3,89 6,20 2,55 3,79 5,96 2,51 3,71 5,76 2,48 3,63 5,59 2,45 3,56 5,44 2,42 3,51 5,31 2,40 3,45 5,19	2,79 4,40 7,62 2,69 4,16 7,00 2,60 3,96 6,52 2,53 3,80 6,13 2,48 3,67 5,81 2,42 3,55 5,55 2,38 3,45 5,32 2,34 3,37 5,13 2,31 3,30 4,97 2,28 3,23 4,82 2,25 3,17 4,70 2,23 3,12 4,58	2,61 4,02 6,85 2,50 3,78 6,25 2,42 3,59 5,78 2,35 3,43 5,41 2,29 3,29 5,10 2,24 3,18 4,85 2,19 3,08 4,63 2,15 3,01 4,45 2,11 2,92 4,29 2,08 2,86 4,15 2,05 2,80 4,03 2,03 2,75 3,92	2,40 3,60 6,00 2,30 3,36 5,42 2,21 3,16 4,97 2,13 3,00 4,60 2,07 2,87 4,31 2,01 2,75 4,06 1,96 2,65 3,85 1,92 2,57 3,67 1,88 2,49 3,52 1,84 2,42 3,38 1,82 2,36 3,26 1,78 2,30 3,15	2,20 3,11 4,49 2,18 3,06 4,32 2,16 3,01 4,12 2,14 2,98 4,14 2,13 2,95 4,07 2,12 2,92 4,02 2,11 2,90 3,96 2,10 2,88 3,92 2,09 2,86 3,88 2,09 2,84 3,85 2,08 2,83 3,82 2,07 2,82 3,79

Продолжение таблицы 7

n₁ n₂										¥	t
¥	4,28 7,88 14,19 4,26 7,82 14,03 4,24 7,77 13,88 4,22 7,72 13,74 4,21 7,68 13,61 4,19 7,64 13,50 4,18 7,60 13,39 4,17 7,56 13,29 4,00 7,08 11,97 3,84 6,64 10,83	3,42 5,66 9,46 3,40 5,61 9,34 3,38 5,57 9,22 3,37 5,53 9,12 3,35 5,49 9,02 3,34 5,45 8,93 3,33 5,42 8,85 3,32 5,39 8,77 3,15 4,98 7,76 2,99 4,60 6,91	3,03 4,76 7,67 3,01 4,72 7,55 2,99 4,68 7,45 2,98 4,64 7,36 2,96 4,60 7,27 2,95 4,57 7,18 2,93 4,54 7,12 2,92 4,51 7,05 2,76 4,13 6,17 2,60 3,78 5,42	2,80 4,26 6,70 2,78 4,22 6,59 2,76 4,18 6,49 2,74 4,14 6,41 2,73 4,11 6,33 2,71 4,07 6,25 2,70 4,04 6,19 2,69 4,02 6,12 2,52 3,65 5,31 2,37 3,32 4,62	2,46 3,94 6,08 2,62 3,90 5,98 2,60 3,86 5,89 2,59 3,82 5,80 2,57 3,78 5,73 2,56 3,75 5,66 2,54 3,73 5,59 2,53 3,70 5,53 2,37 3,34 4,76 2,21 3,02 4,10	2,53 3,71 5,56 2,51 3,67 5,55 2,49 3,63 5,46 2,47 3,59 5,38 2,46 3,56 5,31 2,44 3,53 5,24 2,43 3,50 5,18 2,42 3,47 5,12 2,25 3,12 4,37 2,09 2,80 3,74	2,38 3,41 5,09 2,36 3,36 4,99 2,34 3,32 4,91 2,32 3,29 4,83 2,30 3,26 4,76 2,29 3,23 4,69 2,28 3,20 4,65 2,27 3,17 4,58 2,10 2,82 3,87 1,94 2,51 3,27	2,20 3,07 4,48 2,18 3,03 4,39 2,16 2,99 4,31 2,15 2,96 4,24 2,13 2,93 4,17 2,12 2,90 4,11 2,10 2,87 4,05 2,09 2,84 4,00 1,92 2,50 3,31 1,75 2,18 2,74	2,00 2,70 3,82 1,98 2,66 3,84 1,96 2,62 3,66 1,95 2,58 3,59 1,93 2,55 3,52 1,91 2,52 3,46 1,90 2,49 3,41 1,89 2,47 3,36 1,70 2,12 2,76 1,52 1,79 2,13	1,76 2,26 3,05 1,73 2,21 2,97 1,71 2,17 2,89 1,69 2,13 2,82 1,67 2,10 2,76 1,65 2,06 2,70 1,64 2,03 2,64 1,62 2,01 2,59 1,39 1,60 1,90 1,03 1,04 1,05	2,07 2,81 3,77 2,06 2,80 3,75 2,06 2,79 3,72 2,06 2,78 3,71 2,05 2,77 3,69 2,05 2,76 3,67 2,05 2,76 3,66 2,04 2,75 3,64 2,00 2,66 3,36 1,96 2,58 3,29

Библиографический список

1. Баврин И.И. Высшая математика: учеб. для студ. высш. учеб. заведений /И.И. Баврин, В.Л. Матросов. – М.: Владос, 2002. –400с.

2. Берман Г.Н. Сборник задач по курсу математического анализа: учеб. пособие для втузов / Г.Н. Берман.– СПб.: Лань, Специальная литература, 2000. – 448с. – (Учебники для втузов. Специальная литература).

3. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике: учеб. пособие для студентов вузов / В.Е. Гмурман.– 9-е изд., стер. – М.: «Высшая школа», 2004. – 404 с.

4. Горелова Г.В. Теория вероятностей и математическая статистика в примерах и задачах с применением Excel: учеб. пособие для вузов / Г.В. Горелова, И.А. Кацко..– 3-е изд., доп. и перераб – Ростов н/Д.: ООО Феникс, 2005. – 480 с.

5. Горлач Б.А. Математика: учеб. пособие для вузов, обучающихся по экономическим специальностям /Б.А. Горлач. – М.: ЮНИТИ-ДАНА, 2006. – 911 с.

6. Данко П.Е. Высшая математика в упражнениях и задачах. В 2ч. Ч.2: учеб. пособие для втузов / П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова. – 6-е изд.– М.: ООО «Издательство дом» «ОНИКС 21 век»: ООО «Издательство «Мир и Образование», 2003. – 416 с.

7. Демидович Б.П. Краткий курс высшей математики: учеб. пособие для втузов / Б.П. Демидович, В.А. Кудрявцев.– М.: ООО «Издательство Астрель»: «Издательство АСТ», 2003. – 654с.

8. Математика: теория вероятностей и математическая статистика: учеб. пособие / М.П. Булаев [и др.] – Рязань: РГМУ, 2002.– 205 с.

9. Натансон И.П. Краткий курс высшей математики / И.П. Натансон. – 4-е изд., стереотипное. – СПб.: Лань, 2001. – 736 с. – (Учебники для вузов. Специальная литература).

Сборник задач по высшей математике / К.Н. Лунгу [и др.]. – М.: Рольф, 2001. – 576 с.

10. Фадеева Л.Н. Математика для экономистов: Теория вероятностей и математическая статистика. Задачи и упражнения / Л.Н. Фадеева, Ю.В. Жуков, А.В. Лебедев. – М.: Эксмо, 2006. – 336 с.

Содержание

Глава 1. Предел функции. 3

1.1. Определение предела. 3

1.2. Операции над пределами. 4

1.3. Замечательные пределы.. 5

1.4. Примеры.. 6

1.5. Варианты заданий. 8

1.6. Контрольные вопросы.. 10

Глава 2. Производная и дифференциал. 10

2.1 Понятие производной. 10

2.2. Геометрический и физический смысл производной. 10

2.3. Таблица производных. 12

2.4. Основные правила дифференцирования. 12

2.5. Производные высших порядков. 13

2.6. Дифференциал функции. 13

2.7. Геометрический смысл и свойства дифференциала. 14

2.8. Дифференциалы высших порядков. 15

2.9. Примеры.. 15

2.10. Варианты заданий. 17

Глава 3. Исследование функций и построение графиков. 21

3.1. Промежутки монотонности и знакопостоянства. 21

3.2. Экстремумы функции. 21

3.3. Выпуклость и вогнутость функции. Точка перегиба. 23

3.4. Асимптоты.. 24

3.5.Общая схема исследования функции и построение графиков. 25

3.6. Примеры.. 25

3.7. Варианты заданий. 31

3.8. Контрольные вопросы.. 32

Глава 4. Функции нескольких переменных. 32

4.1. Определение функции нескольких переменных. 32

4.2. Частные производные. 33

4.3. Полный дифференциал. 34

4.5. Примеры.. 34

4.6. Варианты заданий. 36

4.7. Контрольные вопросы.. 36

Глава 5. Численное дифференцирование. 36

5.1. Формулы для вычисления первой производной. 37

5.2. Формулы второй производной. 38

5.3. Примеры.. 39

5.4. Варианты заданий. 42

Глава 6 Основы интерполяции. 43

6.1. Постановка задачи. 43

Интерполяционные формулы конечных разностей. 45

6.3. Интерполяционные формулы центральных разностей. 46

6.4. Интерполирование функции с не равноотстоящими узлами. 47

6.5. Варианты заданий. 53

6.6. Контрольные вопросы.. 54

Глава 7. Неопределенный интеграл. 54

7.1. Первообразная функция и неопределенный интеграл. 54

7.2. Основные свойства неопределенного интеграла. 55

7.3. Таблица простейших интегралов. 56

7.4. Основные методы интегрирования. 57

7.4.1. Непосредственное интегрирование. 57

7.4.2. Метод подстановки (замена переменной) 57

7.4.3. Интегрирование по частям.. 58

7.5. Примеры.. 59

7.6. Варианты заданий. 62

7.7. Контрольные вопросы.. 63

Глава 8. Определенный интеграл. 63

8.1. Основные понятия и свойства определенного интеграла. 64

8.2. Основные методы интегрирования. 66

8.2.1. Формула Ньютона-Лейбница. 66

8.2.2. Метод подстановки. 67

8.2.3. Интегрирование по частям.. 68

8.3. Примеры.. 68

8.4. Варианты заданий. 71

8.5. Биологические, физические и медицинские приложения определенного интеграла. 72

Глава 9. Численное интегрирование. 81

9.1. Формула прямоугольников. 81

9.2. Формула трапеций. 82

9.4. Формула Симпсона. 83

9.5. Примеры.. 84

9.6. Варианты заданий. 89

9.7. Контрольные вопросы.. 90

Глава 10. Дифференциальные уравнения. 91

10.1. Основные определения. 91

10.2. Уравнения с разделяющимися переменными. 93

10.3. Однородные уравнения первого порядка. 94

10.4. Линейные уравнения первого порядка. 94

9.5. Примеры.. 96

10.6. Варианты заданий. 103

10.7. Применение дифференциальных уравнений в биологии и медицине. 105

10.8. Варианты заданий. 109

10.9. Контрольные вопросы.. 111

Глава 11. Численные методы решения дифференциальных уравнений. 111

11.1. Метод Эйлера. 112

10.2. Метод Рунге – Кутта. 113

10.3. Примеры.. 114

11.4. Варианты заданий. 117

11.4. Контрольные вопросы.. 119

Глава 12. Элементы теории вероятностей. 119

12.1. Случайное событие. 119

12.2. Комбинаторика. 120

12.3. Вероятность случайного события. 122

Закон сложения вероятностей. 124

12.5. Варианты заданий. 125

12.6. Условная вероятность, закон умножения вероятностей. 129

12.7. Варианты заданий. 133

12.8. Формулы полной вероятности и Байеса. 136

12.9. Варианты заданий. 139

11.10. Формулы Бернулли, Пуассона и Муавра-Лапласа. 144

12.11. Варианты заданий. 151

12.2. Случайные величины.. 155

12.3. Варианты заданий. 164

Глава 13. Статистический анализ результатов исследований. 166

13.1. Основные понятия математической статистики. 166

13.1. Варианты заданий. 171

13.2. Статистические оценки параметров распределения. Выборочные характеристики 172

13.3. Варианты заданий. 175

13.4. Оценка параметров генеральной совокупности по ее выборке. 176

13.5. Варианты заданий. 179

13.6. Интервальная оценка параметров генеральной совокупности. 179

13.7. Варианты заданий. 185

1.8. Контрольные вопросы.. 186

Глава 14. Корреляционный и регрессионный анализ. 186

14.1. Функциональная и корреляционная зависимости. 187

14.2. Коэффициент линейной корреляции и его свойства. 189

14.3. Проверка гипотезы о значимости выборочного коэффициента линейной корреляции 192

14.4. Выборочное уравнение линейной регрессии. Метод наименьших квадратов. 194

14.5. Нелинейная регрессия. 199

14.6. Варианты заданий. 200

Приложение. 203

t-распределение (распределение Стьюдента) 203

Таблица значений функции 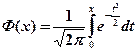................................. 205

Критические значения выборочного коэффициента корреляции r_a. 207

Критерий Колмогорова – Смирнова. 208

Точные и асимптотические границы для верхней грани модуля разности. 208

истинной и эмпирической функции распределения. 208

Распределение Пирсона (х² – распределение) 209

Распределение Фишера – Снедекора (F-распределение) 213

Библиографический список. 219