Это ответ на вопрос: существует ли вообще эта связь.
Эмпирический коэффициент корреляции, как и любой другой выборочный показатель, служит оценкой своего ге 
нерального параметра. Выборочный коэффициент линейной корреляции rв - величина случайная, так как он вычисляется по значениям переменных, случайно попавшим в выборку из генеральной совокупности, а значит, как и любая случайная величина, имеет ошибку тr.
Чтобы выяснить, находятся ли случайные величины X и Y генеральной совокупности в линейной корреляционной зависимости, надо проверить значимость rв. Для этого проверяют нулевую гипотезу о равенстве нулю коэффициента корреляции генеральной совокупности H 0: rген = 0, то есть линейная корреляционная связь между признаками X и Y случайна. Выдвигается альтернативная гипотеза H 1: rген ≠ 0, то есть эта линейная корреляционная связь имеется. Задается уровень значимости, например, α ≤ 0,05.
Критерием для проверки нулевой гипотезы является отношение выборочного коэффициента корреляции к своей ошибке:
где тr - ошибка коэффициента корреляции.
Если объем выборки п < 100, то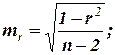 
;
если объем выборки п > 100, то 
.
Число степеней свободы для проверки критерия равно f = п - 2. Гипотезу проверяют по таблицам распределения Стьюдента в соответствии с выбранным уровнем значимости.
По таблице критических точек распределения Стьюдента находим tкрит (α, f), определенное на уровне значимости α ≤ 0,05 при числе степеней свободы f = п - 2, где n - объем двумерной выборки.
Если tнабл > tкрит => H 1- отвергают нулевую гипотезу и принимают альтернативную: rген ≠ 0, имеется линейная корреляционная связь между признаками.
Если tнабл < tкрит - то нет оснований отвергать нулевую гипотезу, а rв статистически незначим. Эта связь случайна.
Проверить значимость коэффициента корреляции r = 0,74 между переменными X и Y для выборки объема n = 50.
Решение:
Проверяется нулевая гипотеза H 0 об отсутствии линейной корреляционной связи между переменными X и Y в генеральной совокупности H 0: rген = 0.
При справедливости этой гипотезы 
, где ошибка коэффициента корреляции 
и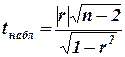 
имеют распределение Стьюдента сf = n- 2 степенями свободы.
Рассчитаем: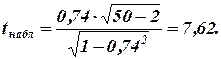 
.
По таблицам находим табличное значение t -критерия Стьюдента, определенное на уровне значимости α ≤ 0,05 и при числе степеней свободы f = 50 - 2 = 48, tкрит (α ≤ 0,05; 48) = 2,02.
Поскольку tнабл > tкрит, 7,62 > 2,02, коэффициент корреляции значимо отличается от нуля.
Причем это справедливо и для уровня значимости:
α ≤ 0,001 (t = 3,55).
По выборке объема п = 122, извлеченной из нормальной двумерной совокупности (X, Y), найден выборочный коэффициент линейной корреляции r = 0,4. При уровне значимости α ≤ 0,05 проверить нулевую гипотезу H 0, которая заключается в том, что связь между признаками случайна.
Решение:
Сравниваем: tнабл > tкрит (α, f), 5,24 > 1,98 => H 1 – отвергается нулевая гипотеза.
Вывод: имеется умеренная линейная корреляционная связь между признаками: r = 0,4 (α ≤ 0,05).
