Характеристики положения
Мода (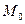
) – это такое значение варианты, что предшествующее и следующее за ним значения имеют меньшие частоты встречаемости или = 
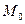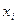, такое, что n(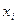) = max.
Для одномодальных распределений мода – это наиболее часто встречающаяся варианта в данной совокупности.
Например, для распределения:
|
| ||||
|
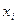
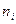
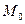=18= 
, так как 
=20=max.
Для определения моды интервальных рядов служит формула:
где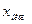 
- нижняя граница модального интервала, т. е. интервала с наибольшей частотой встречаемости 
; - частота модального интервала; 
- частота интервала, предшествующего модальному;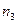 
- частота интервала, следующего за модальным; 
- ширина интервала.
Определить моду ряда распределения кальция (мг %) в сыворотке крови обезьян.
| Интервалы | 8,6-9,3 | 9,4-10,1 | 10,2-10,9 | 11,0-11,7 | 11,8-12,5 | 12,6-13,3 | 13,4-14,1 | 14,2-14,9 |
| Частота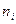
|
Решение: Частота модального класса = 25, его нижняя граница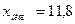 
. Частота класса, предшествующего модальному, = 23; частота класса, следующего за модальным, 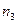= 17; = 0,8. Подставим эти данные в формулу, находим:
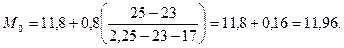
Найдите моду распределения роста 1000 взрослых мужчин:
| Рост, см | Число мужчин | Рост, см | Число мужчин |
| 143-145 | 167-169 | ||
| 146-148 | 170-172 | ||
| 149-151 | 173-175 | ||
| 152-154 | 176-178 | ||
| 155-157 | 179-181 | ||
| 158-160 | 182-184 | ||
| 161-163 | 185-187 | ||
| 164-166 |
Решение:
Медиана Ме – это значение признака, относительно которого ряд распределения делится на 2 равные по объему части.
Например, в распределении:
12 14 16 18 20 22 24 26 28
медианой будет центральная варианта, т.е. Ме = 20, так как по обе стороны от нее отстоит по 4 варианты.
Для ряда с четным числом членов 6 8 10 12 14 16 18 20 22 24 медианой будет полусумма его центральных членов, т.е.
Выборочная средняя – это среднее арифметическое значение вариант статистического ряда
есть оценка математического ожидания случайной величины по выборке.
В выборке взрослых мужчин n = 50 определяли содержание гемоглобина в крови. У =30 оно оказалось равным в среднем 70%. Для другой группы мужчин = 20 этот показатель составил 50%. Найти среднюю арифметическую из этих двух средних.
Решение:
По формуле: 
Характеристики рассеяния вариант вокруг своего среднего
Выборочная дисперсия – среднее арифметическое квадратов отклонения вариант от их среднего значения:
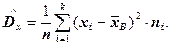Исправленная дисперсия при малых выборках n<30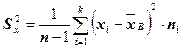 
Среднее квадратическое отклонение – это квадратный корень из выборочной дисперсии:
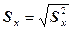– исправленное значение (n<30). 
Коэффициент вариации СV – это отношение среднего квадратического отклонения к средней величине признака, выраженное в процентах:
Коэффициент вариации – это мера относительной изменчивости случайной величины, которая позволяет сравнивать разнородные величины, например, частоту сердечных сокращений (ЧСС, уд/мин), артериальное давление (АД, мм. рт. ст.) и температуру (
) в единых единицах - процентах.
Пример 4.
Выборочная совокупность задана таблицей распределения:
|
| ||||
|
|
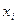
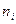
Найти выборочную дисперсию. Решение: Найдем выборочную среднюю:
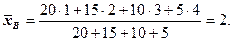
Найдем выборочную дисперсию:
Сравните 2 варьирующихся признака. Один характеризуется средней 
= 2,4 кг и средним квадратическим отклонением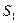 
= 0,58 кг, другой - величинами 
= 8,3 см и 
= 1,57 см. Какой признак варьируется сильнее?
Решение:
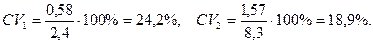
Ответ: первый, так как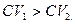 
.
Варианты заданий
Найти выборочную среднюю, выборочную дисперсию и выборочное среднее квадратическое отклонение, если совокупность задана таблицей распределения:
№ 13.1.
| |||
|
|
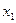
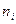
№ 13.2.
|
| ||||
|
|
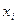
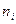
№ 13.3.
|
| ||||
|
|
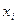
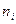
№ 13.4.
|
| |||||||
|
|
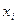
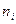
№ 13.5.
|
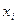
| 6,68 | 6,70 | 6,72 | 6,74 |
|
|
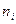
№ 13.6.
|
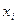
| 6,76 | 6,78 | 6,80 | 6,82 | 6,84 |
|
|
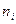
