Сумма двух событий – это такое событие, при котором появляется хотя бы одно из этих событий (А или В).
Если А и В совместные события, то их сумма А + В обозначает наступление события А или события В, или обоих событий вместе.
Если А и В несовместные события, то сумма А + В означает наступление или события А или события В.
Вероятность суммы несовместных событий равна сумме вероятностей этих событий: Р (А + В) = Р (А) + (В).
Вероятность суммы двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления:
Р (А + В) = Р (A) + P (В) – Р (АВ).
Сумма вероятностей дискретных событий, образующих полную группу, равна единице P (A 1)+ P (A 2)+…+ P (A n)=1 или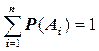 
.
Сумма вероятностей противоположных событий равна единице:
Р (А) + Р (
) = 1,
Вероятность того, что у взрослого пациента все зубы сохранились равна 0,67. Вероятность того, что некоторые зубы отсутствуют равна 0,24. Вероятность того, что он беззубый равно 0,09. Вычислить вероятность того, что у пациента несколько зубов.
Решение: Р (А + В) = Р (А) + Р (В) = 0,67 + 0,24 = 0,91.
Вероятность попадания в опухолевую клетку "мишень" первого радионуклида равна Р(A 1 ) = 0,7, а второго – Р(A 2 ) = 0,8. Найти вероятность попадания в клетку-"мишень", если бы одновременно использовались оба препарата.
Решение: Р (А1 + A2) = Р (А1) + Р (A2) – Р (А1 
A2) = 0,7 + 0,8 – 0,56 = 0,94.
В большой популяции плодовой мушки 25% мух имеют мутацию глаз, 50% – мутацию крыльев, а 40% мух с мутацией глаз имеют и мутацию крыльев. Какова вероятность того, что у мухи, наудачу выбранной из этой популяции, окажется хотя бы одна из этих мутаций?
Решение: А – событие, состоящее в том, что случайно выбранная муха имеет мутации глаз. В – событие, состоящее в том, что случайно выбранная муха имеет мутацию крыльев. Вероятность того, что муха имеет одну или обе мутации: Р (А + В) = Р (А) + Р (В) – Р (АВ). Тогда
Р (А + В) = 0,25 + 0,5 – 0,4 0,25 = 0,65.
Варианты заданий
№12.1. В коробке 30 таблеток: 10 красных, 5 желтых, 15 белых. Найти вероятность появления цветной таблетки (т.е. или красной или желтой).
№12.2. В картотеке имеются истории болезней 8 пациентов. Если наугад взять первую, затем вторую, третью и т.д. истории болезней, то какова вероятность в каждом случае изъятия нужной истории болезни? Предполагается, что искомая история болезни имеется в картотеке. Рассмотрите 2 варианта: а) взятые истории болезней не возвращаются в картотеку; б) взятые истории болезней каждый раз возвращаются в картотеку и хаотически располагаются в ней.
№12.3. В коробке имеется 7 желтых и несколько белых таблеток. Какова вероятность вытащить белую таблетку, если вероятность вытащить желтую таблетку равна 
.Сколько белых таблеток в коробке?
№12.4. Наудачу выбрано натуральное число, не превосходящее 10. Какова вероятность того, что это число является простым?
№12.5. Набирая номер телефона, абонент забыл одну цифру, и набрал ее наугад. Какова вероятность того, что набранная цифра правильная?
№12.6. Одна секретарша напечатала 5 различных писем и надписала 5 конвертов с адресами. Предположим, что она вкладывает письма в конверты случайным образом. Какова вероятность того, что ровно четыре письма будут вложены в конверты с адресами тех лиц, кому они предназначены?
№12.7. Числа от 1 до 100 записывают на полосках бумаги, которые помещают в чашу. После продолжительного встряхивания случайным образом извлекают одну полоску.
а) Какова вероятность того, что появится число, делящееся на 3?
б) Какова вероятность того, что появится число, делящееся на 3 и на 5?
№12.8. Профессор выставляет 20 разных оценок за контрольные работы 20 студентов группы и заносит их в компьютер. При распечатке ведомости из-за ошибки в компьютере оценки случайно смешались.
а) Какова вероятность того, что каждый студент получит свою верную оценку?
б) Какова вероятность того, что ровно 19 студентов получат свои верные оценки?
№12.9. В клетке содержат 6 белых и 4 серых мыши. Рассмотрим эксперимент, состоящий в случайном извлечении из клетки трех мышей.
а) Опишите пространство выборок этого эксперимента.
б) Вычислите вероятность для четырех возможных комбинаций цвета мышей (3 белых, 2 белых и 1 серая и т.д.).
№12.10. Из 20 человек, одновременно заболевших гриппом, 15 выздоровели полностью за три дня. Предположим, что из этих 20 человек случайным образом выбиралось 5. Какова вероятность того, что все 5 выздоравливают за три дня? что выздоравливают только 4 человека? что ни один не выздоравливает?
№12.11. Требуется выбрать наудачу 10 человек из группы в 10 мужчин и 10 женщин.
а) Какова вероятность того, что выбрано 10 мужчин?
б) Какова вероятность того, что выбрано больше мужчин, чем женщин?
в) Какова вероятность того, что выбрано по крайней мере 8 мужчин?
№12.12. За игрушечной пишущей машинкой с буквами A, В, С, D и Е сидит шимпанзе. Если шимпанзе печатает четыре случайных буквы, то:
а) какова вероятность того, что окажется напечатанным слово «BEAD» («шарик»)?
б) какова вероятность того, что все напечатанные буквы одинаковы?
№12.13. Участники жеребьевки тянут из ящика жетоны с номерами от 1 до 100. Найти вероятность того, что номер первого наудачу извлеченного жетона не содержит цифры 5.
№12.14. В сосуд емкостью 10 л попала ровно одна болезнетворная бактерия. Какова вероятность зачерпнуть ее при наборе из этого сосуда стакана воды (200 см3)?
№12.15. Вероятность того, что некий человек умрет на 71-м году жизни, равна 0,04. Какова вероятность того, что человек не умрет на 71-м году?
№12.16. При изучении миграций белого медведя девять медведей были помечены числами от 1 до 9. Три медведя отловлены повторно.
а) Пусть Аi обозначает событие, состоящее в том, что i -й отловленный медведь помечен четным числом. Какова вероятность Р(A 1), Р(А 2), Р(А 3)?
б) Найдите события A 1+ A 2 и A 1+ А 2+ А 3.
№12.17. В ванну, где содержатся 3 рыбы: А, В и С, время от времени помещают кусочки пищи. Каждый раз, когда бросают кусочек, рыбы конкурируют за него. Допустим, что за длительный период было установлено, что А или В добивались успеха в течение 
времени, а А или С в течение 
всего времени наблюдения. 1) Какова вероятность того, что добивается успеха рыба A? 2) Какая из рыб накормлена лучше
№12.18. В некоторую больницу поступают пациенты с четырьмя видами болезней. Многолетние наблюдения показали, что этим группам соответствуют относительные частоты 0,1; 0,4; 0,3; 0,2. Для лечения заболеваний с частотой 0,1 и 0,2 необходимо переливание крови. Какое количество больных следует обеспечить кровью, если в течение месяца поступило 1000 больных
№12.19. Опухоль-"мишень" разделена на три области. При использовании радионуклидного препарата вероятность поражения первой области равна 0,45; второй - 0,35. Найти вероятность того, что при однократном использовании радионуклид попадет либо в первую, либо во вторую область.
№12.20. Брошена игральная кость. Найти вероятность того, что выпадет четное или кратное трем число очков.
№12.21. Консультационный пункт университета получает пакеты с контрольными работами из городов A, В и С. Вероятность получения пакета из города A равна 0,6, а из города В - 0,1. Найти вероятность того, что очередной пакет будет получен из города С.
№12.22. С первого предприятия поступило 200 пробирок, из которых 190 стандартных, а со второго - 300, из которых 280 стандартных. Найти вероятность того, что наудачу взятая пробирка будет стандартной.
№12.23. На тридцати историях болезни написаны 30 двузначных чисел от 1 до 30 (их порядковые номера). Эти истории болезни лежат на полке в случайном порядке. Какова вероятность вынуть историю болезни с номером кратным 2 или 3?
№12.24. В некоторой популяции у 40% людей волосы темные, у 40% — рыжие и у 20% —светлые. В этой популяции у всех темноволосых людей глаза карие, у всех светловолосых — голубые, у одной половины рыжеволосых — голубые, а у другой — карие. Пусть А 1, А 2 и А 3 — события, состоящие в том, что у человека соответственно темные, рыжие и светлые волосы, и пусть B 1 и В 2 соответственно обозначают карие и голубые глаза.
а) Найдите Р(А 1), Р(B 1), Р(В 2) и Р(А 1 +B 2).
б) Опишите событие А 1 +A 2+ A 3. Найдите вероятность этого события.
№12.25. В популяции из 2000 плодовых мушек у 250 особей обнаруживают рецессивный признак крыла W и у 150 - рецессивный признак глаза Е. Предположим, что у 50 мушек обнаруживают оба признака. Для эксперимента по скрещиванию из популяции выбирают одну мушку.
а) Какова вероятность, что у этой мушки будет признак W? E?
б) Какова вероятность, что присутствует признак W и E?
в) Вычислите Р(
).
