Известные методы точного интегрирования дифференциальных уравнений позволяют найти решение в виде аналитической функции, однако эти методы применимы для очень ограниченного класса уравнений. Большинство уравнений, встречающихся при решении практических задач нельзя проинтегрировать с помощью этих методов.
В таких случаях используются численные методы решения, которые представляют решение дифференциального уравнения не в виде аналитической функции, а в виде таблиц значений искомой функции в зависимости от значения переменной.
Существует несколько методов численного интегрирования дифференциальных уравнений, которые отличаются друг от друга по сложности вычислений и точности результата.
Рассмотрим некоторые из них.
Метод Эйлера
Известно, что уравнение 
задает в некоторой области поле направлений. Решение этого уравнения с некоторыми начальными условиями дает кривую, которая касается поля направлений в любой точке.
Если взять последовательность точек х 0, х 1, х 2, …. и заменить на получившихся отрезках интегральную кривую на отрезки касательных к ней, то получим ломаную линию (рис. 11.1).
При подстановке заданных начальных условий (х 0, у 0 ) в дифференциальное уравнение 
получаем угловой коэффициент касательной к интегральной кривой в начальной точке
.
Заменив на отрезке [ x 0, x 1 ] интегральную кривую на касательную к ней, получаем значение
.
Производя аналогичную операцию для отрезка [ x 1, x 2 ], получаем:
.
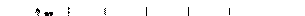
Продолжая подобные действия далее, получаем ломаную кривую, которая называется ломаной Эйлера.
Можно записать общую формулу вычислений:
.
Если последовательность точек хi выбрать так, чтобы они отстояли друг от друга на одинаковое расстояние h, называемое шагом вычисления, то получаем формулу:
Следует отметить, что точность метода Эйлера относительно невысока. Увеличить точность можно, конечно, уменьшив шаг вычислений, однако, это приведет к усложнению расчетов. Поэтому на практике применяется так называемый уточненный метод Эйлера или формула пересчета.
Суть метода состоит в том, что в формуле 
вместо значения 
берется среднее арифметическое значений f (x 0, y 0 ) и f (x 1, y 1 ). Тогда уточненное значение:
Затем находится значение производной в точке 
. Заменяя f (x 0, y 0 ) средним арифметическим значений f (x 0, y 0 ) и 
, находят второе уточненное значение у 1:
,
Затем третье:
,
и т.д. пока два последовательных уточненных значения не совпадут в пределах заданной степени точности. Тогда это значение принимается за ординату точки М 1 ломаной Эйлера.
Аналогичная операция производится для остальных значений у.
Подобное уточнение позволяет существенно повысить точность результата.
10.2. Метод Рунге – Кутта
Метод Рунге – Кутта является более точным по сравнению с методом Эйлера.
Суть уточнения состоит в том, что искомое решение представляется в виде разложения в ряд Тейлора.
Если в этой формуле ограничиться двумя первыми слагаемыми, то получим формулу метода Эйлера. Метод Рунге – Кутта учитывает четыре первых члена разложения.
.
В методе Рунге – Кутта приращения D yi предлагается вычислять по формуле:
где коэффициенты ki вычисляются по формулам:
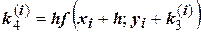
Примеры
№1. Решить методом Рунге – Кутта дифференциальное уравнение 
при начальном условии у ( 0 ) = 1 на отрезке [0; 0,5] с шагом 0,1.
Решение.
Для i = 0 вычислим коэффициенты ki:
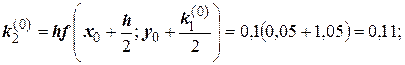
Последующие вычисления приводить не будем, а результаты представим в виде таблицы.
| i | xi | k | Dyi | yi | |
| 0,1000 | 0,1104 | ||||
| 0,1100 | |||||
| 0,1105 | |||||
| 0,1211 | |||||
| 0,1 | 0,1210 | 0,1325 | 1,1104 | ||
| 0,1321 | |||||
| 0,1326 | |||||
| 0,1443 | |||||
| 0,2 | 0,1443 | 0,1569 | 1,2429 | ||
| 0,1565 | |||||
| 0,1571 | |||||
| 0,1700 | |||||
| 0,3 | 0,1700 | 0,1840 | 1,3998 | ||
| 0,1835 | |||||
| 0,1842 | |||||
| 0,1984 | |||||
| 0,4 | 0,1984 | 0,2138 | 1,5838 | ||
| 0,2133 | |||||
| 0,2140 | |||||
| 0,2298 | |||||
| 0,5 | 1,7976 |
№2. Решим предыдущий пример методом Эйлера.
Решение.
Применяем формулу 
Производя аналогичные вычисления далее, получаем таблицу значений:
| i | ||||||
| xi | 0,0 | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 |
| yi | 1,1 | 1,22 | 1,362 | 1,528 | 1,721 |
Применим теперь уточненный метод Эйлера (точность 0,001).
| i | ||||||
| xi | 0,0 | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 |
| yi | 1,111 | 1,243 | 1,400 | 1,585 | 1,799 |
Для сравнения точности приведенных методов численного решение данного уравнения решим его аналитически и найдем точные значения функции у на заданном отрезке.
Уравнение 
является линейным неоднородным дифференциальным уравнением первого порядка. Решим соответствующее ему однородное уравнение.
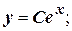
Решение неоднородного уравнения имеет вид 
.
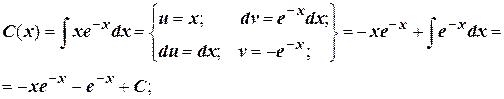
Общее решение: 
.
C учетом начального условия: 
Частное решение: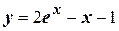 
.
Для сравнения полученных результатов составим таблицу.
| i | xi | yi | |||
| Метод Эйлера | Уточнен-ный метод Эйлера | Метод Рунге-Кутта | Точное значение | ||
| 0,1 | 1,1 | 1,111 | 1,1104 | 1,1103 | |
| 0,2 | 1,22 | 1,243 | 1,2429 | 1,2428 | |
| 0,3 | 1,362 | 1,4 | 1,3998 | 1,3997 | |
| 0,4 | 1,528 | 1,585 | 1,5838 | 1,5837 | |
| 0,5 | 1,721 | 1,799 | 1,7976 | 1,7975 |
Как видно из полученных результатов метод Рунге – Кутта дает наиболее точный ответ. Точность достигает 0,0001. Кроме того, следует обратить внимание на то, ошибка (расхождение между точным и приближенным значениями) увеличивается с каждым шагом вычислений. Это обусловлено тем что, во-первых, полученное приближенное значение округляется на каждом шаге, а во-вторых – тем что, в качестве основы вычисления принимается значение, полученное на предыдущем шаге, т.е. приближенное значение. Таким образом, происходит накопление ошибки.
Это хорошо видно из таблицы. С каждым новым шагом приближенное значение все более отличается от точного.
Варианты заданий
№11.1. Решить с помощью методов Эйлера, уточненного метода Эйлера, Рунге-Кутта и аналитически следующие дифференциальные уравнения при заданных начальных условиях, на заданном отрезке с шагом 0,2. Сравнить полученные результаты.
| № варианта | Уравнение
| Начальные условия (x 0, y 0) | Отрезок [ x 0, xк ] |
| x 0= –1, y 0= 0 | [–1, 1] | |
| x 0= 0, y 0= 2 | [0, 2] | |
| x 0= 1, y 0= 0 | [1, 3] | |
| x 0= 0, y 0= 2 | [0, 2] | |
| x 0= 0, y 0= 2 | [0, 2] | |
| x 0= 1, y 0= 1 | [1, 3] | |
| x 0= 1, y 0= 1 | [1, 3] | |
| x 0= 1, y 0= 2 | [1, 3] | |
| x 0= 0, y 0= 2 | [0, 2] | |
| x 0= 2, y 0= 0 | [2, 4] | |
| x 0= 0, y 0= 3 | [0, 2] | |
| x 0= –3, y 0= –2 | [–3, –1] | |
| x 0= –2, y 0= 1 | [–2, 0] | |
| x 0= –3, y 0= 5 | [–3, –1] | |
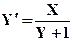
| X0= - 4,Y0= 4 | [-4,-2] | |
| X0= 2,Y0= 2 | [2,- 4] | |
| X0= 3,Y0= 0 | [3,5] | |
| X0= 0,Y0= -2 | [0,2] | |
| X0= -3,Y0= 1 | [-3,-1] | |
| X0= 2,Y0= 9 | [2,4] | |
| X0= -2,Y0= -0.4 | [-2,0] | |
| X0= - 4,Y0= -2 | [-4,-2] | |
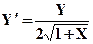
| X0= 0,Y0= 2 | [0,2] | |
| X0= 1,Y0= 1 | [1,3] |
Контрольные вопросы
1. Когда применяются численные методы решения дифференциальных уравнений?
2. Перечислите известные вам численные методы решения дифференциальных уравнений.
3. В чем заключается суть метода Эйлера?
4. В чем смысл уточненного метода Эйлера?
5. В чем смысл метода Рунге-Кутта?
6. Как рассчитать погрешность вычислений в приближенных методах?
