Численная мера степени объективности возможности наступления события называется вероятностью случайного события.
Классическое определение вероятности события А:
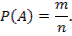
Вероятность события А равна отношению числа случаев, благоприятствующих событию А (m), к общему числу случаев (n).
У кабинета дежурного психотерапевта ожидают приема трое больных. Врачу известно по медицинским карточкам, что один из ожидающих, по фамилии Петров, болел в прошлом маниакально-депрессивным психозом. Врач интересуется этим больным, но не хочет вне очереди вызывать его в кабинет. Обозначим как событие А тот факт, что в кабинет врача входит больной Петров; как событие В обозначим то, что входит другой больной — Сидоров и как событие С — входит Иванов. События А, В и С — несовместимые и образуют полную группу (предполагается, что к врачу больные входят по одному). Так как появиться согласно очереди может равновероятно любой из больных, то до начала приема вероятность появиться первым в кабинете врача для одного из больных, в том числе для Петрова, равна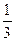 
.
При составлении команды космического корабля возникает вопрос о психологической совместимости отдельных членов экипажа. Допустим, что надо составить команду из трех человек: командира, инженера и врача. На место командира есть три кандидата a1, a2, a3; на место инженера — четыре кандидата — b1, b2, b3, b4; на место врача — два кандидата c1, c2 . Проведенная проверка показала психологическую несовместимость командира a2 с инженерами b3, b4 и с врачом c2, а также инженера b2 с врачом c2. Будем для простоты считать, что без учета фактора несовместимости все варианты составления команды равновозможны. Какова в этом случае вероятность того, что будет составлен экипаж, все члены которого психологически совместимы друг с другом.
Представим все варианты состава, при которых члены экипажа совместимы друг с другом в виде «дерева» (рис. 12.1). Число ветвей этого дерева, т. е. исходов, благоприятствующих событию А, равно 16, а общее число возможных комбинаций по правилу умножения равно произведению 4•3•2=24. Искомая вероятность 
.
Лабораторная крыса, помещенная в лабиринт, должна избрать один из пяти возможных путей. Лишь один из них ведет к поощрению в виде пище. В предположении, что крыса с одинаковой вероятностью изберет любой путь, какова вероятность выбранного пути, ведущего к пище?
Решение: 
Подбрасываются 2 монеты. Какова вероятность, что обе упадут "гербом" кверху?
Решение: 4 исхода бросания двух монет: ГГ, ГР, РГ, PP.
Пусть событие А - "выпали 2 герба" - этому событию благоприятствует один исход.
.
Подбрасываются два игральных кубика, подсчитывается сумма очков на верхних гранях. Что вероятнее - получить в сумме 7 или 8?
Решение: Обозначим события: А - "выпало 7 очков", В - "выпало 8 очков".
Событию А благоприятствуют 6 элементарных исходов: (1;6), (2;5), (3;4), (4;3), (5;2), (6;1).
Событие B благоприятствует 5 исходов: (2;6), (3;5), (4;4), (5;3), (6;2).
Всех равновозможных исходов n = 62 = 36.
Итак, Р(А) > Р(В) получить в сумме 7 очков более вероятное событие, чем получить в сумме 8 очков.
