Случайное событие
Теория вероятностей – математическая наука, изучающая закономерности случайных явлений.
Теория вероятности изучает случайные события и случайные величины.
Случайное событие – это любой факт, который в результате испытания может произойти или не произойти. Случайное событие – это результат испытания.
Испытание (опыт, эксперимент) – в этом определении понимается выполнение определенного комплекса условий, в которых наблюдается то или иное явление, фиксируется тот или иной результат. Испытание может проводиться человеком, но может осуществляться и независимо от человека. Человек в этом случае выступает в роли наблюдателя.
Событие обозначаются начальными прописными (заглавными) буквами латинского алфавита A, В, С.
1. Достоверное событие – это событие, которое в результате испытания обязательно должно произойти.
2. Невозможное событие – это событие, которое в результате испытания вообще не может произойти.
События называются несовместными, если наступление одного из них исключает появление другого. В противном случае события – совместные.
Противоположные события: два события A и 
называются противоположными, если непоявление одного из них в результате данного испытания влечет появление другого. ( читается "не А").
Комбинаторика
Комбинаторика — раздел математики, изучающий вопросы о том, сколько комбинаций определенного типа можно составить из данных предметов (элементов). Как при решении задач с использованием классического определения вероятности, так и в дальнейшем нам понадобятся некоторые формулы комбинаторики. Приведем наиболее употребительные из них.
Размещениями из n различных элементов по m элементов (m ≤ n) называются комбинации, составленные из данных n элементов по m элементов, которые отличаются либо самими элементами, либо порядком следования элементов.
Например, из трех элементов a, b, c можно составить по два элемента следующие размещения: ab, ас, bc, ba, ca, cb.
Число различных размещений из n элементов по m элементов определяется с помощью формулы
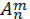= n (n – 1)(n – 2)....(n – m +1) = 
.
Сколько можно составить сигналов из 6 флажков различного цвета, взятых по 2? Искомое число сигналов 
= 6•5 = 30.
Перестановками из n различных элементов называются размещения из этих n элементов по n.
Как видно из определений 1 и 2, перестановки можно считать частным случаем размещений при m = n. Следовательно, число всех перестановок из п элементов вычисляется по формуле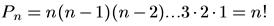 
Перестановки состоят из одних и тех же различных элементов и отличаются друг от друга только порядком их следования.
Для лечения заболевания применяют три лекарства. Полагают, что последовательность, в которой применяют лекарства, оказывает существенное влияние на результат лечения. Сколько имеется различных порядков назначения этих лекарств?
Имеется 
различных порядков назначения трех лекарств.
Сочетаниями из n различных элементов по m элементов называются комбинации, составленные из данных n элементов по m элементов, которые отличаются хотя бы одним элементом.
Отметим разницу между сочетаниями и размещениями: в сочетаниях не учитывается порядок элементов.
Число сочетаний из n элементов по m элементов вычисляется по формуле
В лабораторной клетке содержат трех белых и трех коричневых мышей. Найти число способов выбора двух мышей, если они могут быть любого цвета.
В данном случае цвет не существен. Поэтому имеется
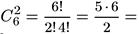15 способов, которыми две мыши можно выбрать из шести.
При решении задач комбинаторики используют следующие правила:
Правило суммы. Если некоторый объект А может быть выбран из множества объектов m способами, а другой объект В может быть выбран n способами, то выбрать либо A либо В можно m + n способами.
Правило произведения. Если объект А можно выбрать из множества объектов m способами и после каждого такого выбора объект В можно выбрать n способами, то пара объектов (А, В) в указанном порядке может быть выбрана m * n способами.
