При изучении одного экономического объекта (региона, муниципального образования, предприятия и т.п.) исследователь обычно располагает только временными данными. Это может быть информация за несколько лет, кварталов или месяцев. Могут также исследоваться и связи между биржевыми котировками разных товаров, ценных бумаг и валют по результатам торгов за несколько дней (см. тесты 2.3, 2.7, 2.10). Во всех указанных случаях регрессионные модели строятся по временным рядам переменных.
Экономическим временным рядом называется совокупность значений экономической переменной за несколько последовательных, как правило, равноотстоящих друг от друга моментов или интервалов времени. В первом случае временной ряд является моментным, во втором — интервальным.
Отдельные значения временного ряда называются уровнями. Временные ряды могут быть образованы не только абсолютными значениями переменной, но и средними за некоторый период или относительными величинами. Временные данные для построения регрессионной модели представляются в табличной форме (табл. 3.2). Параметры модели оцениваются обычным методом наименьших квадратов.
| Таблица | 3.2 |
| Исходные данные для построения модели множественной регрессии по временным рядам экономических переменных |
| Номер момента (интервала) времени t | Значение (уровень) результата Y | Набор факторов и их значения (уровни) | |||||
| X 1 | X 2 | … | Xj | … | Xp | ||
| y 1 | x 11 | x 12 | … | x 1 j | … | x 1 p | |
| y 2 | x 21 | x 22 | … | x 2 j | … | x 2 p | |
| … | … | … | … | … | … | … | … |
| t | yt | xt 1 | xt 2 | … | xtj | … | xtp |
| … | … | … | … | … | … | … | |
| n | yn | xn 1 | xn 2 | … | xnj | … | xnp |
Особенностями такой модели является то, что временные ряды переменных объекта могут иметь общую тенденцию, что, в свою очередь, может привести к «ложной» корреляции между переменными, мультиколлинеарности факторов и другим негативным последствиям. Наличие общей тенденции во временных рядах означает, что на результат Y и факторы X 1, X 2, …, Xp оказывает влияние фактор времени, который в модели (3.2) непосредственно не учтен.
Для учета фактора времени целесообразно построить модель, включающую в качестве независимой переменной номер момента (интервала) времени t:
 .
| (3.23) |
Параметр c1 показывает средний абсолютный прирост результата Y за один временной промежуток из-за наличия линейной тенденции во временном ряду Y. Параметры модели (3.23) оцениваются обычным методом наименьших квадратов, в результате чего получают уравнение регрессии
 ,
| (3.24) |
где с 1 — оценка параметра модели c1 по статистическим данным.
Значимость коэффициента при факторе времени проверяется по t ‑критерию Стьюдента. Если этот коэффициент окажется либо статистически незначимым (
), либо неинформативным (
), то его следует исключить из модели.
При построении регрессионной модели по временным рядам переменных следует тщательно проверить выполнение предпосылок метода наименьших квадратов (см. § 3.8).
Широкое распространение на практике получили трендовые модели экономического прогнозирования. В таких моделях независимой переменной является только фактор времени t, который условно заменяет всю совокупность причинных факторов, влияющих на результат Y. Построение трендовых моделей основано на использовании метода экстраполяции.
Экстраполяцией экономических процессов называется продление на будущее тенденции, наблюдающейся во временном ряду исследуемой экономической переменной Y. При экстраполяции исходят из предположения о возможности представления уровней yt временного ряда переменной Y в виде суммы компонент, отражающих соответственно закономерность (тренд) и случайность (отклонения от тренда) развития процесса:
 ,
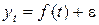| (3.25) |
где f (t) — функция тренда — плавная кривая, аппроксимирующая временной ряд переменной Y; e — случайная (остаточная)компонента; t =1, 2, …, n.
Уравнение регрессии трендовой модели в общем виде представляется как
 .
| (3.26) |
Основной задачей экстраполяции является выявление закономерности в формировании уровней временного ряда и оценка степени влияния на них случайных факторов. Выявленные закономерности могут быть использованы для прогнозирования значений исследуемой переменной в будущем, а учет случайности позволяет оценить вероятность и возможную величину отклонения фактического значения переменной от предсказанного.
Трендовые модели являются по своей сути парными моделями регрессии, поэтому к ним могут применяться все рассмотренные в главе 2 методы. Предварительно проводят визуальный анализ графика временного ряда, что дает представление о закономерности формирования уровней и позволяет выбрать модель, наиболее подходящую для описания этой закономерности. Чаще всего на практике используются линейное и показательное уравнения регрессии:
 ;
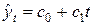| (3.27) | |
 ,
| (3.28) |
параметры которых имеют содержательную экономическую интерпретацию.
Параметр с 0 можно рассматривать как среднее значение переменной Y в момент (интервал) времени, предшествующий первому уровню, т. е. при t =0 («ближайшее прошлое»).
Коэффициент c 1 линейной модели является средним абсолютным приростом переменной Y во временном ряду и показывает, на сколько в среднем возрастает Y за один временной промежуток. Отрицательное значение c 1 свидетельствует о тенденции уменьшения переменной Y во времени.
Показатель степени c 1 показательной модели является средним коэффициентом роста. Он показывает, во сколько раз в среднем возрастает переменная Y за один временной промежуток. Если значение c 1 находится в интервале от 0 до 1, то это свидетельствует об уменьшении Y в среднем.
Если тенденция во временном ряду изменяет свое направление с возрастающей на убывающую или, наоборот, — с убывающей на возрастающую, то выбирают полиноминальную модель второго порядка. Полиномы более высоких степеней применяют в обоснованных случаях.
После построения трендовой модели следует проверить статистическую значимость уравнения регрессии и оценить точность модели. Во временном ряду остатков не должна присутствовать автокорреляция, а их закон распределения должен соответствовать нормальному (см. § 3.8) Если приятая модель удовлетворяет требованиям качества, то ее можно использовать для прогнозирования значений исследуемой переменной в ближайшем будущем. С этой целью строятся точечный и интервальный прогнозы.
Точечный прогноз переменной Y определяется путем подстановки в уравнение регрессии номера временного промежутка 
, соответствующего требуемому периоду упреждения k:
 .
| (3.29) |
Например, точечный прогноз на k шагов вперед по линейной модели
 .
| (3.30) |
Точечный прогноз является лишь средним прогнозируемым значением исследуемой переменной. Для учета случайных колебаний строят интервальный прогноз. В случае линейной модели используются либо формулы, приведенные в 2.5, либо следующее выражение:
 ,
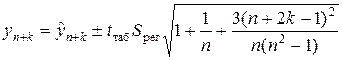| (3.31) |
где S рег — стандартная ошибка регрессии (2.8); t таб — табличное значение t ‑критерия Стьюдента для уровня значимости a и числа степеней свободы 
(см. приложение 3).
Считается, что если модель удовлетворяет требованием качества, то с доверительной вероятностью 
фактическое значение прогнозируемой переменной Y попадет в доверительный интервал (3.31). Заметим, что чем большее значение имеет период упреждения k, тем менее точным является прогноз.
Если рост исследуемой переменной является желательным (например, прибыль предприятия), то верхнюю границу интервального прогноза можно рассматривать как оптимистический вариант развития ситуации, а нижнюю — как пессимистический. И, наоборот, для такого показателя как, например, издержки, оптимистический вариант развития соответствует нижней границе, а пессимистический — верхней.
