Оценка значимости уравнения регрессии

После получения уравнения регрессии необходимо проверить его значимость, т.е. установить соответствует ли принятая модель фактическим данным и достаточно ли включено в нее факторов для объяснения изменения зависимой переменной Y. Одним из способов такой проверки является проверка выполнения условия (2.2). Более универсальным является метод дисперсионного анализа, сущность которого заключается в разложении суммы квадратов отклонений фактических значений результата Y от своего среднего на компоненты, соответствующие предполагаемым источникам, вызывающим эти отклонения:

,

(2.9)

где — общая сумма квадратов отклонений; — сумма квадратов отклонений, вызванных регрессией (факторная сумма); 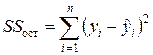— сумма квадратов отклонений, обусловленных влиянием неучтенных и случайных факторов (остаточная сумма).

Уравнение (2.9) вытекает из соотношения

,

(2.10)

после возведения в квадрат его обеих частей и суммирования для всех n наблюдений (рис. 2.3).

Каждая из сумм квадратов SS _общ, SS _рег, SS _ост связана со своим числом степеней свободы, которое показывает, сколько независимых элементов информации, получающихся из n наблюдений результата Y, требуется для образования данной суммы квадратов отклонений.

Так, для суммы SS _общ требуется 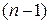независимый элемент, ведь после расчета среднего n наблюдений Y, независимо варьировать можно лишь 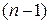отклонений от , из-за того, что . Поэтому число степеней свободы SS _общ равно .

Факторная сумма SS _рег для парной регрессии имеет одну степень свободы (df _рег=1), так как для ее образования требуется знать лишь значение углового коэффициента b ₁, что видно из соотношения

.

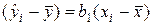(2.11)

Число степеней свободы остаточной суммы SS _ост равно разности между df _общи df _рег, и в случае парной регрессии: .

Отношение суммы квадратов отклонений SS к соответствующему числу степеней свободы df определяет средний квадрат отклонений MS, показывающий, какая часть этой суммы приходится на одну степень свободы. Обычно результаты дисперсионного анализа уравнения регрессии представляют в виде таблицы (табл. 2.1).

Уравнение регрессии признается статистически значимым на уровне значимости a, если выполняется условие

,

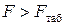(2.12)

где F — F -статистика уравнения (см. табл. 2.1); F _таб — табличное значение F ‑критерия Фишерадля заданного уровня значимости a и чисел степеней свободы числителя и знаменателя (приложение 4); n — число наблюдений; m — число коэффициентов уравнения регрессии, включая свободный коэффициент b ₀ (для линейной парной модели m =2).

рис. 2.3. Схема дисперсионного анализа уравнения регрессии

Источник вариации результата Y	Число степеней свободы (df)	Сумма квадратов отклонений (SS)	Средний квадрат (MS)	F-статистика
Регрессия
Остаток				—
Итого (общая вариация Y)			—	—

Если неравенство (2.12) не выполняется, то считается, что достоверно неизвестно, какими причинами вызвана вариация результата Y — регрессией на X, либо неучтенными или случайными факторами. Уравнение регрессии в этом случае лишено смысла и непригодно для практического использования.

Компьютерные программы автоматизации статистического анализа вместе со значением F -статистики обычно приводят и вероятность того, что это значение получилось случайным образом (в EXCEL — «Значимость F»). Уравнение регрессии значимо, если эта вероятность не превышает заданный уровень значимости a (обычно a=0,05).