Перед построением модели множественной регрессии вычисляются парные коэффициенты линейной корреляции между всеми исследуемыми переменными Y, X 1, X 2, …, Xp, и из них формируется матрица:
 .
| (3.10) |
Данная матрица симметрична относительно главной диагонали, так как 
, 
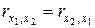и т.д. Поэтому программные средства статистического анализа обычно приводят только половину матрицы, как правило, нижнюю.
Ситуация, когда два фактора связаны между собой тесной линейной связью (парный коэффициент корреляции между ними превышает по абсолютной величине 0,8), называется коллинеарностью факторов. Коллинеарные факторы фактически дублируют друг друга в модели, существенно ухудшая ее качество. Поэтому один из них целесообразно исключить из рассмотрения. Какой из факторов следует оставить в модели, а какой отбросить, решают, в первую очередь, исходя из сущности исследуемого явления и желаемого вида модели. Если с экономической точки зрения ни одному из факторов нельзя отдать предпочтение, то обычно в модели оставляют тот из них, который имеет больший коэффициент корреляции с зависимой переменной Y.
Пусть, например, факторы Xj и Xk связаны друг с другом тесной линейной связью (
), а коэффициенты корреляции между ними и результатом Y соотносятся как 
. При прочих равных условиях, в модели целесообразно оставить фактор Xj, а фактор Xk исключить из нее.
Иногда может быть полезно построить модель регрессии с обоими коллинеарными факторами, а затем исключить из рассмотрения фактор, коэффициент уравнения регрессии при котором имеет меньшую по абсолютной величине t -статистику.
Наибольшие трудности возникают при наличии мультиколлинеарности факторов, когда тесной связью одновременно связаны несколько факторов. В этом случае вариация факторов в исходных данных перестает быть независимой, и нельзя оценить влияние каждого из факторов на результат Y по отдельности. Уравнение регрессии с мультиколлинеарностью факторов обычно не имеет реального смысла, так как некоторые из его коэффициентов могут иметь неправильные с экономической точки зрения знаки и значения. Эти коэффициенты, как правило, имеют большие стандартные ошибки и незначимы по t ‑критерию Стьюдента, в то время как в целом уравнение регрессии может оказаться значимым по F -критерию Фишера и иметь высокое значение множественного коэффициента детерминации R 2. Небольшое изменение исходных данных (например, добавление новых наблюдений) может привести к существенному изменению значений таких коэффициентов.
Основным способом устранения мультиколлинеарности является исключение из модели одного или нескольких факторов по рассмотренному выше принципу. Другой способ состоит в преобразовании факторов, при котором уменьшается корреляция между ними.
