I Разложение функции 
Эта функция имеет производных всех порядков при любом х:  (n=1,2,3,…)
(n=1,2,3,…)
Проверим выполнение условий теоремы 2:
если взять любой промежуток  , то в нем верна оценка
, то в нем верна оценка 
(т. е. для всех значений х модули всех производных ограничены одним и тем же числом  ).
).
Поэтому по теореме 2 функция  разлагается в сходящийся к ней ряд Маклорена в любом промежутке
разлагается в сходящийся к ней ряд Маклорена в любом промежутке  , т. е. иначе говоря, при всех х (всюду).
, т. е. иначе говоря, при всех х (всюду).
Найдем коэффициенты ряда:

таким образом, при любых х верно разложение:

Пример 6.2.31. Разложить в ряд Маклорена функцию  ; указать интервал сходимости
; указать интервал сходимости
Решение  ,
, 
II Разложение функции 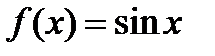
Она имеет производные всех порядков:
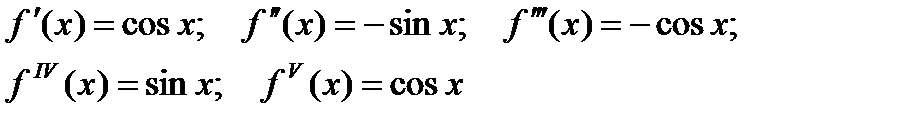
Очевидно, условия теоремы 2 выполняются: при всех х и n производная функции  по модулю не превосходит единицы.
по модулю не превосходит единицы.
Следовательно,  разлагается в ряд Маклорена и разложение справедливо при всех х.
разлагается в ряд Маклорена и разложение справедливо при всех х.
Найдем коэффициенты ряда:
 Таким образом, при любых х верно разложение:
Таким образом, при любых х верно разложение:
(*)  ,
, 
В ряде присутствуют только нечетные степени х; это естественно, т. к.  - нечетная функция.
- нечетная функция.
Можно считать равенство (*) определением функции  , т. к. радиус сходимости ряда равен бесконечности, и, следовательно, сумма ряда определена и непрерывна на всей числовой оси. Эту сумму и можно по определению считать функцией
, т. к. радиус сходимости ряда равен бесконечности, и, следовательно, сумма ряда определена и непрерывна на всей числовой оси. Эту сумму и можно по определению считать функцией  такое определение
такое определение  не связано с геометрическим построением, с которыми эта функция так тесно связана в школьном курсе математики.
не связано с геометрическим построением, с которыми эта функция так тесно связана в школьном курсе математики.
III Разложение функции 
Разложение в ряд этой функции можно получить так же, как и для 
Но можно получить его путем дифференцирования разложения для  :
:
 ,
, 
Пример 6.2.32. Разложить функцию  в ряд по степеням х.
в ряд по степеням х.
Решение: 

IV Разложение функции 
Мы должны получить разложение логарифмической функции (в ряд Маклорена) по степеням х. Надо, чтобы сама функция и все ее производные имели смысл при х=0.
Если взять  ,
,  ,
,  и т. д.
и т. д.
Как видим, f(0) и f(n)(0) при всяком n лишены смысла. Поэтому рассматриваем функцию  Эта функция и все ее производные определены при х=0.
Эта функция и все ее производные определены при х=0.
Итак,  ;
; 
Разложим эту функцию в ряд, используя возможность почленного интегрирования степенных рядов.
Найдем  ; производная может быть разложена в ряд Маклорена, т. к. дробь
; производная может быть разложена в ряд Маклорена, т. к. дробь  может рассматриваться как сумма геометрической прогрессии (убывающей) при
может рассматриваться как сумма геометрической прогрессии (убывающей) при 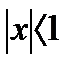 (знаменатель прогрессии q=-x):
(знаменатель прогрессии q=-x):

где  (радиус сходимости ряда)
(радиус сходимости ряда)
Проинтегрируем этот степенной ряд почленно в промежутке  , где
, где 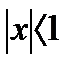 (интервал интегрирования не выходит за пределы интервала сходимости ряда):
(интервал интегрирования не выходит за пределы интервала сходимости ряда):

 ,
, 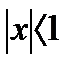
Сохраняется ли это равенство при х=±1?
При х=±1 теряет смысл функция  , поэтому равенство при х=-1 лишено смысла.
, поэтому равенство при х=-1 лишено смысла.
При х=1 сохраняет смысл функция  , она обращается в число
, она обращается в число  Ряд
Ряд  сходится (по признаку Лейбница).
сходится (по признаку Лейбница).
Остается проверить, имеет ли место равенство:
(*) 
Из рассмотренных выше рассуждений справедливость равенства (*) пока еще не вытекает, т. к. доказали только, что разложение функции  верно при
верно при 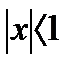 .!Для проверки равенства (*) проведем оценку остаточного члена при х=1:
.!Для проверки равенства (*) проведем оценку остаточного члена при х=1:
Закон образования производных найти легко:


Остаточный член (в форме Лагранжа):

 найдем
найдем  при х=1:
при х=1:

Т. к.  , то при
, то при  стремится к нулю:
стремится к нулю:  при
при  . А это означает (теорема 1), что ряд (*) сходится и имеет своей суммой число
. А это означает (теорема 1), что ряд (*) сходится и имеет своей суммой число  , т. е. равенство (*) верно.
, т. е. равенство (*) верно.
Итак,  ,
, 
V Разложение функции 
 ; эту дробь при
; эту дробь при  можно рассматривать как сумму убывающей геометрической прогрессии со знаменателем
можно рассматривать как сумму убывающей геометрической прогрессии со знаменателем  :
:

Интегрируя в пределах от 0 до х, где  , получаем:
, получаем:  ; откуда имеем:
; откуда имеем:

 ,
,  (что будет показано ниже)
(что будет показано ниже)
Проверим, не сохраняется ли это равенство и при х=±1.
При х=-1 – самостоятельно!
При х=1: ряд принимает вид: 
который сходится (по теореме Лейбница).
!Остается проверить, имеет ли место равенство:
(*) 
Для этого поступим следующим образом:
 т. е. приостанавливаемся на (n+1) члене!!!
т. е. приостанавливаемся на (n+1) члене!!!
Интегрируем это равенство (конечное число слагаемых) в промежутке от 0 до 1:

т.к.  при
при 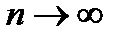 , то, следовательно правая часть
, то, следовательно правая часть  при
при 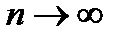 (в силу равенства (**)):
(в силу равенства (**)):  при
при 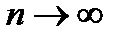 ; это и означает, что сумма ряда (*)
; это и означает, что сумма ряда (*)  , т. е. равенство верно.
, т. е. равенство верно.
Комплексные числа
КОМПЛЕКСНЫЕ ЧИСЛА И ДЕЙСТВИЯ НАД НИМИ
Число  , где
, где  и
и  - действительные числа, а
- действительные числа, а  - так называемая мнимая единица, называется
- так называемая мнимая единица, называется  комплексным числом. Действительные числа
комплексным числом. Действительные числа  и
и  называются соответственно действительной и мнимой частями комплексного числа
называются соответственно действительной и мнимой частями комплексного числа  и обозначаются:
и обозначаются: 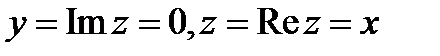 -
-  есть действительное число; если
есть действительное число; если  , а
, а  , то число
, то число  называется числом мнимым.
называется числом мнимым.
Два комплексных числа  и
и  считаются равными, если равны их действительные и мнимые части, т. е.
считаются равными, если равны их действительные и мнимые части, т. е. 
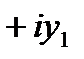 =
= 

 при
при  и
и 
Будем изображать комплексное число  с помощью точки на плоскости, абсцисса которой равна
с помощью точки на плоскости, абсцисса которой равна  , а ордината
, а ордината  . Тогда всякое комплексное число изобразится с помощью определенной точки, так называемой комплексной плоскости.
. Тогда всякое комплексное число изобразится с помощью определенной точки, так называемой комплексной плоскости.
Положение точки, изображающей комплексное число z, можно определить также с помощью полярных координат r и φ будем называть соответственно модулем и аргументом комплексного числа z: r =|z|; φ = Arg z. Из определения модуля и аргумента следует, что если  , то x = r cos φ =|z | cos (Arg z); y =r sinφ=|z| sin(Arg z);
, то x = r cos φ =|z | cos (Arg z); y =r sinφ=|z| sin(Arg z);

tgφ 
 (при х
(при х  ).
).
Заметим, что величина j=Arg z имеет бесчисленное множество значений, отличающихся одно от другого на целое, кратное 2p. Если величину одного из углов обозначить через j0, то совокупность величин всех углов запишется выражением
Arg z=j0+2pk (k=0,±1, ±2,…).
Значение j=Arg z, принадлежащее промежутку ]- p,p[, называется главным и обозначается j0=arg z, т.е -p<arg z£p.
Следовательно,
Arg z= Arg z++2pk (k=0,±1, ±2,…).
Зная действительную х и мнимую у части комплексного числа z и пользуясь тем, что tg (arg z)=y/x, можно вычислить arg z по формуле

Числу 0 не приписывается какое - либо значение аргумента.
Всякое комплексное число, отличное от нуля, можно представить ь в тригонометрической форме
z=x+iy=rcosj+irsinj=r(cosj+isinj).
Замечание 1.1. С помощью формулы Эйлера eij=cosj+isinj можно представить комплексное число в показательной форме:
z= r e ij .
Комплексные числа z=x+iy и  называют взаимно-сопряженными. При этом
называют взаимно-сопряженными. При этом  .
.
Сложение, вычитание и умножение комплексных чисел производят по правилам сложения, вычитания и умножения алгебраических многочленов, полагая при этом i2=-1, i3=-i, i4=1,…
При сложении и вычитании комплексных чисел отдельно складываются и вычитаются их действительные и мнимые части:
(x1+iy1)±(x2+iy2)=(x1+x2)+i(y1+y2).
Умножение:
(x1+iy1) (x2+iy2)=(x1x2-y1y2)+i(x1y2+x2y1).
Деление определяется как действие, обратное умножению.
Деление удобно производить следующим образом; сначала умножить делимое и делитель на число, сопряженное делителю, после чего делитель станет действительным числом  , а затем произвести деление действительной и мнимой частей отдельно;
, а затем произвести деление действительной и мнимой частей отдельно;

Если воспользоваться тригонометрической формой записи чисел
z1=r1(cosj1+isinj1); z2=r2(cosj2+isinj2);
получим
z1 z2=r1 r2 [(cos(j1+j2)+isin(j1+j2)], (6.3.1)
т.e, при умножении комплексных чисел их модули перемножаются, а аргументы складываются:
 . (6.3.2)
. (6.3.2)
Из правила умножения следует правило возведения в целую положительную степень: если
z=r(cosj+isinj), то zn=rn(cosnj+isin nj). (6.3.3)
Нетрудно убедиться, что формула справедлива и при целом отрицательном n.
Извлечь корень целой положительной степени n из числа z - значит найти такое число  , n-я степень которого равна z.
, n-я степень которого равна z.






