Решение уравнений и систем
В задачах 9.1.1. - 9.1.5. все решения должны быть проиллюстрированы соответствующими графиками.
9.1.1 Найти наименьший положительный корень уравнения:
9.1.2 Найти больший корень уравнения:
9.1.3 Найти все корни уравнения:
9.1.4 Найти все корни уравнения:
9.1.5 Найти корень уравнения с точностью 10-6:
9.1.6 Найти все корни системы нелинейных уравнений:
Для построения окружности воспользоваться ее параметрическим представлением x = R× cos(t); y = R × sin(t); 0 £ t £ 2 p.
9.1.7 Решить систему нелинейных уравнений:
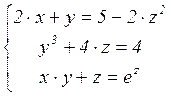
Нахождение экстремумов функций
В задачах 9.2.1. - 9.2.7. все решения должны быть показаны на соответствующих графиках.
9.2.1 Найти минимум функции f(x) на интервале [ - 4; 0 ]:
9.2.2 Найти минимум функции f(x) на интервале [ 0; 4 ]:
9.2.3 Найти максимум функции f(x) на интервале [ -1; 1 ]:
9.2.4 Найти максимум функции f(x) на интервале [ -2; 4 ]:
9.2.5 Найти максимум и минимум функции
9.2.6 Найти минимум функции f(x, y) в области 0.4 £ x £ 2.6, -0.2 £ y £ 1
9.2.7 Найти максимум функции f(x, y) в области -0.2 £ x £ 0.4, 0 £ y £ 0.5
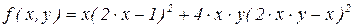
Интерполяция данных
9.3.1 Исходные данные имеют вид:
| X | 0.5 | 1.2 | 2.6 | 4.3 | 4.9 | 6.8 | 8.7 |
| Y | 4.1 | 2.4 | 4.3 | 3.6 | 5.2 |
С помощью линейной интерполяции вычислить значение y, если x = 3.45. Построить график, отображающий линейную интерполяцию для -1 £ x £ 10, отложив по оси ординат величину interp(X, Y, x). Показать на графике исходные данные.
9.3.2 С помощью сплайн-интерполяции вычислить значение y, если x = 3.45, для данных из задачи 9.3.1.
Построить график, отображающий сплайн-интерполяцию для -1 £ x £ 10. Показать на графике исходные данные.
9.3.3 С помощью полиномиальной интерполяции вычислить значение y, если x = 3.45, для данных из задачи 9.3.1.
Построить график, отображающий сплайн-интерполяцию для 0.5 £ x £ 9. Показать на графике исходные данные.
9.3.4 Функция f (x,y) представлены в виде таблицы:
| y x | 1.2 | 1.4 | 1.6 | 1.8 | 2.0 | 2.2 |
| 0.3 | 0.738 | 1.574 | 2.746 | 4.302 | 6.29 | 8.758 |
| 0.6 | - 0.072 | 0.584 | 1.576 | 2.952 | 4.76 | 7.048 |
| 0.9 | - 0.702 | - 0.226 | 0.586 | 1.782 | 3.41 | 5.518 |
| 1.2 | - 1.152 | - 0.856 | - 0.224 | 0.792 | 2.24 | 4.168 |
| 1.5 | - 1.422 | - 1.306 | - 0.854 | - 0.018 | 1.25 | 2.998 |
| 1.8 | - 1.512 | - 1.576 | - 1.304 | - 0.648 | 0.44 | 2.008 |
Интерполировать кубическим сплайном функцию f (x,y) в точке (1, 1.5). Построить интерполяционную поверхность.
9.3.5 Вычислить значение функции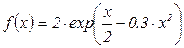 
на интервале
[ -2; 1 ] и осуществить линейное предсказание ее поведения на интервале [ 1; 2 ].
Результат показать на графике.
Аппроксимация данных
В задачах 9.4.1 - 9.4.7 нужно аппроксимировать данные указанными зависимостями (вычислить их коэффициенты) и построить графики, на которых следует отобразить как сами данные, так и аппроксимирующие кривые.
| 9.4.1 y = A × x + B |
|
| 9.4.2 y = A0 + A1 · x + A2 · x2 + A3 · x3 |
|
В задачах 9.4.3 - 9.4.5 указанные зависимости необходимо сначала путем преобразований и замены переменных свести к линейному виду.
9.4.3 
|
|
9.4.4 
|
|
9.4.5 
|
|
9.4.6 
|
|
9.4.7 
|
|
9.4.8 Решить задачу 9.4.3, минимизируя сумму квадратов отклонений аппроксимирующей функции A· exp (B/x) от исходных данных с помощью встроенной функции minerr.
