ѕриклад 1. ≈лектрон, початковою швидк≥стю €кого можна знехтувати, пройшов прискорювальну р≥зницю потенц≥ал≥в U. «найти довжину хвил≥ де Ѕройл€ дл€ двох випадк≥в: 1) U1 = 51 B; 2) U2 = 510 к¬.
ƒано:
U1 = 51 B
U2 = 510 к¬ = 5,1.10 5 ¬
____________________
 Ц?
Ц? 
–озвТ€зуванн€. ƒовжина хвил≥ де Ѕройл€  дл€ частинки залежить в≥д њњ ≥мпульсу р ≥ визначаЇтьс€ формулою
дл€ частинки залежить в≥д њњ ≥мпульсу р ≥ визначаЇтьс€ формулою
 , (1)
, (1)
де h Ц пост≥йна ѕланка.
≤мпульс частинки можна визначити, €кщо в≥дома њњ к≥нетична енерг≥€ ≈к. «вТ€зок ≥мпульсу з к≥нетичною енерг≥Їю р≥зний дл€ нерел€тив≥стського випадку (коли к≥нетична енерг≥€ частинки багато менша енерг≥њ њњ спокою) ≥ дл€ рел€тив≥стського випадку (коли к≥нетична енерг≥€ зб≥гаЇтьс€ за величиною з енерг≥Їю спокою частинки).
” нерел€тив≥стському випадку
p=  , (2)
, (2)
де m0 Ц маса спокою частинки.
” рел€тив≥стському випадку
p=  , (3)
, (3)
де ≈0 = m0c2 Ц енерг≥€ спокою частинки;
с Ц швидк≥сть св≥тла у вакуум≥.
‘ормула (1) з урахуванн€м сп≥вв≥дношень (2) ≥ (3) запишетьс€:
- у нерел€тив≥стському випадку
 , (4)
, (4)
- у рел€тив≥стському випадку
 . (5)
. (5)
«р≥вн€Їмо к≥нетичн≥ енерг≥њ електрона, €кий пройшов задан≥ в умов≥ задач≥ р≥зниц≥ потенц≥ал≥в U1 = 51 ¬ и U2 = 510 к¬, з енерг≥Їю спокою електрона й, залежно в≥д цього, вир≥шимо, €ку з формул (4) або (5) варто застосувати дл€ обчисленн€ довжини хвил≥ де Ѕройл€.
як в≥домо, к≥нетична енерг≥€ електрона, €кий пройшов прискорювальну р≥зницю потенц≥ал≥в U, дор≥внюЇ
Eк = qU.
” першому випадку
≈к = q1U = 51 еB = 0,51.10-4 ћe¬.
ќтже, у цьому випадку можна застосувати формулу (4). ƒл€ спрощенн€ розрахунк≥в пом≥тимо, що ≈к = 10-4 moc2. ѕ≥дставивши цей вираз у формулу (4), перепишемо њњ у вигл€д≥

”рахувавши, що  Ї комптон≥вська довжина хвил≥
Ї комптон≥вська довжина хвил≥  , одержимо
, одержимо
 .
.
ќск≥льки  = 2,43 пм, то
= 2,43 пм, то
 пм = 171 пм.
пм = 171 пм.
” другому випадку к≥нетична енерг≥€
Eк = qU2 = 510 ке¬ = 0,51 ће¬,
тобто дор≥внюЇ енерг≥њ спокою електрона. ” цьому випадку необх≥дно застосувати рел€тив≥стську формулу (5). ”рахувавши, що ≈к = 0,51ћэ¬ = = moc2, за формулою (5) знайдемо
 ,
,
ѕ≥дставивши значенн€ й виконавши необх≥дн≥ розрахунки, одержимо
 1,40 пм.
1,40 пм.
ѕриклад 2. ≥нетична енерг≥€ електрона в атом≥ водню не перевищуЇ величину 10е¬. ¬икористовуючи сп≥вв≥дношенн€ невизначеностей, оц≥нити м≥н≥мальн≥ розм≥ри атома.
ƒано:
≈к = 10 е¬
_________
lmin Ц?
–озвТ€зуванн€. —п≥вв≥дношенн€ невизначеностей дл€ координати й ≥мпульсу записують так:
 / 2,
/ 2,
де  Ц невизначен≥сть ≥мпульсу частинки (електрона);
Ц невизначен≥сть ≥мпульсу частинки (електрона);
 Ц невизначен≥сть координати частинки (у цьому випадку електрона);
Ц невизначен≥сть координати частинки (у цьому випадку електрона);
 Ц пост≥йна ѕланка (h под≥лена на 2
Ц пост≥йна ѕланка (h под≥лена на 2  ).
).
≤з сп≥вв≥дношенн€ невизначеностей випливаЇ, що чим точн≥ше визначаЇтьс€ положенн€ частинки в простор≥, тим б≥льше невизначеним стаЇ ≥мпульс, а отже, ≥ енерг≥€ частинки. Ќехай атом маЇ л≥н≥йн≥ розм≥ри l, тод≥ електрон атома буде перебувати десь у межах област≥ з невизначен≥стю
|
|
|
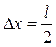 .
.
¬ цьому випадку сп≥вв≥дношенн€ невизначеностей можна записати у вигл€д≥
 ,
,
зв≥дки

‘≥зично розумна невизначен≥сть ≥мпульсу  не повинна перевищувати значенн€ самого ≥мпульсу p, тобто
не повинна перевищувати значенн€ самого ≥мпульсу p, тобто  .
.
≤мпульс р пов'€заний з к≥нетичною енерг≥Їю ≈к сп≥вв≥дношенн€м
р = 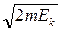 .
.
«ам≥нимо  р значенн€м
р значенн€м  (така зам≥на не зб≥льшить
(така зам≥на не зб≥льшить  ). ѕерейдемо до р≥вност≥
). ѕерейдемо до р≥вност≥
lmi n =  .
.
ѕ≥дставивши числов≥ значенн€ й виконавши обчисленн€, одержимо
lmi n =  м = 1,16.10-10 м = 116 пм.
м = 1,16.10-10 м = 116 пм.
ѕриклад 3. ’вильова функц≥€  описуЇ основний стан частинки в неск≥нченно глибокому пр€мокутному €щику шириною l. ќбчислити ≥мов≥рн≥сть знаходженн€ частинки в малому ≥нтервал≥
описуЇ основний стан частинки в неск≥нченно глибокому пр€мокутному €щику шириною l. ќбчислити ≥мов≥рн≥сть знаходженн€ частинки в малому ≥нтервал≥  l = 0,01 l у двох випадках: 1) поблизу ст≥нки (
l = 0,01 l у двох випадках: 1) поблизу ст≥нки ( ); 2) у середн≥й частин≥ €щика
); 2) у середн≥й частин≥ €щика  .
.
ƒано:
 l = 0,01 l
l = 0,01 l
__________
W1 Ц?
W2 Ц?
–озвТ€зуванн€. ≤мов≥рн≥сть того, що частинка буде ви€влена в ≥нтервал≥ dx (в≥д х до х+dх), пропорц≥йна цьому ≥нтервалу й квадрату модул€ хвильовоњ функц≥њ, €ка описуЇ даний стан
dW = 
” першому випадку шукана ≥мов≥рн≥сть знаходитьс€ ≥нтегруванн€м у межах в≥д 0 до 0,01l
W =  (1)
(1)
«нак модул€ пропущений, тому що  - функц≥€ в цьому випадку не Ї комплексною.
- функц≥€ в цьому випадку не Ї комплексною.
ќск≥льки х зм≥нюЇтьс€ в ≥нтервал≥ (0  0,01 l) ≥, отже,
0,01 l) ≥, отже,  <<1, справедлива наближена р≥вн≥сть
<<1, справедлива наближена р≥вн≥сть
 .
.
« урахуванн€м цього вираз (1) набуде вигл€ду
W =  .
.
ѕ≥сл€ ≥нтегруванн€ одержимо
W =  .
.
” другому випадку можна об≥йтис€ без ≥нтегруванн€, оск≥льки квадрат модул€ хвильовоњ функц≥њ поблизу њњ максимуму в заданому малому ≥нтервал≥ ( l = 0,01l) практично не зм≥нюЇтьс€. Ўукана ≥мов≥рн≥сть у другому випадку визначаЇтьс€ виразом
l = 0,01l) практично не зм≥нюЇтьс€. Ўукана ≥мов≥рн≥сть у другому випадку визначаЇтьс€ виразом
W = 
або
W =  .
.
«адач≥
623. «найти: а) рад≥уси трьох перших бор≥вських електронних р≥вн≥в в атом≥ водню; б) швидк≥сть електрона на цих р≥вн€х.
¬≥дпов≥дь:  = 53 пм;
= 53 пм;  = 212 пм;
= 212 пм;  = 477 пм;
= 477 пм;  = 2,19 ћм/c;
= 2,19 ћм/c;  = 1,1 ћм/c;
= 1,1 ћм/c;  = 0,73 ћм/c.
= 0,73 ћм/c.
624. «найти числове значенн€ к≥нетичноњ, потенц≥альноњ ≥ повноњ енерг≥й електрона на першому бор≥вському енергетичному р≥вн≥.
¬≥дпов≥дь:  = 13,6 е¬; U = -27,2 е¬; E = -13,6 е¬.
= 13,6 е¬; U = -27,2 е¬; E = -13,6 е¬.
625. ќбчислити к≥нетичну енерг≥ю електрона, €кий перебуваЇ на n -му енергетичному р≥вн≥ атома водню. «адачу розвТ€зати дл€ n = 1, 2, 3 ≥ ∞.
¬≥дпов≥дь:  ;
; 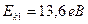 ;
;  ;
;  ;
;  .
.
626. «найти: а) пер≥од обертанн€ електрона на першому бор≥вському енергетичному р≥вн≥ в атом≥ водню; б) кутову швидк≥сть обертанн€ електрона.
¬≥дпов≥дь:  = 1,52.10
= 1,52.10  с; ω = 4,13.10
с; ω = 4,13.10  рад/c.
рад/c.
627. «найти: а) рад≥ус першого бор≥вського енергетичного р≥вн€ дл€ одноразово ≥он≥зованого атома гел≥ю; б) швидк≥сть електрона на цьому р≥вн≥.
¬≥дпов≥дь:  = 26,6 пм;
= 26,6 пм;  = 4,38 ћм/c.
= 4,38 ћм/c.
628. —користавшись постулатами теор≥њ Ѕора, обчислити: а) рад≥уси двох перших енергетичних р≥вн≥в в атом≥ водню; б) швидкост≥ електрона на цих р≥вн€х.
¬≥дпов≥дь:  = 53 пм;
= 53 пм;  = 212 пм;
= 212 пм;  = 2,19 ћм/c;
= 2,19 ћм/c;  = 1,1 ћм/c.
= 1,1 ћм/c.
629. Ќа €кому енергетичному р≥вн≥ в атом≥ водню швидк≥сть електрона дор≥внюЇ 734 км/с?
¬≥дпов≥дь: n = 3.
630. ¬изначити кутову швидк≥сть електрона на першому бор≥вському енергетичному р≥вн≥ в атом≥ водню.
¬≥дпов≥дь: ω = 4,13 10  с
с  .
.
631. –озрахувати значенн€ кулон≥вськоњ сили прит€ганн€ ≥ напружен≥сть електричного пол€ €дра на першому й другому енергетичних р≥вн€х в атом≥ водню.
|
|
|
¬≥дпов≥дь:  = 82,4 нЌ;
= 82,4 нЌ;  = 512 √¬/м;
= 512 √¬/м;  = 5,14 нЌ;
= 5,14 нЌ;  = 32,1 √¬/м.
= 32,1 √¬/м.
632. јтом водню переводитьс€ з нормального стану в збуджений, що характеризуЇтьс€ головним квантовим числом 2. –озрахувати енерг≥ю збудженн€ цього атома.
¬≥дпов≥дь:  E = 10,2 е¬.
E = 10,2 е¬.
633. јтом водню перебуваЇ в основному стан≥. ” ск≥льки раз≥в зб≥льшитьс€ рад≥ус енергетичного р≥вн€ електрона в атом≥, €кщо в≥н поглине квант з енерг≥Їю 12,09 е¬?
¬≥дпов≥дь:  /
/  = 9.
= 9.
634. ѕерех≥д електрона в атом≥ водню з n -го на k -й енергетичний р≥вень (k = 1) супроводжуЇтьс€ випром≥нюванн€м фотона з довжиною хвил≥ 102,6 нм. «найти рад≥ус n -го енергетичного р≥вн€.
¬≥дпов≥дь: r = 475 пм.
635. ѕоказати, що дл€ атома водню на бор≥вських стац≥онарних енергетичних р≥вн€х укладаЇтьс€ ц≥ле число довжин хвиль де Ѕройл€. ¬изначити довжини хвиль де Ѕройл€ на першому ≥ третьому енергетичних р≥вн€х.
¬≥дпов≥дь:  = n λ;
= n λ;  = 332 пм;
= 332 пм;  = 996 пм.
= 996 пм.
636. яку роботу необх≥дно виконати, щоб перевести електрон з другого енергетичного р≥вн€ атома водню за меж≥ його прит€ганн€ €дром?
¬≥дпов≥дь: A = 5,45.10-19 ƒж.
637. —користавшись постулатами Ѕора, визначити дл€ електрона, що перебуваЇ на першому й другому енергетичних р≥вн€х в атом≥ водню, в≥дношенн€ рад≥ус≥в цих р≥вн≥в.
¬≥дпов≥дь:  /
/  = 4.
= 4.
638. —користавшись постулатами Ѕора, визначити дл€ електрона, що перебуваЇ на першому й другому енергетичних р≥вн€х в атом≥ водню, в≥дношенн€ магн≥тного моменту електрона до його механ≥чного моменту.
¬≥дпов≥дь:  л / кг.
л / кг.
639. —користавшись постулатами Ѕора, визначити дл€ електрона, що перебуваЇ на першому й другому енергетичних р≥вн€х в атом≥ водню, в≥дношенн€ њх повних енерг≥й.
¬≥дпов≥дь:  .
.
640. ¬изначити, €к зм≥нитьс€ орб≥тальний момент ≥мпульсу електрона в атом≥ водню при його переход≥ ≥з збудженого стану в основний стан, €кщо при цьому випром≥нюЇтьс€ один квант енерг≥њ з довжиною хвил≥ λ = 97,25 нм.
¬≥дпов≥дь: «меншитьс€ у 4 рази.
641. ” спектр≥ атомарного водню ≥нтервал м≥ж першими двома спектральними л≥н≥€ми, €к≥ належать до сер≥њ Ѕальмера, складаЇ λ = 6 ,54.10  м. ¬изначити сталу –≥дберга.
м. ¬изначити сталу –≥дберга.
¬≥дпов≥дь: R = 1,09 10 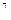 м
м  .
.
642. вант св≥тла з енерг≥Їю ≈ = 15 е¬ вибиваЇ електрон з атома водню, що перебуваЇ в нормальному стан≥. « €кою в≥дносною швидк≥стю буде рухатис€ цей електрон далеко в≥д €дра?
¬≥дпов≥дь: υ = 7,01.10  м/c.
м/c.
643. ќбчислити цикл≥чну частоту обертанн€ електрона на другому бор≥вському енергетичному р≥вн≥ ≥она Ќе  .
.
¬≥дпов≥дь: ω = 2,07.10  c
c  .
.
644. «найти дл€ воднепод≥бних систем магн≥тний момент, що в≥дпов≥даЇ руху електрона на n -му енергетичному р≥вн≥, а також в≥дношенн€ магн≥тного моменту до механ≥чного.
¬≥дпов≥дь: 

645. ќбчислити ≥ндукц≥ю магн≥тного пол€ в центр≥ атома водню, обумовленого рухом електрона по першому бор≥вському енергетичному р≥вн≥.
¬≥дпов≥дь: B = 12,5 “л.
646. ≈нерг≥€ зв'€зку електрона в основному стан≥ атома Ќе дор≥внюЇ  = 24,6 е¬. «найти енерг≥ю, необх≥дну дл€ видаленн€ обох електрон≥в з цього атома.
= 24,6 е¬. «найти енерг≥ю, необх≥дну дл€ видаленн€ обох електрон≥в з цього атома.
¬≥дпов≥дь: 
647. ќбчислити за теор≥Їю Ѕора пер≥од  обертанн€ електрона в атом≥ водню, що перебуваЇ в збудженому стан≥ з головним квантовим числом n = 2.
обертанн€ електрона в атом≥ водню, що перебуваЇ в збудженому стан≥ з головним квантовим числом n = 2.
¬≥дпов≥дь:  = 1,22.10
= 1,22.10  с.
с.
648. ” ск≥льки раз≥в зм≥нитьс€ пер≥од  обертанн€ електрона в атом≥ водню, €кщо при переход≥ в незбуджений стан атом випром≥нюЇ фотон з довжиною хвил≥ λ = 97,5 нм?
обертанн€ електрона в атом≥ водню, €кщо при переход≥ в незбуджений стан атом випром≥нюЇ фотон з довжиною хвил≥ λ = 97,5 нм?
¬≥дпов≥дь:  .
.
649. Ќа ск≥льки зм≥нилас€ к≥нетична енерг≥€ електрона в атом≥ водню при випром≥нюванн≥ ним фотона з довжиною хвил≥ λ = 435нм?
¬≥дпов≥дь:  .
.
650. «найти найб≥льшу довжину хвил≥ у видим≥й област≥ спектра атома водню.
¬≥дпов≥дь: λ = 656 нм.
651. «найти найб≥льшу довжину хвил≥ в ультраф≥олетов≥й сер≥њ Ћаймана спектра атома водню. яку найменшу швидк≥сть повинн≥ мати електрони, щоб п≥д час збудженн€ атом≥в водню ударами електрон≥в зС€вилас€ ц€ л≥н≥€?
|
|
|
¬≥дпов≥дь: λ = 121 нм; υ = 1,9 ћм/с.
652. ¬изначити потенц≥ал ≥он≥зац≥њ атома водню.
¬≥дпов≥дь:  = 13,6 ¬.
= 13,6 ¬.
653. ¬изначити перший потенц≥ал збудженн€ атома водню.
¬≥дпов≥дь:  = 10,2 ¬.
= 10,2 ¬.
654. яку найменшу енерг≥ю (в електрон-вольтах) повинн≥ мати електрони, щоб при збудженн≥ атом≥в водню ударами цих електрон≥в по€вилис€ вс≥ л≥н≥њ вс≥х сер≥й спектра водню? яку найменшу швидк≥сть повинн≥ мати ц≥ електрони?
¬≥дпов≥дь: E = 13,6 е¬; υ = 2,2 ћм/с.
655. ” €ких межах повинна зм≥нюватись енерг≥€ електрон≥в, щоб при збудженн≥ ними атом≥в водню, €к≥ перебувають у нормальному стан≥, енергетичний спектр випром≥нюванн€ мав т≥льки одну спектральну л≥н≥ю?
¬≥дпов≥дь: 10,2 е¬ ≤ ≈ ≤ 12,1 е¬.
656. яку найменшу енерг≥ю (в електрон-вольтах) повинн≥ мати електрони, щоб при збудженн≥ ними атом≥в водню, спектр водню мав три спектральн≥ л≥н≥њ? «найти довжини хвиль цих л≥н≥й.
¬≥дпов≥дь: E ≥ 12,04 е¬;  = 656 нм;
= 656 нм;  = 122 нм;
= 122 нм;  = 103 нм.
= 103 нм.
657. ” €ких межах повинн≥ розм≥щуватись довжини хвиль монохроматичного св≥тла, щоб при збудженн≥ атом≥в водню квантами цього св≥тла спостер≥галис€ три спектральн≥ л≥н≥њ?
¬≥дпов≥дь: 97,3 нм ≤ λ ≤ 102,6 нм.
658. Ќа ск≥льки зм≥нитьс€ к≥нетична енерг≥€ електрона в атом≥ водню при випром≥нюванн≥ ним фотона з довжиною хвил≥ λ = 486 нм?
¬≥дпов≥дь: Δ E  = 2,56 е¬.
= 2,56 е¬.
659. ” €ких межах повинн≥ лежати довжини хвиль монохроматичного св≥тла, щоб при збудженн≥ атом≥в водню квантами цього св≥тла рад≥ус енергетичного р≥вн€ електрона зб≥льшивс€ в 9 раз≥в?
¬≥дпов≥дь: 97,3 нм ≤ λ ≤ 102,6 нм.
660. Ќа дифракц≥йну гратку нормально падаЇ пучок св≥тла в≥д розр€дноњ трубки, наповненоњ атомарним воднем. —тала гратки дор≥внюЇ 5.10-4 см. якому переходу електрона в≥дпов≥даЇ спектральна л≥н≥€, що спостер≥гаЇтьс€ за допомогою ц≥Їњ гратки у спектр≥ п'€того пор€дку п≥д кутом 41∞?
¬≥дпов≥дь: 3 →2.
661. «найти найменшу довжину хвил≥ фотона, що випром≥нюЇтьс€ електроном при переход≥ ≥з збудженого в основний стан в ≥он≥ гел≥ю  .
.
¬≥дпов≥дь: λ = 30,4 нм.
662. яка найменша енерг≥€ необх≥дна дл€ збудженн€ ≥она 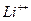 ?
?
¬≥дпов≥дь: E = 92 е¬.
663. «найти р≥зницю енерг≥й ≥он≥зац≥њ ≥он≥в  та атома водню.
та атома водню.
¬≥дпов≥дь: Δ E = 41 е¬.
664. ¬изначити межу сер≥њ водневих л≥н≥й, розм≥щених в далек≥й ультраф≥олетов≥й частин≥ спектра (сер≥€ Ћаймана).
¬≥дпов≥дь: λ = (121,6 Ц91,2) нм.
665. ¬изначити енерг≥ю фотона, що в≥дпов≥даЇ найменш≥й довжин≥ хвил≥ в ультраф≥олетов≥й сер≥њ водню.
¬≥дпов≥дь: E = 2,18.10  ƒж.
ƒж.
666. «найти довжини хвиль першоњ, другоњ ≥ третьоњ л≥н≥й видимоњ сер≥њ водню (сер≥€ Ѕальмера).
¬≥дпов≥дь:  = 656,3 нм;
= 656,3 нм;  = 486,1 нм;
= 486,1 нм;  = 434 нм.
= 434 нм.
667. „ому дор≥внюЇ довжина хвил≥ четвертоњ спектральноњ л≥н≥њ в ≥нфрачервон≥й област≥ спектра водню (сер≥€ ѕашена)?
¬≥дпов≥дь:  = 1,005 мкм.
= 1,005 мкм.
668. ≈кспериментально встановлено, що друга спектральна л≥н≥€ водневоњ сер≥њ Ѕрекета в≥дпов≥даЇ довжин≥ хвил≥ 2,63 мкм. Ќа п≥дстав≥ цих даних установити наближене значенн€ сталоњ –≥дберга.
¬≥дпов≥дь: R = 1,095.10 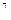 м
м  .
.
669. Ќайб≥льша довжина хвил≥ спектральноњ водневоњ л≥н≥њ сер≥њ Ћаймана 121,6 нм. ќбчислити найб≥льшу довжину хвил≥ в сер≥њ Ѕальмера.
¬≥дпов≥дь: λ = 656,6 нм.
670. ѕри переход≥ електрона атома водню з одного з можливих енергетичних р≥вн≥в на ≥нший, б≥льш близький до €дра, енерг≥€ атома зменшуЇтьс€ на 1,892 е¬. ¬изначити довжину хвил≥ випром≥нюванн€.
|
|
|
¬≥дпов≥дь: λ = 657 нм.
671. ќбчислити найменше значенн€ енерг≥њ, при €кому в результат≥ збудженн€ атом≥в водню з'€вл€Їтьс€ повний спектр.
¬≥дпов≥дь: E = 13,63 е¬.
672. јтомарний водень переведений з нормального стану в збуджений з головним квантовим числом n = 3. як≥ спектральн≥ л≥н≥њ можуть з'€витис€ в спектр≥ водню при переход≥ атома з≥ збудженого стану в нормальний?
¬≥дпов≥дь: 2→1, λ = 121,6 нм; 3→1, λ = 102,6 нм; 3→2, λ = 656,3 нм.
673. як≥ спектральн≥ л≥н≥њ з'€вл€тьс€ у видим≥й област≥ спектра при збудженн≥ атом≥в водню електронами з енерг≥Їю 13 е¬?
¬≥дпов≥дь:  = 656,3 нм;
= 656,3 нм;  = 486,1 нм;
= 486,1 нм;  = 434,0 нм.
= 434,0 нм.
674. јтоми водню осв≥тлюЇтьс€ ультраф≥олетовим випром≥нюванн€м з довжиною хвил≥ 100 нм. ¬изначити, €к≥ спектральн≥ л≥н≥њ з'€вл€тьс€ в спектр≥ водню.
¬≥дпов≥дь:  = 121,6 нм;
= 121,6 нм;  = 102,6 нм;
= 102,6 нм;  = 656,6 нм.
= 656,6 нм.
675. –≥зниц€ довжини хвиль м≥ж головними л≥н≥€ми сер≥й Ћаймана ≥ Ѕальмера в спектр≥ атомарного водню дор≥внюЇ λ = 534,7 нм. ¬изначити за цими даними сталу ѕланка.
¬≥дпов≥дь: h = 6,64 .10  ƒж с.
ƒж с.
676. ≈лектрон, що перебуваЇ далеко в≥д €дра атома водню ≥ маЇ швидк≥сть υ = 1,870.10  м/с, захоплюЇтьс€ цим €дром, у результат≥ чого утворюЇтьс€ збуджений атом водню. ¬изначити довжину хвил≥ фотона, що випром≥нюЇтьс€ при переход≥ атома в нормальний стан.
м/с, захоплюЇтьс€ цим €дром, у результат≥ чого утворюЇтьс€ збуджений атом водню. ¬изначити довжину хвил≥ фотона, що випром≥нюЇтьс€ при переход≥ атома в нормальний стан.
¬≥дпов≥дь: λ = 121 нм.
677. як≥ спектральн≥ л≥н≥њ з'€вл€тьс€ при збудженн≥ атомарного водню електронами з енерг≥Їю: а) 12,5 е¬; б) 14 е¬?
¬≥дпов≥дь: а)  = 103 нм;
= 103 нм;  = 127 нм;
= 127 нм;  = 656 нм; б) вс≥.
= 656 нм; б) вс≥.
678. ѕри спостереженн≥ спектра атомарного водню, отриманого за допомогою дифракц≥йноњ гратки з пер≥одом d = 2 мкм, ви€влено, що одна з≥ спектральних л≥н≥й сер≥њ Ѕальмера в спектр≥ другого пор€дку в≥дпов≥даЇ куту дифракц≥њ 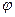 = 29∞05''. ¬изначити головне квантове число енергетичного р≥вн€ атома, переходу з €кого в≥дпов≥даЇ дана л≥н≥€.
= 29∞05''. ¬изначити головне квантове число енергетичного р≥вн€ атома, переходу з €кого в≥дпов≥даЇ дана л≥н≥€.
¬≥дпов≥дь: n = 4.
679. —користавшись постулатами Ѕора, визначити дл€ дворазово ≥он≥зованого атома л≥т≥ю (Li  ) рад≥ус першого енергетичного р≥вн€.
) рад≥ус першого енергетичного р≥вн€.
¬≥дпов≥дь:  = 18 пм.
= 18 пм.
680. ¬изначити довжини хвиль де Ѕройл€ електрона й протона, €к≥ пройшли однакову прискорювальну р≥зницю потенц≥ал≥в U = 400 ¬.
¬≥дпов≥дь: 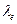 = 61,4 пм;
= 61,4 пм; 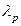 =1,43 пм.
=1,43 пм.
681. ≈лектрон, початковою швидк≥стю €кого можна знехтувати, пройшов прискорювану р≥зницю потенц≥ал≥в U. «найти довжину хвил≥ де Ѕройл€ дл€ двох випадк≥в: а) U = 51 B, б) U = 510 к¬.
¬≥дпов≥дь: λ1 =172 пм; λ2 = 1,4 пм.
682. яку прискорювану р≥зницю потенц≥ал≥в маЇ пройти електрон, щоб довжина хвил≥ де Ѕройл€ дор≥внювала 10-8 м?
¬≥дпов≥дь: U1 = 0,015 ¬.
683. ѕор≥вн€ти довжину хвил≥ де Ѕройл€ дл€ електрона ≥ частинки масою 0,1 г, €к≥ рухаютьс€ з однаковими швидкост€ми. який висновок можна зробити?
¬≥дпов≥дь: λе/λч = 1,09.1026 раз≥в.
684. ¬изначити довжину хвил≥ де Ѕройл€ дл€ протона, що рухаЇтьс€ з≥ швидк≥стю  = 0,6 с (с Ц швидк≥сть св≥тла у вакуум≥).
= 0,6 с (с Ц швидк≥сть св≥тла у вакуум≥).
¬≥дпов≥дь: λ = 1,76.10-15 м.
685. ≈лектрон рухаЇтьс€ вздовж коловоњ траЇктор≥њ рад≥усом 0,5 см в однор≥дному магнетному пол≥ з ≥ндукц≥Їю 8 м“л. ¬изначити довжину хвил≥ де Ѕройл€ електрона.
¬≥дпов≥дь: λ = 1,035.10 -10 м.
686. ¬изначити довжину хвил≥ де Ѕройл€ електрона, €кщо його к≥нетична енерг≥€ дор≥внюЇ 1 е¬.
¬≥дпов≥дь: λ = 10-9 м.
687. ¬изначити довжину хвил≥ де Ѕройл€ ≥ к≥нетичну енерг≥ю протона, €кий рухаЇтьс€ з≥ швидк≥стю  = 0,99 с (с Ц швидк≥сть св≥тла у вакуум≥).
= 0,99 с (с Ц швидк≥сть св≥тла у вакуум≥).
¬≥дпов≥дь: λ = 188.10-16 м; “= 9,15.10-10 ƒж.
688. ѕор≥вн€ти довжини хвиль де Ѕройл€ електрона й ≥она He+, €к≥ пройшли однакову р≥зницю потенц≥ал≥в U = 1 к¬.
¬≥дпов≥дь: λе = 3,88.10-11 м; λп = 4,53.10-13 м.
689. « €кою швидк≥стю рухаЇтьс€ електрон, €кщо довжина хвил≥ де Ѕройл€ електрона дор≥внюЇ 2,456 нм?
¬≥дпов≥дь: υ =2,96.105м/с.
690. «найд≥ть довжину хвил≥ де Ѕройл€ дл€ протона, €кий пройшов прискорюючи р≥зницю потенц≥ал≥в: 1) 1 к¬, 2) 1 ћ¬.
¬≥дпов≥дь: λ1 = 9,06.10-13 м; λ2 = 2,87.10-14 м.
691. ≥нетична енерг≥€ протона дор≥внюЇ його енерг≥њ спокою. ќбчислити довжину хвил≥ де Ѕройл€ цього протона.
¬≥дпов≥дь: 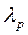 =7,64.10-16 м.
=7,64.10-16 м.
692. ¬изначити к≥нетичн≥ енерг≥њ протона ≥ електрона, дл€ €ких довжина хвил≥ де Ѕройл€ дор≥внюЇ 0,06 нм.
¬≥дпов≥дь:  = 419 е¬;
= 419 е¬; 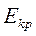 = 0,228 е¬.
= 0,228 е¬.
693. ѕротон маЇ к≥нетичну енерг≥ю, що дор≥внюЇ його енерг≥њ спокою. ” ск≥льки раз≥в зм≥нитьс€ довжина хвил≥ де Ѕройл€ протона, €кщо його к≥нетична енерг≥€ зб≥льшитьс€ у 2 рази?
¬≥дпов≥дь:  /
/  = 1,63.
= 1,63.
|
|
|
694. ≥нетична енерг≥€ електрона дор≥внюЇ його енерг≥њ спокою. ќбчислити довжину хвил≥ де Ѕройл€ дл€ такого електрона.
¬≥дпов≥дь:  = 1,4 пм.
= 1,4 пм.
695. ¬икористовуючи постулати Ѕора, знайти зв'€зок м≥ж довжиною хвил≥ де Ѕройл€ ≥ довжиною колового енергетичного р≥вн€.
¬≥дпов≥дь:  .
.
696. яку к≥нетичну енерг≥ю повинен мати електрон, щоб його довжина хвил≥ де Ѕройл€ дор≥внювала комптон≥вськ≥й довжин≥ хвил≥?
¬≥дпов≥дь:  = 0,25 ће¬.
= 0,25 ће¬.
697. який ≥мпульс повинен мати протон, щоб його хвил€ де Ѕройл€ дор≥внювала комптон≥вськ≥й довжин≥ хвил≥?
¬≥дпов≥дь: p = 5⋅10  кг⋅м/c.
кг⋅м/c.
698. «найти довжину хвил≥ де Ѕройл€ дл€ електрона, що перебуваЇ в рус≥ на першому бор≥вському енергетичному р≥вн≥ в атом≥ водню.
¬≥дпов≥дь:  = 0,33 нм.
= 0,33 нм.
699. Ќаписати вираз дл€ хвил≥ де Ѕройл€ λ рел€тив≥стськоњ частинки маси m; а) через њњ швидк≥сть υ; б) через к≥нетичну енерг≥ю  .
.
¬≥дпов≥дь: 

700. ѕри €кому значенн≥ швидкост≥ υ довжина хвил≥ де Ѕройл€ м≥крочастинки дор≥внюЇ њњ комптон≥вськ≥й довжин≥ хвил≥?
¬≥дпов≥дь: υ = 0,71 с.
701. ѕри €к≥й швидкост≥ υ електрона його довжина хвил≥ де Ѕройл€ буде дор≥внювати 500 нм?
¬≥дпов≥дь:  =1,46 км/с.
=1,46 км/с.
702. «найти довжину хвил≥ де Ѕройл€ електрона, що рухаЇтьс€ з≥ швидк≥стю 20 км/с. ƒо €коњ област≥ електромагнетного спектра можна в≥днести довжину хвил≥, €ка дор≥внюЇ знайден≥й?
¬≥дпов≥дь:  = 36,4 нм.
= 36,4 нм.
703. Ўвидкост≥ теплових нейтрон≥в €дерних реактор≥в близьк≥ до 2,5 км/с. «найти довжину хвил≥ де Ѕройл€ дл€ таких нейтрон≥в.
¬≥дпов≥дь:  = 159 пм.
= 159 пм.
704. ” телев≥з≥йн≥й трубц≥ проекц≥йного типу електрони розган€ютьс€ до швидкост≥ 108 м/с. ¬изначити довжину хвил≥ де Ѕройл€ електрон≥в без урахуванн€ залежност≥ маси в≥д швидкост≥.
¬≥дпов≥дь:  = 7,27 пм.
= 7,27 пм.
705. «найти довжину хвил≥ де Ѕройл€ дл€ електрона, що рухаЇтьс€ з≥ швидк≥стю, €ка дор≥внюЇ 0,8 швидкост≥ св≥тла. ¬рахувати зм≥ну маси з≥ швидк≥стю.
¬≥дпов≥дь:  = 1,82 пм.
= 1,82 пм.
706. ќбчислити довжину хвил≥ де Ѕройл€ дл€ протона з к≥нетичною енерг≥Їю 100 е¬.
¬≥дпов≥дь:  = 2,86 пм.
= 2,86 пм.
707. «найти довжину хвил≥ де Ѕройл€ дл€ α-частинки, нейтрона ≥ молекули азоту, що рухаютьс€ ≥з середньою квадратичною швидк≥стю при температур≥ 25∞ —.
¬≥дпов≥дь:  = 73 пм;
= 73 пм;  = 145 пм;
= 145 пм;  = 28 пм.
= 28 пм.
708. ≈лектрон рухаЇтьс€ на другому енергетичному р≥вн≥ атома водню. «найти його довжину хвил≥ де Ѕройл€.
¬≥дпов≥дь:  = 0,665 нм.
= 0,665 нм.
709. ≈лектрон маЇ к≥нетичну енерг≥ю 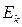 = 1,02 ће¬. ” ск≥льки раз≥в зм≥нитьс€ довжина хвил≥ де Ѕройл€, €кщо к≥нетична енерг≥€ електрон≥в зменшитьс€ удв≥ч≥.
= 1,02 ће¬. ” ск≥льки раз≥в зм≥нитьс€ довжина хвил≥ де Ѕройл€, €кщо к≥нетична енерг≥€ електрон≥в зменшитьс€ удв≥ч≥.
¬≥дпов≥дь: 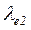 /
/  = 1,63.
= 1,63.
710. —ередн€ к≥нетична енерг≥€ електрона в основному стан≥ атома водню дор≥внюЇ 13,6е¬. ¬икористовуючи сп≥вв≥дношенн€ невизначеностей, знайти найменшу похибку, з €кою можна обчислити координату електрона в атом≥.
¬≥дпов≥дь: Δ x = 52,8 пм.
711. ѕоказати, що дл€ частинки, невизначен≥сть координати €коњ складаЇ Δ х = λ /(2 π ) (λ Ц довжина хвил≥ де Ѕройл€), невизначен≥сть њњ швидкост≥ за величиною дор≥внюЇ сам≥й швидкост≥ частинки.
712. ¬иход€чи з≥ сп≥вв≥дношенн€ невизначеностей, оц≥нити розм≥ри €дра атома, вважаючи, що м≥н≥мальна енерг≥€ нуклона в €др≥ 8 ће¬.
¬≥дпов≥дь: d = 1,6 фм.
713. ¬икористовуючи сп≥вв≥дношенн€ невизначеностей, оц≥нити енерг≥ю електрона, що перебуваЇ на першому бор≥вському енергетичному р≥вн≥ в атом≥ водню.
¬≥дпов≥дь: E = 13,6 е¬.
714. ≈лектрон перебуваЇ в одновим≥рн≥й потенц≥альн≥й €м≥ з неск≥нченно високими ст≥нками, ширина €коњ 1,4 10  м. ¬изначити енерг≥ю, що випром≥нюЇтьс€ при переход≥ електрона з третього енергетичного р≥вн€ на другий.
м. ¬изначити енерг≥ю, що випром≥нюЇтьс€ при переход≥ електрона з третього енергетичного р≥вн€ на другий.
¬≥дпов≥дь: E = 1,52 .10  ƒж = 0,95 е¬.
ƒж = 0,95 е¬.
715. ≈лектрон знаходитьс€ в одновим≥рн≥й потенц≥альн≥й €м≥ з неск≥нченно високими ст≥нками, ширина €коњ l = 1 нм. ¬изначити найменшу р≥зницю енергетичних р≥вн≥в електрона.
¬≥дпов≥дь: Δ E = 1,78 .10  ƒж = 1,11 е¬.
ƒж = 1,11 е¬.
716. „астинка в потенц≥альн≥й €м≥ шириною l перебуваЇ у збудженому стан≥. ¬изначити ≥мов≥рн≥сть перебуванн€ частинки в ≥нтервал≥ 0 < x < 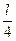 на другому енергетичному р≥вн≥.
на другому енергетичному р≥вн≥.
¬≥дпов≥дь: W =  .
.
717. ¬изначити ширину одновим≥рноњ потенц≥альноњ €ми з неск≥нченно високими ст≥нками, €кщо при переход≥ електрона з третього енергетичного р≥вн€ на другий випром≥нюЇтьс€ енерг≥€ 1 е¬?
¬≥дпов≥дь: l = 1,37 нм.
718. «найти хвильову функц≥ю ≥ значенн€ енерг≥њ частинки масою m, що перебуваЇ в одновим≥рн≥й неск≥нченно глибок≥й потенц≥альн≥й €м≥ шириною l.
¬≥дпов≥дь:  .
.
719. јльфа-частинка знаходитьс€ у неск≥нченно глибок≥й одновим≥рн≥й потенц≥альн≥й €м≥. „ому дор≥внюЇ ширина €ми, €кщо м≥н≥мальна енерг≥€ частинки складаЇ 6 ће¬?
¬≥дпов≥дь: l = 2,9.10-15 м.
720. ≈лектрон знаходитьс€ у неск≥нченно глибок≥й одновим≥рн≥й потенц≥альн≥й €м≥ шириною 0,1 нм. ќбчислити довжину хвил≥ випром≥нюванн€ при переход≥ електрона з другого на перший енергетичний р≥вень.
¬≥дпов≥дь: λ = 11 нм.
721. ѕротон знаходитьс€ в неск≥нченно глибок≥й одновим≥рн≥й потенц≥альн≥й €м≥ шириною 0,01 пм. ќбчислити довжину хвил≥ випром≥нюванн€ при переход≥ протона з третього на другий енергетичний р≥вень.
¬≥дпов≥дь: λ = 1,22.10-13 м.
722. јтом водню знаходитьс€ у неск≥нченно глибок≥й одновим≥рн≥й потенц≥альн≥й €м≥ шириною 0,1 нм. ќбчислити р≥зницю енерг≥й сус≥дн≥х р≥вн≥в, €к≥ в≥дпов≥дають середн≥й енерг≥њ теплового руху атома при температур≥ 625 .
¬≥дпов≥дь: 
 ; n = 2;
; n = 2; 
723. „астинка знаходитьс€ у неск≥нченно глибок≥й одновим≥рн≥й потенц≥альн≥й €м≥ шириною l в основному стан≥. ” €ких точках €ми густина ≥мов≥рност≥ ви€вленн€ частинки зб≥гаЇтьс€ з класичною густиною ≥мов≥рност≥.
¬≥дпов≥дь: ωкл .=  ω =
ω = 

724. „астинка знаходитьс€ у неск≥нченно глибок≥й одновим≥рн≥й потенц≥альн≥й €м≥ шириною l в основному стан≥. „ому дор≥внюЇ в≥дношенн€ густин ≥мов≥рност≥ ви€вленн€ частинки в центр≥ €ми до класичноњ густини ≥мов≥рност≥.
¬≥дпов≥дь: ωк л.=  ω =
ω =  x =
x = 

725. „астинка знаходитьс€ у неск≥нченно глибок≥й одновим≥рн≥й потенц≥альн≥й €м≥ шириною l на першому збудженому р≥вн≥. ” €ких точках €ми густина ≥мов≥рност≥ ви€вленн€ частинки максимальна?
¬≥дпов≥дь: ω =  n=2;
n=2; 
726. „астинка знаходитьс€ у неск≥нченно глибок≥й одновим≥рн≥й потенц≥альн≥й €м≥ шириною l на другому енергетичному р≥вн≥. ¬изначити ≥мов≥рн≥сть ви€вленн€ частинки в межах в≥д 0 до l / 3.
¬≥дпов≥дь: W=0,40.
727. „астинка знаходитьс€ у неск≥нченно глибок≥й одновим≥рн≥й потенц≥йн≥й €м≥ шириною l в основному стан≥. «найти в≥дношенн€ ≥мов≥рност≥ перебуванн€ частинки в межах в≥д 0 до l /3 ≥ в≥д l /3 до 2 l /3.
¬≥дпов≥дь: 
728. „астинка знаходитьс€ у неск≥нченно глибок≥й одновим≥рн≥й потенц≥альн≥й €м≥ шириною l. ќбчислити в≥дношенн€ ≥мов≥рност≥ перебуванн€ частинки в межах в≥д 0 до l / 4 дл€ першого ≥ другого енергетичних р≥вн≥в.
¬≥дпов≥дь: 
729. „астинка перебуваЇ в основному стан≥ в одновим≥рн≥й пр€мокутн≥й потенц≥альн≥й €м≥ шириною l з абсолютно непроникними ст≥нками (0< x < l). «найти ймов≥рн≥сть перебуванн€ частинки в област≥ 
¬≥дпов≥дь:  .
.
730. ≈лектрон перебуваЇ в пр€мокутн≥й потенц≥альн≥й €м≥ з непроникними ст≥нками. Ўирина €ми l = 0,2 нм, енерг≥€ електрона в €м≥ E = 37,8 е¬. ¬изначити номер n енергетичного р≥вн€.
¬≥дпов≥дь: n = 2.
731. „астинка перебуваЇ в потенц≥альн≥й €м≥ в основному стан≥. яка ≥мов≥рн≥сть ви€вленн€ частинки: а) у середн≥й третин≥ €ми; б) у крайн≥й третин≥ €ми?
¬≥дпов≥дь:  = 0,609;
= 0,609;  = 0,195.
= 0,195.
732. „астинка перебуваЇ у неск≥нченно глибок≥й, одновим≥рн≥й, пр€мокутн≥й потенц≥альн≥й €м≥. «найти в≥дношенн€ р≥зниц≥ енерг≥й  сус≥дн≥х енергетичних р≥вн≥в до енерг≥њ
сус≥дн≥х енергетичних р≥вн≥в до енерг≥њ  частинки у випадку, €кщо n = 2.
частинки у випадку, €кщо n = 2.
¬≥дпов≥дь: 
733. ≈лектрон перебуваЇ у неск≥нченно глибок≥й, одновим≥рн≥й, пр€мокутн≥й потенц≥альн≥й €м≥ шириною l = 0,1 нм. ¬изначити в електрон-вольтах найменшу р≥зницю енергетичних р≥вн≥в електрона.
¬≥дпов≥дь: Δ ≈ = 112 е¬.
734. „астинка в неск≥нченно глибок≥й, одновим≥рн≥й, пр€мокутн≥й потенц≥альн≥й €м≥ шириною l перебуваЇ у збудженому стан≥ (n = 3). ¬изначити, у €ких точках ≥нтервалу 0 < х < l густина ≥мов≥рност≥ перебуванн€ частинки маЇ максимальне ≥ м≥н≥мальне значенн€.
¬≥дпов≥дь: 
735. ” пр€мокутн≥й потенц≥альн≥й €м≥ шириною l з абсолютно непроникними ст≥нками (0 < х < l) перебуваЇ частинка в основному стан≥. «найти ≥мов≥рн≥сть W знаходженн€ ц≥Їњ частинки в област≥ l / 4 < x <  l.
l.
¬≥дпов≥дь: W = 0,82.
736. „астинка в неск≥нченно глибок≥й, одновим≥рн≥й, пр€мокутн≥й потенц≥альн≥й €м≥ перебуваЇ в основному стан≥. яка ймов≥рн≥сть W ви€вленн€ частинки в крайн≥й чверт≥ €ми?
¬≥дпов≥дь: W = 0,09.
737. „астинка перебуваЇ в основному стан≥ в пр€мокутн≥й €м≥ шириною l з абсолютно непроникними ст≥нками. ” ск≥льки раз≥в в≥др≥зн€ютьс€ ≥мов≥рност≥ ви€вити частинки: a) у крайн≥й третин≥ €ми; б) у крайн≥й чверт≥ €ми?
¬≥дпов≥дь:  /
/  = 2,17.
= 2,17.
738. ћоноенергетичний пот≥к електрон≥в (≈ = 100 е¬) падаЇ на низький пр€мокутний потенц≥альний барТЇр неск≥нченноњ ширини. ¬изначити висоту потенц≥ального барТЇра U, €кщо в≥домо, що 4% електрон≥в, що падають на барТЇр, в≥дбиваютьс€.
¬≥дпов≥дь: U = 55,6 е¬.
739. ≈лектрон з енерг≥Їю ≈ = 4,9 е¬ рухаЇтьс€ у позитивному напр€мку ос≥ x (рис.1). ¬исота U потенц≥ального барТЇра дор≥внюЇ 5 е¬. ѕри €к≥й ширин≥ d барТЇра ймов≥рн≥сть проходженн€ електрона кр≥зь нього буде дор≥внювати 0,2.
¬≥дпов≥дь: d = 0,495 нм.

–исунок 1
740. Ќаписати р≥вн€нн€ Ўред≥нгера дл€ електрона з енерг≥Їю ≈, що рухаЇтьс€ в позитивному напр€мку ос≥ x дл€ областей I та II (рис.1), €кщо на меж≥ цих областей ≥снуЇ низький потенц≥альний барТЇр висотою U.
¬≥дпов≥дь: 

 .
.
741. Ќа шл€ху електрона з довжиною хвил≥ де Ѕройл€  = 0,1 нм розм≥щений потенц≥альний барТЇр висотою U = 120 е¬. ¬изначити довжину хвил≥ де Ѕройл€
= 0,1 нм розм≥щений потенц≥альний барТЇр висотою U = 120 е¬. ¬изначити довжину хвил≥ де Ѕройл€  п≥сл€ проходженн€ барТЇра.
п≥сл€ проходженн€ барТЇра.
¬≥дпов≥дь:  .
.
742. ≈лектрон з енерг≥Їю ≈ = 100 е¬ попадаЇ на потенц≥альний бар'Їр висотою U = 64 е¬. ¬изначити ≥мов≥рн≥сть W того, що електрон в≥д≥б'Їтьс€ в≥д бар'Їра.
¬≥дпов≥дь: W = 0,0625.
743. ¬изначити показник заломленн€ n хвиль де Ѕройл€ при проходженн≥ частинкою потенц≥ального бар'Їра c коеф≥ц≥Їнтом в≥дбитт€ ρ = 0,5.
¬≥дпов≥дь: n = 0,172.
744. ѕри €кому в≥дношенн≥ висоти U потенц≥ального бар'Їра ≥ енерг≥њ ≈ електрона, що падаЇ на бар'Їр, коеф≥ц≥Їнт в≥дбитт€ ρ = 0,5?
¬≥дпов≥дь:  = 0,971.
= 0,971.
745. ≥нетична енерг≥€  електрона в два рази перевищуЇ висоту U потенц≥ального бар'Їра. ¬изначити коеф≥ц≥Їнт в≥дбитт€ ρ ≥ коеф≥ц≥Їнт проходженн€ τ електрон≥в на меж≥ бар'Їра.
електрона в два рази перевищуЇ висоту U потенц≥ального бар'Їра. ¬изначити коеф≥ц≥Їнт в≥дбитт€ ρ ≥ коеф≥ц≥Їнт проходженн€ τ електрон≥в на меж≥ бар'Їра.
¬≥дпов≥дь: ρ = 0,0295; τ = 0,97.
746. оеф≥ц≥Їнт проходженн€ протон≥в τ через потенц≥альний бар'Їр дор≥внюЇ 0,8. ¬изначити показник заломленн€  хвиль де Ѕройл€ на меж≥ бар'Їра.
хвиль де Ѕройл€ на меж≥ бар'Їра.
¬≥дпов≥дь:  = 0,384.
= 0,384.
747. ќбчислити коеф≥ц≥Їнт проходженн€ τ електрона з енерг≥Їю ≈ = 100 е¬ через потенц≥альний бар'Їр висотою U = 99,75 е¬.
¬≥дпов≥дь: τ = 0,2.
748. Ўирина d пр€мокутного потенц≥ального бар'Їра дор≥внюЇ 0,2 нм. –≥зниц€ енерг≥й U - ≈ = 1 е¬. ” ск≥льки раз≥в зм≥нитьс€ ≥мов≥рн≥сть W проходженн€ електрона через бар'Їр, €кщо р≥зниц€ енерг≥й зросте в n = 10 раз≥в?
¬≥дпов≥дь: 
749. ≈лектрон з енерг≥Їю E = 9 е¬ рухаЇтьс€ у позитивному напр€мку ос≥ x. ѕри €к≥й ширин≥ d потенц≥ального бар'Їра коеф≥ц≥Їнт прозорост≥ D = 0,1, €кщо висота U бар'Їра дор≥внюЇ 10 е¬? «образити на рисунку вигл€д хвильовоњ функц≥њ (њњ д≥йсну частину) у межах кожноњ з областей I, II, III (див. рис.1).
¬≥дпов≥дь:  нм.
нм.
750. ѕри €к≥й ширин≥ d пр€мокутного потенц≥ального бар'Їра коеф≥ц≥Їнт прозорост≥ D дл€ електрон≥в дор≥внюЇ 0,01? –≥зниц€ енерг≥й U - ≈ = 10 е¬.
¬≥дпов≥дь: d = 0,143 нм.
751. ≈лектрон з енерг≥Їю ≈ рухаЇтьс€ у позитивному напр€мку ос≥ х. ѕри €кому значенн≥ U - ≈, вираженому в електрон-вольтах, коеф≥ц≥Їнт прозорост≥ D = 10  , €кщо ширина d бар'Їра дор≥внюЇ 0,1 нм?
, €кщо ширина d бар'Їра дор≥внюЇ 0,1 нм?
¬≥дпов≥дь:  е¬.
е¬.
752. ≈лектрон з енерг≥Їю E = 9 е¬ рухаЇтьс€ у позитивному напр€мку ос≥ x. ќц≥нити ≥мов≥рн≥сть W того, що електрон пройде через потенц≥альний бар'Їр, €кщо його висота U = 10 е¬ ≥ ширина d = 0,1 нм.
¬≥дпов≥дь: W = 0,357.
753. ѕр€мокутний потенц≥альний бар'Їр маЇ ширину d = 0,1 нм. ѕри €к≥й р≥зниц≥ енерг≥й U - ≈ ймов≥рн≥сть W проходженн€ електрона через бар'Їр дор≥внюЇ 0,99?
¬≥дпов≥дь: U - ≈ = 0,95 . 10  е¬.
е¬.
754. ядро випром≥нюЇ α-частинки з енерг≥Їю E = 5 ће¬. ” першому наближенн≥ можна вважати, що α-частинки проход€ть через пр€мокутний потенц≥альний бар'Їр висотою U = 10 ће¬ ≥ шириною d = 5 фм. «найти коеф≥ц≥Їнт прозорост≥ D бар'Їра дл€ α-частинок.
¬≥дпов≥дь: D = 0,53.10-4.
755. ѕротон ≥ електрон пройшли однакову прискорювальну р≥зницю потенц≥ал≥в U = 10 к¬. ” ск≥льки раз≥в в≥др≥зн€ютьс€ коеф≥ц≥Їнти прозорост≥  дл€ електрона ≥
дл€ електрона ≥ 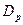 дл€ протона, €кщо висота U бар'Їра дор≥внюЇ 20 ке¬ ≥ ширина d = 0,1 пм?
дл€ протона, €кщо висота U бар'Їра дор≥внюЇ 20 ке¬ ≥ ширина d = 0,1 пм?
¬≥дпов≥дь:  .
.
756. ≈лектрон маЇ енерг≥ю ≈ = 10 е¬. ¬изначити, у ск≥льки раз≥в зм≥н€тьс€ його швидк≥сть υ, довжина хвил≥ де Ѕройл€ λ ≥ фазова швидк≥сть υф при проходженн≥ через потенц≥альний бар'Їр (див. рис.1) висотою U = 6 е¬.
¬≥дпов≥дь:  = 0,632;
= 0,632;  = 1,58;
= 1,58;  = 0,632.
= 0,632.
757. оеф≥ц≥Їнт в≥дбитт€ протона в≥д потенц≥ального бар'Їра ρ дор≥внюЇ 2,5.10  . ¬изначити, €кий в≥дсоток складаЇ висота U бар'Їра в≥д к≥нетичноњ енерг≥њ
. ¬изначити, €кий в≥дсоток складаЇ висота U бар'Їра в≥д к≥нетичноњ енерг≥њ  протон≥в, що падають на бар'Їр.
протон≥в, що падають на бар'Їр.
¬≥дпов≥дь:  = 2%.
= 2%.
758. ≈лектрон з енерг≥Їю ≈ = 10 е¬ падаЇ на потенц≥альний бар'Їр. ¬изначити висоту U бар'Їра, при €к≥й показник заломленн€ n хвиль де Ѕройл€ ≥ коеф≥ц≥Їнт в≥дбитт€ ρ чисельно зб≥гаютьс€.
¬≥дпов≥дь: U = 9,13 е¬.
759. ѕс≥-функц≥€ де€коњ частинки маЇ вигл€д  , де r Ц в≥дстань частинки в≥д силового центра; ј Ц константа. «найти: а) значенн€ коеф≥ц≥Їнта ј; б) середню в≥дстань r частинки в≥д центра.
, де r Ц в≥дстань частинки в≥д силового центра; ј Ц константа. «найти: а) значенн€ коеф≥ц≥Їнта ј; б) середню в≥дстань r частинки в≥д центра.
¬≥дпов≥дь:  .
.
760. ѕс≥-функц≥€ де€коњ частинки маЇ вигл€д  , де r Ц в≥дстань частинки в≥д силового центра; а Ц константа. «найти середню в≥дстань
, де r Ц в≥дстань частинки в≥д силового центра; а Ц константа. «найти середню в≥дстань 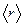 частинки в≥д центра.
частинки в≥д центра.
¬≥дпов≥дь:  .
.
761. ’вильова функц≥€, що описуЇ рух електрона в основному стан≥ атома водню, маЇ вигл€д  , де ј Ц де€ка стала;
, де ј Ц де€ка стала;  Ц перший бор≥вський рад≥ус. —ереднЇ значенн€ потенц≥альноњ енерг≥њ дл€ цього стану дор≥внюЇ
Ц перший бор≥вський рад≥ус. —ереднЇ значенн€ потенц≥альноњ енерг≥њ дл€ цього стану дор≥внюЇ 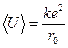 . «найти значенн€ сталоњ ј.
. «найти значенн€ сталоњ ј.
¬≥дпов≥дь:  .
.
762. Ќаписати р≥вн€нн€ Ўред≥нгера дл€ електрона, що перебуваЇ у воднепод≥бному атом≥.
¬≥дпов≥дь:  .
.
763. Ќаписати р≥вн€нн€ Ўред≥нгера дл€ л≥н≥йного гармон≥чного осцил€тора. ¬рахувати, що сила, €ка повертаЇ частинку до положенн€ р≥вноваги, F = kх (де k Ц коеф≥ц≥Їнт пропорц≥йност≥; х Ц зм≥щенн€).
¬≥дпов≥дь:  .
.
764. ѕровести нормуванн€ хвильовоњ функц≥њ  .
.
¬≥дпов≥дь:  .
.
765. „им обумовлена вимога ск≥нченност≥ ψ- функц≥њ?
766. –≥вн€нн€ Ўред≥нгера дл€ стац≥онарних стан≥в маЇ вигл€д 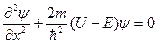 . ќбірунтувати, виход€чи з цього р≥вн€нн€, вимоги, що висувають до хвильовоњ функц≥њ, њњ неперервн≥сть ≥ неперервн≥сть першоњ пох≥дноњ в≥д хвильовоњ функц≥њ.
. ќбірунтувати, виход€чи з цього р≥вн€нн€, вимоги, що висувають до хвильовоњ функц≥њ, њњ неперервн≥сть ≥ неперервн≥сть першоњ пох≥дноњ в≥д хвильовоњ функц≥њ.
767. ≈лектрон у атом≥ водню описуЇтьс€ у основному стан≥ хвильовою функц≥Їю  . ¬изначити в≥дношенн€ ≥мов≥рностей
. ¬изначити в≥дношенн€ ≥мов≥рностей 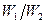 перебуванн€ електрона у сферичних шарах товщиною Δ r = 0,01a та рад≥усами
перебуванн€ електрона у сферичних шарах товщиною Δ r = 0,01a та рад≥усами  = 0,5 а ≥
= 0,5 а ≥  = 1,5 а.
= 1,5 а.
¬≥дпов≥дь:  .
.
768. ¬изначити короткохвильову межу суц≥льного спектра рентген≥вського випром≥нюванн€, €кщо рентген≥вська трубка працюЇ п≥д напругою U = 30 к¬.
¬≥дпов≥дь:  = 41 пм.
= 41 пм.
769. ќбчислити найб≥льшу довжину хвил≥  у -сер≥њ характеристичного рентген≥вського спектра сканд≥ю (z=21).
у -сер≥њ характеристичного рентген≥вського спектра сканд≥ю (z=21).
¬≥дпов≥дь:  = 304 пм.
= 304 пм.
770. ѕ≥д час досл≥дженн€ л≥н≥йчатого рентген≥вського спектра де€кого елементу було знайдено, що довжина хвил≥ λ л≥н≥њ  дор≥внюЇ 76 пм. ўо це за елемент?
дор≥внюЇ 76 пм. ўо це за елемент?
¬≥дпов≥дь: Z = 41; н≥об≥й.
771. яку найменшу р≥зницю потенц≥ал≥в  необх≥дно прикласти до рентген≥вськоњ трубки, антикатод €коњ покритий ванад≥Їм (Z = 23), щоб у спектр≥ рентген≥вського випром≥нюванн€ зТ€вились ус≥ л≥н≥њ -сер≥њ ванад≥ю? ћежа -сер≥њ ванад≥ю λ=226 пм.
необх≥дно прикласти до рентген≥вськоњ трубки, антикатод €коњ покритий ванад≥Їм (Z = 23), щоб у спектр≥ рентген≥вського випром≥нюванн€ зТ€вились ус≥ л≥н≥њ -сер≥њ ванад≥ю? ћежа -сер≥њ ванад≥ю λ=226 пм.
¬≥дпов≥дь:  = 5,5 к¬.
= 5,5 к¬.
772. ¬изначити енерг≥ю E фотона, €кий в≥дпов≥даЇ Kα-л≥н≥њ у характеристичному спектр≥ марганцю (Z = 25).
¬≥дпов≥дь: E = 5,9 ке¬.
773. ” атом≥ вольфраму електрон перейшов з ћ -шару на L -шар. Ѕеручи сталу екрануванн€ σ такою, що дор≥внюЇ 5,5, визначити довжину хвил≥ λ ф






