Завдання
1. Визначити сутність і значення основних економіко-математичних методів у господарській діяльності
2. Вивчити методику застосування економіко-математичних методів в аналізі господарської діяльності
3. Навчитися обирати оптимальний економіко-математичний метод відповідно до цілей економічного аналізу
5.1. Поняття і завдання економіко-математичних методів
Збільшення об'єктів аналітичного дослідження і функцій управління вимагає удосконалення аналізу господарської діяльності на основі застосування економіко-математичних методів.
Способи, що використовуються в економічному аналізі, потребують застосування математичного апарату різного ступеня складності, який класифікують за складністю застосовуваного інструментарію:
а) методи елементарної математики;
б) методи вищої математики.
Методи елементарної математики використовуються у звичайних традиційних економічних розрахунках при обґрунтуванні потреб у ресурсах, розробці планів, проектів, балансових розрахунках тощо.
В основі економіко-математичних методів лежить методика розрахунків вищої математики. Це пов'язано з невизначеністю господарської діяльності підприємства, що передбачає отримання приблизних (прогнозних) результатів, які можуть бути використані в управлінні підприємством.
Використання математичних методів у сфері управління (у тому числі економічних)- найважливіший напрям удосконалення систем управління. Перевагою використання математичних методів є прискорення проведення економічного аналізу, більш повний аналіз впливу факторів на результати діяльності, підвищення аналітичності обчислень.
Застосування математичних методів потребує:
Ø системного підходу до об'єкта дослідження, врахування взаємозв'язків і взаємовідносин з іншими суб'єктами господарської діяльності;
Ø розробки економічно-математичних моделей, що відображають кількісні показники господарської діяльності підприємства для найбільш повного та достовірного відображення процесу функціонування як підприємства, так і його структурних підрозділів;
Ø удосконалення системи інформаційного забезпечення управління підприємством з використанням сучасних комп'ютерних технологій.
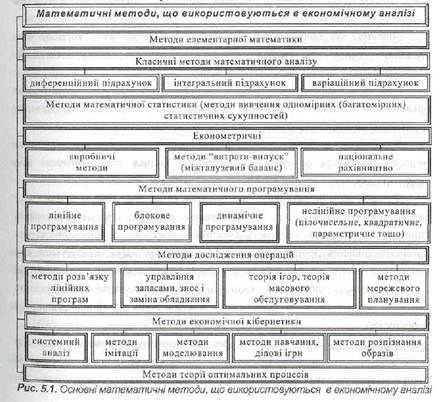 |
Для вирішення економічних завдань використовують різні методи, основні з яких наведені нарис. 5.1.
Кожен з математичних методів використовується для вирішення певного роду завдань. Наприклад, завдання управління запасами можуть вирішуватись за допомогою методів математичного програмування, теорії масового обслуговування.
5.2. Теорія ігор та її застосування в економічному аналізі
Теорія ігор - це теорія математичних моделей прийняття рішень в умовах конфлікту або невизначеності. Передбачається, що дії сторін у грі характеризуються певними стратегіями - набором правил, дій. Якщо перемога однієї сторони неминуче призводить до поразки іншої сторони, то говорять про антагоністичні ігри. Якщо набір стратегій обмежений, тоді гра називається матричною.
Рішення, які приймаються за допомогою теорії ігор, корисні при складанні планів в умовах можливих протидій конкурентів або невизначеності у зовнішньому середовищі.
При розв'язанні таких завдань визначаються наступні умови гри: правила гри і кількість учасників, можливі стратегії гравців і можливість отримання вигоди.
Теорія ігор, як розділ дослідження операцій, є теорією математичних моделей прийняття оптимальних рішень в умовах невизначеності або конфлікту декількох сторін, що мають різні інтереси.
У теорії ігор розрізняють такі поняття як вихідна стратегічна гра і власне статистична гра. У цій теорії першого гравця називають "природою". Під нею розуміють сукупність обставин, в яких доводиться приймати рішення другому гравцю - "статистику". Для стратегічної гри характерна повна невизначеність у виборі стратегії кожним гравцем, які діють на основі інформації, визначеної матрицею втрат. Дослідження стратегій проводиться за допомогою використання лінійних рівнянь і нерівностей.
Матричні методи аналізу.
Матричні методи аналізу застосовується для вивчення складних структур як на галузевому, так і на рівні підприємств і їх об'єднань.
Балансова модель — це система рівнянь, які характеризують наявність ресурсів (продуктів) у натуральному або грошовому вираженні та напрями їх використання. При цьому наявність ресурсів (продуктів) і потреба в них кількісно співпадають. В основу рішення таких моделей покладено методи лінійної алгебри, що й пояснює назву балансових методів і моделей, які називають матричними методами аналізу. Наочність зображення різних математичних процесів у матричних моделях і елементарні способи вирішення систем рівнянь дозволяють застосовувати їх у різних виробничо-господарських ситуаціях. Наприклад, відомо, що кожне підприємство поряд з основним виробництвом має допоміжне, що включає в себе ряд цехів. Допоміжні цехи надають послуги один одному та основному виробництву. Величина собівартості робіт і послуг кожного допоміжного цеху складається з собівартості робіт (послуг) інших допоміжних цехів. Щоб визначити витрати, пов'язані з використанням даним цехом робіт (послуг) інших цехів, потрібно одночасно з обсягом наданих робіт (послуг) знати їх собівартість. Але, у свою чергу, визначення їх собівартості неможливе без попереднього обчислення собівартості робіт (послуг), які цехи отримали один від одного.
Найпоширенішими є матричні ігри. Для вибору рішення застосовується платіжна матриця або матриця рішень. Це таблиця, присудок якої передбачає можливі рішення, а підмет - стан середовища, на яке не можна впливати. На перетині граф і рядків вказують результати рішення при даному стані середовища - "платежі". Вони можуть бути виражені в рядках витрат, прибутку, надходжень грошових коштів тощо.
Використання матричного методу, як методу економічного аналізу, отримало розповсюдження для порівняльної оцінки діяльності різних систем (Підприємств, структурних підрозділів тощо).
У результаті порівняльного аналізу визначається рейтинг систем, що аналізуються.
Розглянемо алгоритм використання матричного методу.
 |
Етап 1. Обґрунтування системи оціночних показників і формування Метриці вихідних даних аij, тобто таблиці, де в рядках відображаються системи підприємства (і), а в графах - показники (j = І, 2,..., т) (табл. 5.1).
 |
Етап 2. У кожній графі визначається максимальний елемент, який приймається за одиницю, після чого всі елементи графи аij діляться на максимальний елементеталонної системи і створюється матриця стандартизованих коефіцієнтів хij (табл. 5.2).
Етап 3. Всі елементи матриці підносяться до квадрату. Якщо значимість показників, що складають матрицю,с різною, то кожному показнику привласнюється ваговий коефіцієнт к, який визначається експертним шляхом.
 |
Рейтингова оцінка по кожній системі визначається за формулою:
 |
Етап 4. Отримані рейтингові оцінки Rj розміщуються у ранжированому порядку, що визначається економічним змістом показників, які складають рейтинг (табл. 5.3,).
Як бачимо з таблиці 5.3. підприємство "Україна" має найвищу рейтингову оцінку - 1,891.
Результати описаного порівняльного аналізу показників діяльності підприємств можуть використовуватись для визначення інвестиційної привабливості окремого підприємства.
Розглянуті методи економічного аналізу мають практичну значимістьі використовуються найчастіше в комплексі для оцінки будь-якого показника або сфери діяльності підприємства.
5.3. Особливості застосування теорії масового обслуговування в економічному аналізі
Теорія масового обслуговування на основі теорії ймовірностей досліджує математичні методи кількісної оцінки процесів масового обслуговування. Всім завданням, пов'язаним з масовим обслуговуванням, притаманний випадковий характер явищ, що досліджуються. Кількість вимог на обслуговування і часові інтервали між їх надходженням мають випадковий характер, проте в сукупності підпорядковуються статистичному закону великих чисел.
Теорія масового обслуговування розглядає імовірнісні моделі реальних систем обслуговування і використовується для мінімізації витрат у сферах обслуговування, виробництва, торгівлі. При цьому враховуються три фактори:
1) частота зміни кількості клієнтів або вимог;
2) імовірність значного попиту покупців;
3) спосіб визначення витрат очікування і покращання обслуговування.
Теорія масового обслуговування використовується у випадках, коли в масовому порядку надходять вимоги на обслуговування з наступним їх задоволенням. На практиці це може бути надходження сировини, матеріалів, напівфабрикатів, виробів на склад і їх видача зі складу тощо.
Основними елементамитеорії масового обслуговування є джерела вимог, їх вхідний і вихідний потік, канали обслуговування. Схематично вони представлені на рис. 5.2.
 |
Виконання вимоги в системі продовжується деякий точно невизначений період часу, після чого канал, що звільнився, знову готовий до прийняття вимог. Якщо в системі допускається формування черги вимог, які надійшли у момент, коли всі канали зайняті, вони стають у чергу і чекають звільнення зайнятих каналів.
Наведемо коротку класифікацію систем масового обслуговування (рис. 5.3).
 |
За наявності одного каналу обслуговування система масового обслуговування називається одноканальною, а якщо їх декілька - багатоканальною.
Якщо джерела вимог включені до системи, вона називається замкненою, інакше- розімкненою.
Залежно від допустимості і характеру формування черги розрізняють системи обслуговування з відмовами, з необмеженою чергою і змішаного типу.
Система обслуговування з відмовами має місце за умови неможливості формування черги. Вимога, яка прийшла в момент, коли всі канали зайняті, отримує відмову і не буде задоволена. Прикладами таких систем служать автоматичні телефонні станції, поточні лінії тощо.
Система масового обслуговування з необмеженою чергою є структурою, у якій дозволяється черга необмеженої довжини. У такій системі вимоги, які надійшли, будуть задоволені, хоча час очікування може бути досить тривалим.
У системі масового обслуговування змішаного типу можливі різні обмеження, наприклад, на максимальну довжину черги, час перебування вимоги в черзі тощо.
В системі з обмеженою чергою вимога отримує відмову, якщо приходить в момент, коли всі місця в черзі зайняті. Вимога, що потрапила до черги, обов'язково обслуговується. В системі масового обслуговування з обмеженим часом перебування в черзі вимога стає в чергу і очікує деякий час. Якщо вона протягом певного часу не потрапить до каналу обслуговування, звільняє чергу. Такий варіант обслуговування застосовується для моделювання вхідного контролю заготовок.
Якщо декілька систем з'єднати послідовно, таким чином, щоб вимоги, що задовільні в одній системі, переходили до наступної, виникає багатофазна система масового обслуговування (наприклад, послідовна обробка деталей на декількох видах обладнання), в протилежному випадку система однофазна.
Робота систем масового обслуговування ускладнюється тим, що вимоги надходять не регулярно, а через випадкові проміжки. Це призводить до того, Що в окремі інтервали часу система діє з перевантаженням, а в інші - недовантажена або навіть повністю простоює.
Основне завдання теорії масового обслуговування - виявити залежність показників ефективності системи від характеру вхідного потоку, дисципліни її обмеження черги, кількості, продуктивності та умов функціонування каналів з метою наступної її оптимізації. В якості критерію оптимальності застосовують максимум прибутку від експлуатації системи; мінімум сумарних втрат, пов'язаних з простоєм каналів; мінімум вимог в черзі і виходів вимог, які не обслуговувались; задану пропускну здатність тощо.
5.4. Інші прийоми економічного аналізу на базі математичної
статистики






