Розділ 1. МАТЕМАТИЧНІ ОСНОВИ СИНТЕЗУ ЛОГІЧНИХ СХЕМ
Для зображення інформації в комп'ютерах використовується двійкова система числення. Таким чином, всі операції, які виконує комп'ютер, проводяться на множині {0,1}. Ці перетворення зручно формально зображати за допомогою апарата двійкової логіки, який буй розроблений англійським математиком Джорджем Булем (1815-1864). Ця алгебраїчна структура є алгеброю і називається булевою алгеброю. Булева алгебра використовується при розв'язанні різних задач обробки інформації, при роботі з базами даних, в логічному програмуванні, при проектуванні інтелектуальних систем, для конструювання та аналізу роботи комп'ютерів та інших електронних пристроїв, У цьому розділі розглянуто основні властивості булевих функцій з аргументами з множини {0, 1} і способи зображення булевих функцій у вигляді виразів булевої алгебри. Булева функція може мати велику кількість змінних і знаків операцій, у той час, як може існувати інше, еквівалентне зображення даної функції, що має меншу кількість змінних і операцій. У наступних розділах буде описано методи одержання виразів з мінімальною кількістю змінних і знаків операцій.
Деякі поняття і визначення булевої алгебри
Булева (логічна) змінна – це така змінна, яка може приймати лише два значення: 0 і 1.
Логічні змінні, як і змінні звичайної алгебри, позначають буквами латинського алфавіту або якою-небудь буквою з різними індексами, наприклад, x, y, z, 
.
Булевою (логічною або перемикальною) функцією називається функція 
, яка, як і її n аргументів, може приймати лише два значення: 0 і 1.
Виявляється, що з допомогою булевих функцій можна описувати дію різного класу схем цифрової електроніки, а також правила функціонування таких схем. Такого типу схеми називають комбінаційними, оскільки сигнал на їх виході (0 або 1) визначається комбінацією сигналів (0 або 1) на їх входах. У випадку, коли булева функція використовується для опису перемикальної (контактної) схеми, її називають перемикальною.
Перемикальна схема – це пристрій із перемикачів (контактів) і провідників, які зв’язують два і більше полюсів (входів і виходів), частина з яких вхідні, а частина – вихідні.
Надалі булеві функції від n аргументів часто будемо записувати у вигляді 
. Це пов’язано із поданням n -розрядних двійкових чисел у вигляді полінома n -го степеня. Наприклад, двійкове число 101101 можна подати у вигляді полінома: 
. У цьому випадку степінь двійки відповідає номеру змінної.
Функція , яка залежить від n аргументів, називається n - місною і є повністю заданою (повністю визначеною), якщо вказані її значення для всіх булевих (двійкових) наборів значень аргументів.
Двійковим набором 
, де 
, називається сукупність значень аргументів 
булевої функції 
.
Кажуть, що функція 
істотно не залежить від змінної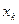 
, якщо 
.
У цьому випадку змінну 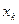називають неістотною змінною, у протилежному випадку – істотною.
Булеві функції, які істотно не залежать від деяких своїх змінних називаються виродженими, а ті, які істотно залежать від усіх своїх змінних – невиродженими.
Булеві функції, які невизначені на деяких наборах називаються неповністю визначеними функціями.
