Пріоритет операцій
Як уже відмічалось, кількість логічних функцій від n аргументів визначається числом  і швидко зростає при зростанні n. Наприклад, при n =3 таких функцій буде
і швидко зростає при зростанні n. Наприклад, при n =3 таких функцій буде 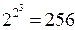 , а при n =4 їх буде уже
, а при n =4 їх буде уже 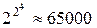 і т.д. Тому, як уже відмічалось, подання функцій за допомогою таблиць істинності з ростом числа змінних стає громіздким і незручним.
і т.д. Тому, як уже відмічалось, подання функцій за допомогою таблиць істинності з ростом числа змінних стає громіздким і незручним.
Розглянуті елементарні функції дозволяють одержувати складні булеві функції, в тому числі і для довільної кількості змінних, за допомогою узагальненої операції, яка називається операцією суперпозиції, яка полягає в підстановці замість змінних вхідної функції інших булевих функцій (в тому числі і змінних). Можливість такої підстановки зумовлена тим, що області значень їх змінних збігаються. Наприклад, маючи елементарні функції
 ,
,  ,
,
можна, користуючись принципом суперпозиції, одержати наступні нові функції:
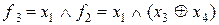 ,
, 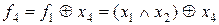 .
.
У розглянутому прикладі функцію  одержано шляхом підстановки у функцію
одержано шляхом підстановки у функцію  замість змінної
замість змінної  функцію
функцію  ; функцію
; функцію  – із функції
– із функції  шляхом підстановки у функцію
шляхом підстановки у функцію  замість змінної
замість змінної  функцію
функцію  .
.
Використання принципу суперпозиції дає можливість встановити зв’язки між елементарними функціями, тобто побудувати логічні вирази, які дозволяють записати одні елементарні функції через інші.
Розглянемо зв’язки між деякими елементарними функціями.
З табл. 8 виходить. що функція  на всіх наборах набуває значень, протилежних функції
на всіх наборах набуває значень, протилежних функції  . Справді, виконуючи принци суперпозиції, запишемо
. Справді, виконуючи принци суперпозиції, запишемо  .
.
Наведемо без пояснень деякі широко застосовувані співвідношення, які зв’язують елементарні функції:
1)  , 2)
, 2)  , 3)
, 3)  ,
,
4)  , 5)
, 5)  , 6)
, 6)  ,
,
7) 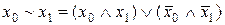 , 8)
, 8)  ,
,
9)  , 10)
, 10) 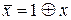 .
.
З наведених прикладів бачимо, що одна і та сама функція може бути задана різними формулами, наприклад, 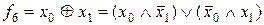 . Це означає, що серед цих формул є найпростіша. Пошук логічних формул, які найпростішим чином задають задану функцію, представляє практичний інтерес. Одним із способів побудови найпростіших логічних формул базується на використанні співвідношень (аксіом та законів) булевої алгебри.
. Це означає, що серед цих формул є найпростіша. Пошук логічних формул, які найпростішим чином задають задану функцію, представляє практичний інтерес. Одним із способів побудови найпростіших логічних формул базується на використанні співвідношень (аксіом та законів) булевої алгебри.
Часто при записі логічних формул використовують інфіксний запис, коли знаки операцій розташовані між змінними. Для запису виразів у інфіксній формі необхідно визначити порядок виконання операцій, що здійснюється за допомогою дужок або задання пріоритету операцій.
За відсутності дужок операції виконуються у такій послідовності: заперечення, кон’юнкція, диз’юнкція, імплікація та еквівалентність:
¯,  ~.
~.
Наявність у виразі дужок змінює звичайний порядок дій, при цьому в першу чергу виконуються операції в дужках.
Приклад 1. У заданій функції

опустити максимально можливе число дужок з урахуванням пріоритету операцій.
Розв’язання.  .
.






