Булева алгебра базується на деяких аксіомах, із яких виводяться основні закони для перетворення виразів, що містять булеві змінні. Обґрунтування цих аксіом підтверджується таблицями істинності для розглядуваних операцій. Кожна аксіома подана у двох формах: кон’юнктивній і диз’юнктивній, що випливає із принципу двоїстості логічних операцій, згідно якого операції кон’юнкції і диз’юнкції допускають взаємну заміну, якщо одночасно поміняти логічну 1 на 0, а 0 на 1; знак Ú на Ù, а знак Ù на Ú.
Аксіоми кон’юнкції, диз’юнкції і заперечення:
1. 
; 1. 0 Ù 0 = 0; 1. 0 Ú 0 = 0;
2. 
. 2. 0 Ù 1 = 0; 2. 0 Ú 1 = 1;
3. 1 Ù 0 = 0; 3. 1 Ú 0 = 1;
4. 1 Ù 1 = 1; 4. 1 Ú 1 = 1;
Закони булевої алгебри випливають із аксіом і також мають дві форми вираження: для кон’юнкції і для диз’юнкції.
Комутативні закони
а) 
; б) .
Сполучні закони
а) 
; б) 
.
Розподільні закони
а) 
; б) 
Закони поглинання
а)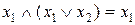 
; б) 
.
Закони склеювання
а)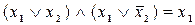 
; б)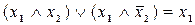 
.
Закон подвійного заперечення
.
Закони де Моргана
а) 
; б) 
або після інвертування лівих і правих частин:
в)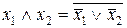 
; г) 
.
Зауважимо, що закони де Моргана є дійсними для будь-якої кількості змінних:
; 
.
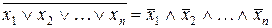Закони ідемпотентності
а) 
; б) 
.
Закони універсальної множини
а)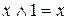 
; б)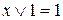 
.
Закони нульової множини
а)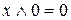 
; б)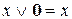 
.
Закони доповнення
а)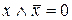 
; б) 
.
Правильність наведених законів легко доводиться за допомогою викладених вище аксіом або шляхом побудови таблиці істинності.
Доведемо, наприклад, справедливість розподільного закону (випадок б):
Спочатку виконаємо доведення скориставшись аксіомами:
.
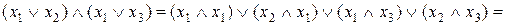
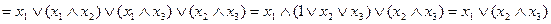Доведемо шляхом побудови таблиці істинності. Для цього побудуємо таблиці істинності для виразів, які знаходяться в лівій і правій частинах рівності. Результати обчислень наведено в табл. 9.
Таблиця 9
| 
| 
| 
| 
| 
| 
| 
|
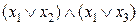
Співпадання значень у виділених стовпцях табл. 9 доводить справедливість рівності.
Аналогічно можна довести інші закони.
Із комутативного і асоціативного законів для диз’юнкції (кон’юнкції) випливає, що диз’юнкція (кон’юнкція) декількох змінних може виконуватись послідовно, причому порядок обчислення диз’юнкції не впливає на результат. Це дає можливість сформулювати такі правила:
1. Якщо в логічному добутку (кон’юнкції), що містить не менше двох співмножників, один із співмножників дорівнює нулю, то логічний добуток дорівнює нулю.
2. Якщо в логічному добутку, що містить не менше двох співмножників, є співмножник, який дорівнює одиниці, то цей співмножник можна вилучити.
3. Якщо в логічній сумі (диз’юнкції), що містить не менше двох доданків, є доданок, який дорівнює нулю, то цей доданок можна вилучити.
4. Якщо в логічній сумі, один із доданків дорівнює одиниці, то ця сума дорівнює одиниці.
Приклад 2. а) Довести, що 
Маємо
б). Довести, що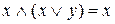 
. Маємо
в) Довести, що 
. Маємо
г) Довести, що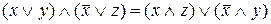 
. Маємо
.
Двоїстість
Означення 1. Логічна функція 
називається двоїстою до функції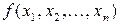 
, якщо 
.
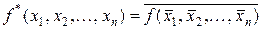Означення 2. Функція, двоїста сама до себе, тобто 
, називається самодвоїстою.
Правило побудови двоїстої функції. Для запису функції 
, двоїстої до функції 
, треба у функції всюди 0 замінити на 1, 1 – на 0, знак Ù – на Ú, а знак Ú – на Ù. Наведене правило побудови двоїстих функцій називається принципом двоїстості.
Приклад 3. Нехай, задано логічну функцію 
. Побудувати функцію двоїсту до заданої.
Розв’язання. а) Виходячи з означення двоїстості та застосувавши правило де Моргана два рази, одержимо
.
б) Скориставшись правилом побудови двоїстих функцій (принципом двоїстості) зразу одержимо, що 
.
Легко переконатись, що таблиця істинності двоїстої функції одержується з таблиці істинності для функції шляхом інвертування (заміною значень 0 на 1 та 1 на 0) значень функції й записом стовпчика інвертованих значень функції у зворотному порядку (див. два останні стовпці табл. 10)
Таблиця 10
| x | y | z | 
| 
|
| 
| 
| 
| 
| 
| ||
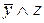
На підставі законів де Моргана можна вивести таке твердження: якщо функція двоїста до функції , то справедлива тотожність
.
Таким чином, заперечення функції можна знайти або за допомогою закону де Моргана, або заміною в функції двоїстої до заданої значення всіх змінних на протилежні – 
на 
і на 
, де 
.
Логічна функція є самодвоїстою (непарною), якщо на кожній парі протилежних наборів вона приймає протилежні значення, тобто
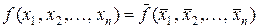або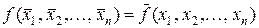 
.
Для двох змінних такими функціями є: 
.
Приклад 4. Користуючись таблицею істинності вияснити чи є функція 
самодвоїстою.
Розв’язання. Для побудови двоїстої функції скористаємось правилом побудови двоїстих функцій. Аналізуючи таблицю істинності (табл.11) легко переконатись, що побудована функція не є самодвоїстою, тобто: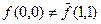 
, 
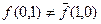і 
.
Таблиця 11
| x | y |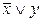 
| 
| 
| 
| 
| 
| |
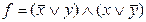
