Оценить параметры модели – I Клейна, используя данные таблицы 6.2

.

 

Таблица 6.2 – Исходные данные для построения модели –I Клейна

Годы	CN	Pt	Pt-1	W1	W2	I	Kt-1	Et	Et-1
	41,9	12,4	12,7	25,5	2,7	-0,2	182,8	45,6	44,9
	45,0	16,9	12,4	29,3	2,9	1,9	182,6	50,1	45,6
	49,2	18,4	16,9	34,1	2,9	5,2	184,5	57,2	50,1
	50,6	19,4	18,4	33,9	3,1	3,0	189,7	57,1	57,2
	52,6	20,1	19,4	35,4	3,2	5,1	192,7	61,0	57,1
	55,1	19,6	20,1	37,4	3,3	5,6	197,8	64,0	61,0

Продолжение таблицы 6.2

	56,2	19,8	19,6	37,9	3,6	4,2	203,4	64,4	64,0
	57,3	21,1	19,8	39,2	3,7	3,0	207,6	64,5	64,4
	57,8	21,7	21,1	41,3	4,0	5,1	210,6	67,0	64,5
	55,0	15,6	21,7	37,9	4,2	1,0	215,7	61,2	67,0
	50,9	11,4	15,6	34,5	4,8	-3,4	216,7	53,4	61,2
	45,6	7,0	11,4	29,0	5,3	-6,2	213,3	44,3	53,4
	46,5	11,2	7,0	28,5	5,6	-5,1	207,1	45,1	44,3
	48,7	12,3	11,2	30,6	6,0	-3,0	202,0	49,7	45,1
	51,3	14,0	12,3	33,2	6,1	-1,3	199,0	54,4	49,7
	57,7	17,6	14,0	36,8	7,4	2,1	197,7	62,7	54,4
	58,7	17,3	17,6	41,0	6,7	2,0	199,8	65,0	62,7
	57,5	15,3	17,3	38,2	7,7	-1,9	201,8	60,9	65,0
	61,6	19,0	15,3	41,6	7,8	1,3	199,9	69,5	60,9
	65,0	21,1	19,0	45,0	8,0	3,3	201,2	75,7	69,5
	69,7	23,5	21,1	53,3	8,5	4,9	204,5	88,4	75,7

 

где - потребление;

- текущий и лаговый незарплатный доход (прибыль), долл. США;

- заработная плата работников занятых в частном секторе, долл. США;

- заработная плата работников занятых в государственном секторе, долл. США;

- запас капитала на начало года, долл. США;

- чистые инвестиции, долл. США;

- текущий и лаговый частный продукт (равен как НД плюс косвенные налоги на бизнес минус ).

Проверим модель на идентифицируемость.

В модели 3 эндогенные переменные: , , . Следовательно, К=3.

И 6 предопределенных переменных: , , 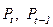, . Следовательно, М=6.

Проверим необходимое условие идентификации:

В первом уравнении m₁=3, k=1. 6-3=3>1-1=0. Следовательно, уравнение сверхидентифицированно.

Во втором уравнении m₂=3, k=1. 6-3=3>1-1=0. Следовательно, уравнение сверхидентифицированно.

В третьем уравнении m₃=2, k=1. 6-2=4>1-1=0. Следовательно, уравнение сверхидентифицированно.

Проверим достаточное условие идентификации:

В первом уравнении отсутствуют , , . Построим матрицу из коэффициентов при них в других уравнениях системы: .

Ранг данной матрицы равен 2=К-1=3-1. Следовательно, уравнение точно идентифицируемо.

Во втором уравнении отсутствуют , , , , . Построим матрицу из коэффициентов при них в других уравнениях системы: .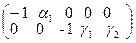

Ранг данной матрицы равен 2=К-1=3-1. Следовательно, уравнение точно идентифицируемо.

В третьем уравнении отсутствуют , , , , . Построим матрицу из коэффициентов при них в других уравнениях системы: .

Ранг данной матрицы равен 2=К-1=3-1. Следовательно, уравнение точно идентифицируемо.

Таким образом, можно сделать вывод, что исследуемая модель сверхидентифицированна и может быть решена двухшаговым методом наименьших квадратов (ДМНК).

1 Составим приведенную форму модели:

 

.

 

2 С помощью традиционного МНК оценим параметры приведенной формы модели. Получим следующие результаты (рисунок 6.3).

 

Рисунок 6.3 – Вывод итогов регрессионного анализа системы приведенных уравнений

 

Оцененная приведенная форма модели примет вид:

 

.

 

3 Определим расчетные значения переменной , т.к. она фигурирует в качестве фактора в структурной форме модели (рисунок 6.4).

Рисунок 6.4 – Расчетные и фактические значения переменной

4Определяем параметры каждого уравнения в отдельности традиционным МНК, используя в качестве факторов входящие в это уравнение предопределенные переменные и расчетные значения эндогенной переменной . Результаты представлены на рисунках 6.5 - 6.7.

Таким образом, система структурных уравнений примет вид:

 

.

 

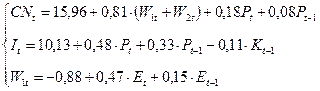Все полученные уравнения статистически значимы по F – критерию.

Рассчитаем по ним теоретические значения эндогенных переменных и проведем графический анализ (рисунок 6.8). Как видно на рисунке, теоретические значения незначительно отклоняются от фактических, следовательно полученная модель адекватна изучаемым процессам.

 

Рисунок 6.5 – Результаты МНК - оценивания первого уравнения

структурной формы ()

 

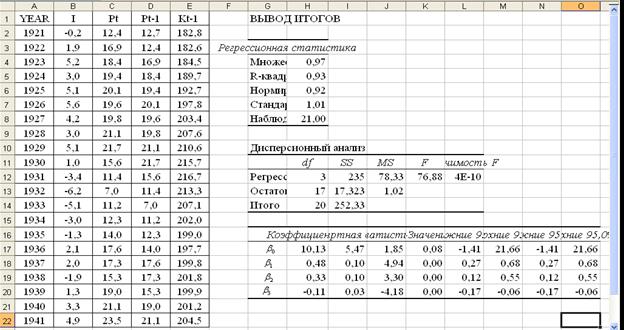
Рисунок 6.6 – Результаты МНК - оценивания второго уравнения

структурной формы ()

Рисунок 6.7 – Результаты МНК - оценивания третьего уравнения

структурной формы ()

 

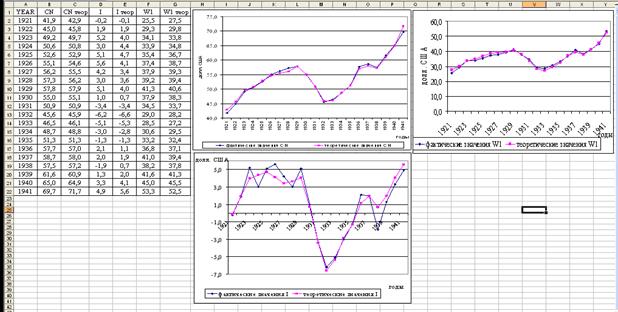
Рисунок 6.8 – Сравнительный графический анализ теоретических

и фактических значений эндогенных переменных