Корреляция и регрессия по первым разностям

Для оценки тесноты связи по первым разностям используем формулу:

.

где , - первые разности

Построим вспомогательную таблицу 5.10.

 

Таблица 5.10 – Расчет коэффициента корреляции

t	y	x
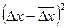
	325,69	15,69	-	-	-	-	-
	340,79	16,69	15,10	1,00	15,10	1,52	0,04
	349,39	17,69	8,60	1,00	8,60	59,81	0,04
	373,59	19,09	24,20	1,40	33,88	61,88	0,04
	389,79	20,79	16,20	1,70	27,54	0,02	0,24
	399,09	21,69	9,30	0,90	8,37	49,47	0,10
	421,49	23,09	22,40	1,40	31,36	36,80	0,04
	441,39	24,09	19,90	1,00	19,90	12,72	0,04
	458,29	25,19	16,90	1,10	18,59	0,32	0,01
	472,33	26,58	14,04	1,39	19,49	5,28	0,03
	489,02	27,81	16,70	1,23	20,48	0,13	0,00
Итого	4460,86	238,39	163,33	12,12	203,32	227,95	0,59
В среднем	405,53	21,67	16,33	1,21	20,33	22,80	0,06

 

Подставляя в формулу наши данные, получим:

 

.

 

Следовательно, можно сделать вывод о наличии прямой связи средней силы скорости ряда энерговооруженности 1 рабочего и скорости ряда выпуска продукции.

Для оценки параметров уравнения регрессии по первым разностям воспользуемся встроенной функцией MS Excel. Результаты оценивания представлены в приложении В.

Уравнение регрессии примет вид:

.

 

Оно показывает, что рост скорости энерговооруженности 1 рабочего на 1 кВт/ч, способствует росту скорости для ряда выпуска продукции на 13,6 тыс. тонн.

Прогнозирование осуществим по формуле:

 

.

 

Прогноз выпуска продукции на 2006 год, при ожидаемом увеличении энерговооруженности на 1 кВт/ч относительно 11 года, составит:

 

тыс. тонн.

 

Корреляция и регрессия по отклонениям от тренда

Коэффициент корреляции по отклонениям от тренда имеет вид:

 

,

где , - отклонения фактических значений ряда от тренда, т.е. , .

 

В качестве аппроксимирующей модели примем линейный тренд. Оценим параметры трендов с помощью встроенной функции MS Excel. Результаты представлены на рисунках 5.4 и 5.5.

 

Рисунок 5.4 – Динамика выпуска продукции

 

Рисунок 5.5 – Динамика энерговооруженности рабочих

 

 

Таблица 5.11 – Расчет коэффициента корреляции по остаточным величинам

t	y	x
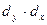
	325,69	15,69	322,04	15,54	3,65	0,15	0,55	13,33	0,02
	340,79	16,69	338,74	16,77	2,05	-0,08	-0,16	4,22	0,01
	349,39	17,69	355,43	17,99	-6,04	-0,30	1,83	36,53	0,09
	373,59	19,09	372,13	19,22	1,46	-0,13	-0,19	2,12	0,02
	389,79	20,79	388,83	20,45	0,96	0,34	0,33	0,92	0,12
	399,09	21,69	405,53	21,67	-6,44	0,02	-0,11	41,45	0,00
	421,49	23,09	422,23	22,90	-0,74	0,19	-0,14	0,54	0,04
	441,39	24,09	438,92	24,13	2,47	-0,04	-0,09	6,08	0,00
	458,29	25,19	455,62	25,35	2,67	-0,16	-0,43	7,12	0,03
	472,33	26,58	472,32	26,58	0,01	0,00	0,00	0,00	0,00
	489,02	27,81	489,02	27,81	0,01	0,00	0,00	0,00	0,00
	-	-	505,72	29,03	-	-	-	-	-
Итого	4460,86	238,39	4460,81	238,39	0,05	-0,01	1,59	112,32	0,32
В среднем	405,53	21,67	405,53	21,67	0,00	0,00	0,14	10,21	0,03

 

Тогда коэффициент корреляции рядов x и y по отклонениям от тренда составит:

 

.

 

Следовательно, связь между случайными отклонениями по ряду 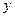и ряду прямая слабая.

Регрессия по отклонениям от трендаимеет вид . Оценим параметры модели с помощью встроенной функции MS Excel. Результаты оценивания представлены в приложении Г.

Уравнение регрессии примет вид:

.

 

Коэффициент регрессии означает, что случайные отклонения по ряду 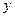в среднем в 18,55 раз выше случайных колебаний по ряду .

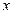Прогнозная модель по отклонениям от тренда имеет вид:

 

,

 

где - прогнозное значение результативного признака;

- прогноз по тренду результативного признака;

- прогнозное значение факторного признака;

- прогноз по тренду факторного признака.

 

Тогда, подставив соответствующие значения в модель, получим прогноз выпуска продукции на 12 год, при ожидаемой энерговооруженности =28,81 кВт/ч:

 

тыс. тонн.