Используя критерий Г. Чоу, выясним, можно ли считать одной и той же линейную регрессию для компаний с руководителями мужчинами и женщинами.
По 15 наблюдениям для компаний, руководителями которых являются мужчины, построим уравнение регрессии от факторов х2 и х3. Исходные данные представлены в таблице 2.6.
Таблица 2.6 – Исходные данные для построения модели по первой подвыборке (руководитель компании – мужчина)
| № предприятия | y | x2 | x3 | 
| 
|
| 2,5 | 5,3 | 16,5 | 3,0 | 0,219 | |
| 3,3 | 3,8 | 24,9 | 3,0 | 0,084 | |
| 2,3 | 5,1 | 9,2 | 2,8 | 0,288 | |
| 3,3 | 1,3 | 19,3 | 2,8 | 0,289 | |
| 4,2 | 6,1 | 40,8 | 3,4 | 0,620 | |
| 5,7 | 27,5 | 133,5 | 6,3 | 0,314 | |
| 3,2 | 5,6 | 32,9 | 3,3 | 0,003 | |
| 8,5 | 16,8 | 286,5 | 8,1 | 0,183 | |
| 3,5 | 5,3 | 16,4 | 3,0 | 0,285 | |
| 3,5 | 3,7 | 23,8 | 3,0 | 0,264 | |
| 3,4 | 3,6 | 54,6 | 3,5 | 0,006 | |
| 3,5 | 3,3 | 22,8 | 2,9 | 0,308 | |
| 0,7 | 0,4 | 50,4 | 3,2 | 6,304 | |
| 2,9 | 2,4 | 27,2 | 3,0 | 0,004 | |
| 3,6 | 3,2 | 25,2 | 3,0 | 0,388 | |
| Итого | 54,1 | - | - | 54,1 | 9,559 |
Результаты регрессионного анализа представлены в таблице 2.7.
Уравнение примет вид: 
. Расчетные значения по нему представлены в таблице 2.6, графа 5.
Построим модель регрессии по 10 предприятиям руководителями, которых являются женщины (исходные данные представлены в таблице 2.8).
Таблица 2.7 – Вывод итогов регрессионного анализа по первой подвыборке
| Регрессионная статистика | ||||||||||||
| Множественный R | 0,876 | |||||||||||
| R-квадрат | 0,767 | |||||||||||
| Нормированный R-квадрат | 0,728 | |||||||||||
| Стандартная ошибка | 0,892 | |||||||||||
| Наблюдения | ||||||||||||
| Дисперсионный анализ | ||||||||||||
| df | SS | MS | F | Значимость F | ||||||||
| Регрессия | 31,431 | 15,715 | 19,730 | 0,000 | ||||||||
| Остаток | 9,559 | 0,797 | ||||||||||
| Итого | 40,989 | |||||||||||
| Коэффициенты | Стандартная ошибка | t-статистика | P-Значение | Нижние 95 % | Верхние 95 % | |||||||
| 2,368 | 0,316 | 7,493 | 0,000 | 1,679 | 3,056 | ||||||
| 0,063 | 0,048 | 1,297 | 0,219 | -0,043 | 0,168 | ||||||
| 0,016 | 0,005 | 3,441 | 0,005 | 0,006 | 0,027 | ||||||
Таблица 2.8 – Исходные данные для построения модели для второй подвыборке (руководитель компании – женщина)
| № предприятия | y | x2 | x3 |
|
|
| 2,9 | 1,6 | 37,2 | 2,5 | 0,133 | |
| 0,4 | 1,6 | 2,3 | 0,063 | ||
| 2,9 | 2,2 | 10,3 | 2,3 | 0,333 | |
| 3,5 | 81,5 | 2,9 | 0,013 | ||
| 3,4 | 40,4 | 2,6 | 0,316 | ||
| 2,4 | 0,9 | 12,9 | 2,3 | 0,003 |
Продолжение таблицы 2.8
| 2,5 | 1,9 | 36,9 | 2,5 | 0,001 | |
| 2,7 | 4,2 | 53,8 | 2,7 | 0,001 | |
| 2,2 | 0,5 | 8,9 | 2,3 | 0,012 | |
| 2,3 | 1,6 | 31,1 | 2,5 | 0,035 | |
| Итого | 24,9 | - | - | 24,9 | 0,911 |
Результаты регрессионного анализа представлены в таблице 2.9.
Таблица 2.9 – Вывод итогов регрессионного анализа по второй подвыборке
| Регрессионная статистика | ||||||||||||
| Множественный R | 0,520 | |||||||||||
| R-квадрат | 0,271 | |||||||||||
| Нормированный R-квадрат | 0,062 | |||||||||||
| Стандартная ошибка | 0,361 | |||||||||||
| Наблюдения | ||||||||||||
| Дисперсионный анализ | ||||||||||||
| df | SS | MS | F | Значимость F | ||||||||
| Регрессия | 0,338 | 0,169 | 1,298 | 0,331 | ||||||||
| Остаток | 0,911 | 0,130 | ||||||||||
| Итого | 1,249 | |||||||||||
| Коэффициенты | Стандартная ошибка | t-статистика | P-Значение | Нижние 95 % | Верхние 95 % | |||||||
|
| 2,239 | 0,218 | 10,272 | 0,000 | 1,723 | 2,754 | ||||||
|
| 0,001 | 0,156 | 0,009 | 0,993 | -0,367 | 0,370 | ||||||
|
| 0,008 | 0,008 | 0,943 | 0,377 | -0,012 | 0,028 | ||||||
Модель регрессии примет вид: 
.
Теоретические значения по уравнению представлены в графе 5 таблицы 2.8.
По всем 25 предприятиям (таблица 2.10) рассчитаем уравнение регрессии для объединенной выборки.
Результаты регрессионного анализа представлены в таблице 2.11.
Таблица 2.10 – Исходные данные для построения объединенной модели с фиктивными переменными
| № предприятия | y | x2 | x3 |
|
| |
| 2,5 | 5,3 | 16,5 | 2,8 | 0,107 | ||
| 3,3 | 3,8 | 24,9 | 2,8 | 0,232 | ||
| 2,3 | 5,1 | 9,2 | 2,7 | 0,163 | ||
| 3,3 | 1,3 | 19,3 | 2,5 | 0,611 | ||
| 4,2 | 6,1 | 40,8 | 3,3 | 0,902 | ||
| 2,9 | 1,6 | 37,2 | 2,8 | 0,009 | ||
| 5,7 | 27,5 | 133,5 | 6,5 | 0,590 | ||
| 3,2 | 5,6 | 32,9 | 3,1 | 0,012 | ||
| 8,5 | 16,8 | 286,5 | 7,8 | 0,550 | ||
| 0,4 | 1,6 | 2,2 | 0,033 | |||
| 2,9 | 2,2 | 10,3 | 2,5 | 0,188 | ||
| 3,5 | 5,3 | 16,4 | 2,8 | 0,455 | ||
| 3,5 | 3,7 | 23,8 | 2,8 | 0,499 | ||
| 3,5 | 81,5 | 3,6 | 0,378 | |||
| 3,4 | 40,4 | 3,0 | 1,017 | |||
| 2,4 | 0,9 | 12,9 | 2,4 | 0,000 | ||
| 3,4 | 3,6 | 54,6 | 3,2 | 0,028 | ||
| 2,5 | 1,9 | 36,9 | 2,8 | 0,107 | ||
| 2,7 | 4,2 | 53,8 | 3,3 | 0,329 | ||
Продолжение таблицы 2.10
| 3,5 | 3,3 | 22,8 | 2,7 | 0,572 | |
| 0,7 | 0,4 | 50,4 | 2,9 | 4,804 | |
| 2,9 | 2,4 | 27,2 | 2,7 | 0,029 | |
| 3,6 | 3,2 | 25,2 | 2,8 | 0,689 | |
| 2,2 | 0,5 | 8,9 | 2,3 | 0,009 | |
| 2,3 | 1,6 | 31,1 | 2,7 | 0,173 | |
| Итого | 113,6 | 1098,6 | 12,487 |
Модель примет вид: 
. Теоретические значения по данной модели представлены в графе 5 таблицы 2.10.
Таблица 2.11 – Вывод итогов регрессионного анализа по всей совокупности
| Регрессионная статистика | ||||||||||||||
| Множественный R | 0,865 | |||||||||||||
| R-квадрат | 0,749 | |||||||||||||
| Нормированный R-квадрат | 0,726 | |||||||||||||
| Стандартная ошибка | 0,753 | |||||||||||||
| Наблюдения | ||||||||||||||
| Дисперсионный анализ | ||||||||||||||
| df | SS | MS | F | Значимость F | ||||||||||
| Регрессия | 37,233 | 18,616 | 32,798 | 0,000 | ||||||||||
| Остаток | 12,487 | 0,568 | ||||||||||||
| Итого | 49,720 | |||||||||||||
| Коэффициенты | Стандартная ошибка | t-статистика | P-Значение | Нижние 95 % | Верхние 95 % | |||||||||
|
| 2,124 | 0,198 | 10,704 | 0,000 | 1,712 | 2,535 | ||||||||
|
| 0,087 | 0,038 | 2,304 | 0,031 | 0,009 | 0,166 | ||||||||
|
| 0,015 | 0,004 | 3,818 | 0,001 | 0,007 | 0,022 | ||||||||
Рассчитываем F- критерий по формуле:
,
где 
- сумма квадратов отклонений фактических значений результативного признака от теоретических для объединенной выборки (таблица 2.10, итог графы 6);
- сумма квадратов отклонений фактических значений результативного признака от расчетных для первой подвыборки (таблица 2.6, итог графы 6);
- сумма квадратов отклонений фактических значений результативного признака от расчетных для второй подвыборки (таблица 2.8, итог графы 6).
Табличное значение критерия Фишера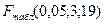 
составило 3,127. Так как расчетное значение критерия меньше табличного, то влияние фактора «пол» несущественно, и в качестве оценки регрессионной модели можно рассматривать уравнение регрессии, полученное по объединенной выборке.
