По исходным данным из лабораторной работы № 1, включив фиктивную переменную (таблица 2.3), построим матрицу парных коэффициентов корреляции (таблица 2.4).
Таблица 2.3 – Исходные данные для построения объединенной модели с фиктивными переменными
| № предприятия | y | x1 | x2 | x3 | x4 | x5 | Пол руководителя компании | D |
| А | ||||||||
| 2,5 | 38,2 | 5,3 | 16,5 | 29,4 | 1,2 | муж. | ||
| 3,3 | 20,3 | 3,8 | 24,9 | муж. |
Продолжение таблицы 2.3
| А | ||||||||
| 2,3 | 11,4 | 5,1 | 9,2 | 27,4 | 0,9 | муж. | ||
| 3,3 | 16,9 | 1,3 | 19,3 | 1,3 | муж. | |||
| 4,2 | 26,9 | 6,1 | 40,8 | 25,8 | 1,6 | муж. | ||
| 2,9 | 21,9 | 1,6 | 37,2 | 0,3 | жен. | |||
| 5,7 | 27,5 | 133,5 | 25,5 | 2,6 | муж. | |||
| 3,2 | 24,8 | 5,6 | 32,9 | 25,3 | 1,3 | муж. | ||
| 8,5 | 172,3 | 16,8 | 286,5 | 24,8 | 2,3 | муж. | ||
| 8,9 | 0,4 | 1,6 | 23,8 | жен. | ||||
| 2,9 | 13,7 | 2,2 | 10,3 | 23,8 | 1,5 | жен. | ||
| 3,5 | 5,3 | 16,4 | 23,5 | 1,8 | муж. | |||
| 3,5 | 20,3 | 3,7 | 23,8 | 14,7 | 1,9 | муж. | ||
| 16,7 | 3,5 | 81,5 | 21,6 | 1,3 | жен. | |||
| 26,4 | 3,4 | 40,4 | 21,2 | 1,5 | жен. | |||
| 2,4 | 13,7 | 0,9 | 12,9 | 20,6 | 0,2 | жен. | ||
| 3,4 | 33,9 | 3,6 | 54,6 | 1,1 | муж. | |||
| 2,5 | 19,3 | 1,9 | 36,9 | 18,3 | 1,7 | жен. | ||
| 2,7 | 24,6 | 4,2 | 53,8 | 13,9 | 2,1 | жен. | ||
| 3,5 | 19,6 | 3,3 | 22,8 | 17,8 | 2,1 | муж. | ||
| 0,7 | 28,3 | 0,4 | 50,4 | 17,7 | 1,4 | муж. | ||
| 2,9 | 20,4 | 2,4 | 27,2 | 17,7 | 1,8 | муж. | ||
| 3,6 | 20,3 | 3,2 | 25,2 | 17,6 | муж. | |||
| 2,2 | 11,1 | 0,5 | 8,9 | 16,4 | 1,3 | жен. | ||
| 2,3 | 22,4 | 1,6 | 31,1 | 15,7 | жен. | |||
| Итого | 810,3 | 113,6 | 1098,6 | 532,5 | 38,2 | - | - |
По матрице коэффициентов корреляции видно, что фиктивная переменная не коллинеарна с отобранными в лабораторной работе № 1 факторными переменными х2 и х3 (соответствующие коэффициенты составили 0,36 и 0,18). Следовательно, можно построить модель множественной регрессии, включив эти факторы. Результаты регрессионного анализа представлены в таблице 2.5.
Таблица 2.4 - Матрица парных коэффициентов корреляции по объединенной подвыборке
| y | x1 | x2 | x3 | x4 | x5 | d | |
| y | 1,00 | ||||||
| x1 | 0,85 | 1,00 | |||||
| x2 | 0,76 | 0,90 | 1,00 | ||||
| x3 | 0,83 | 0,91 | 0,71 | 1,00 | |||
| x4 | 0,27 | 0,25 | 0,35 | 0,12 | 1,00 | ||
| x5 | 0,50 | 0,50 | 0,54 | 0,43 | -0,03 | 1,00 | |
| d | 0,39 | 0,31 | 0,36 | 0,18 | 0,40 | 0,35 | 1,00 |
Модель примет вид: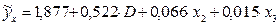 
. Уравнение регрессии значимо по F – критерию на 5 % уровне значимости. Оно показывает, что при одном и том же объеме использованного капитала и численности служащих, у предприятий руководителями которых являются мужчины, чистый доход больше в среднем на 0,522 млрд. долл., чем у остальных компаний. Однако, коэффициент при D статистически незначим (уровень значимости составил 0,118 > 0,05). Следовательно, влияние фактора «пол» оказалось несущественно, и есть основание считать, что модель одна и та же для компаний с руководителями мужчинами и женщинами.
Таблица 2.5 – Вывод итогов регрессионного анализа
| Регрессионная статистика | ||||||||||||
| Множественный R | 0,881 | |||||||||||
| R-квадрат | 0,777 | |||||||||||
| Нормированный R-квадрат | 0,745 | |||||||||||
| Стандартная ошибка | 0,727 | |||||||||||
| Наблюдения | ||||||||||||
| Дисперсионный анализ | ||||||||||||
| df | SS | MS | F | Значимость F | ||||||||
| Регрессия | 38,633 | 12,878 | 24,391 | 0,000 | ||||||||
| Остаток | 11,087 | 0,528 | ||||||||||
| Итого | 49,72 | |||||||||||
| Коэффициенты | Стандартная ошибка | t - статистика | P-Значение | Нижние 95 % | Верхние 95 % | |||||||
| 1,877 | 0,244 | 7,687 | 0,000 | 1,369 | 2,385 | ||||||
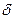
| 0,522 | 0,321 | 1,628 | 0,118 | -0,145 | 1,190 | ||||||
| 0,066 | 0,039 | 1,691 | 0,106 | -0,015 | 0,147 | ||||||
| 0,015 | 0,004 | 4,125 | 0,000 | 0,008 | 0,023 | ||||||
