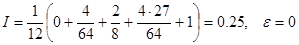Рассмотрим автономную систему 
и
функцию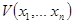 
.
Назовем эту функцию знакоположительной, если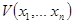 
,
знакоотрицательной, если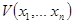 
Назовем функцию 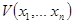положительно определенной, если
она знакоположительна,
Назовем функцию 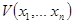отрицательно определенной, если
она знакоотрицательна,
Назовем функцию 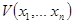знакоопределенной, если она является отрицательно определенной или положительно определенной.
Введем производную функции 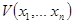в силу системы 
: 
. Заметим, что 
. Поэтому, если 
, то угол между градиентом V и вектором правых частей системы тупой. Следовательно, убывание функции V соответствует движению по фазовым траекториям внутрь линии уровня 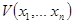=С.
На этом основан метод функций Ляпунова. Этот метод сводится к трем теоремам Ляпунова.
Теорема Ляпунова об устойчивости. Пусть существует функция 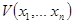(функция Ляпунова), положительно определенная и имеющая знакоотрицательную 
в некоторой окрестности точки 
.
Тогда тривиальное решение автономной системы 
устойчиво по Ляпунову.
Теорема Ляпунова об асимптотической устойчивости. Пусть существует функция 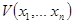, положительно определенная и имеющая отрицательно определенную в некоторой окрестности точки .
Тогда тривиальное решение автономной системы асимптотически устойчиво по Ляпунову.
Теорема Ляпунова о неустойчивости. Пусть 
. Пусть знакоопределена в некоторой окрестности точки . Если в любой окрестности точки найдутся такие точки, в которых знак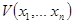и и совпадают, то тривиальное решение автономной системы неустойчиво.
Пример. 
Выберем 
положительно определена, отрицательно определена. Поэтому тривиальное решение асимптотически устойчиво.
Пример. 
Выберем
и положительно определены, поэтому тривиальное решение неустойчиво.
Лекция 25. Приближенное вычисление интеграла.
Часто нужно вычислить интеграл 
, а аналитически это сделать невозможно (интеграл не берется) или слишком громоздко. Тогда применяют приближенные методы вычисления интеграла на отрезке, по которым пишут алгоритмы и программы реализации этих методов на ЭВМ. Численный расчет дает значение интеграла с некоторой погрешностью, которая зависит как от погрешности метода, так и от погрешности вычислений. Чаще всего рассматривают равномерную сетку, разбивая отрезок 
на отрезки длины шагом h: 
.
Формулы прямоугольников.
Обозначим 
. Заменим интеграл интегральной суммой, вычисляя площадь под графиком функции как сумму площадей прямоугольников с основанием h, высотами 
.
Если на первом отрезке высоту прямоугольника можно выбрать как 
, тогда на последнем отрезке высота прямоугольника 
. Получим первую формулу прямоугольников
.
Если на первом отрезке высоту прямоугольника можно выбрать как 
, тогда на последнем отрезке высота прямоугольника 
. Получим вторую формулу прямоугольников
.
Оценим погрешность формул прямоугольников. Разложим 
в ряд Тейлора и оценим остаточный член.
Для первой формулы прямоугольников
где 
.
Для второй формулы прямоугольников
где .
Таким образом, обе формулы прямоугольников дают погрешность порядка h и являются формулами первого порядка точности.
Можно повысить точность формулы прямоугольников за счет вычисления функции в серединах отрезков разбиения. Получаем третью формулу прямоугольников
.
Оценим погрешность этой формулы.
+ 
+0+ 
Таким образом, погрешность третьей формулы прямоугольников не превышает , где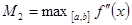 
. Эта формула прямоугольников имеет второй порядок точности.
Формула трапеций.
Сложим первую и вторую формулы прямоугольников и разделим пополам. Получим формулу трапеций
Поясним название формулы. Приблизим площадь под графиком функции на отрезке 
площадью трапеции 
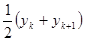. Суммируя площади по всему отрезку интегрирования, получим
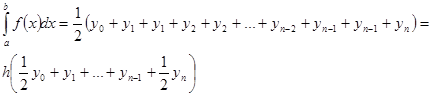
Аппроксимируем функцию кусочно – линейной функцией, значения которой совпадают с значениями функции в точках разбиения. Площадь под графиком кусочно – линейной функции на отрезке составит
. Суммируя площади по всему отрезку интегрирования, получим вновь формулу трапеций.
Можно показать, что формула трапеций – формула второго порядка точности. Погрешность вычисления интеграла с помощью этой формулы (это можно показать) не превышает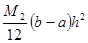 
, т.е. в два раза больше, чем по третьей формуле прямоугольников.
Формула Симпсона.
Аппроксимируем функцию на отрезке разбиения квадратичной функцией 
так, чтобы
Лемма. 
.
Докажем лемму для 
. Сделаем замену 
.
Тогда формула сведется к следующей:
.
Левая часть 
Правая часть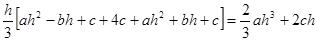 
. Лемма доказана.
Разобьем теперь отрезок интегрирования на 2n частей, (
). Применим лемму к отрезкам 
, 
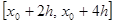,..., получим формулу Симпсона
.
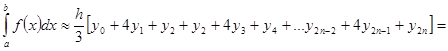
Можно показать, что формула Симпсона – формула четвертого порядка точности, ее погрешность не превосходит 
, где 
. Это означает, что при интегрировании многочлена третьей степени формула Симпсона точна, ее погрешность равна нулю.
Пример. Вычислить приближенно I = 
с шагом 
.
1 формула прямоугольников 
,
2 формула прямоугольников 
,
3 формула прямоугольников 
,
Формула трапеций 
.
Формула Симпсона 
