Рассмотрим сначала уравнение второго порядка
1) Пусть правая часть представляет собой квазиполином 
.
Ищем частное решение в виде 
. Здесь 
- полином n-ой степени, 
- полином, степень которого надо определить.
, 
.
а) Если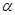 
- не корень характеристического уравнения, то 
, и многочлен надо выбирать той же степени, что и , т.е. степени n.
б) Если 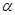- простой корень характеристического уравнения, то 
. В этом случае многочлен 
надо выбирать той же степени, что и , т.е. степени n. Тогда степень многочлена надо выбирать равной n+1. Однако при дифференцировании производная свободного члена (постоянной) равна нулю, поэтому можно выбирать в виде = 
.
в) Если 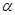- кратный корень характеристического уравнения, то 
. В этом случае многочлен 
надо выбирать той же степени, что и , т.е. степени n. Тогда степень многочлена надо выбирать равной n+2. Однако при двукратном дифференцировании производная не только свободного члена равна нулю, но и производная линейного члена равна нулю. Поэтому можно выбирать в виде = 
.
Пример. 
, 
, 
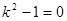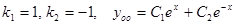
- не корень характеристического уравнения, поэтому частное решение надо искать в том же виде, что и правая часть, 
. Подставляем в неоднородное уравнение с правой частью 
.
.
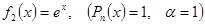. Корень 
содержится один раз среди корней характеристического уравнения, поэтому частное решение ищется в виде 
.
Подставляем в неоднородное уравнение с правой частью 
.
.
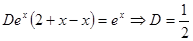
Суммируя оба частных решения, получаем частное решение неоднородного уравнения для исходной правой части:
.
Общее решение неоднородного уравнения будет
.
2) Правая часть имеет вид 
1) Если 
не корни характеристического уравнения, то частное решение ищется в том виде, в котором задана правая часть:
,
где 
- полиномы степени m – максимальной из степеней полиномов 
.
б) Если - пара корней характеристического уравнения, то частное решение ищется в виде
,
Пример. 
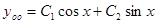
Пара корней = 
- пара корней характеристического уравнения.
Подставляем в неоднородное уравнение, получаем
, откуда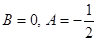 
, 
Рассмотрим неоднородное уравнение n-го порядка, покажем, как в нем применять метод подбора формы частного решения.
Здесь ситуация сложнее, так как в характеристическом уравнении n корней, действительные корни и комплексно сопряженные, простые и кратные корни.
- Пусть правая часть неоднородного уравнения имеет вид 
1) Если 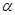не является корнем характеристического уравнения, то частное решение неоднородного уравнения ищется в том же виде, что и правая часть 
.
2) Если 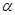- корень характеристического уравнения r-ой кратно сти, то частное решение неоднородного уравнения ищется в виде 
.
- Пусть правая часть неоднородного уравнения имеет вид
а) Если пара комплексно сопряженных корней не является корнями характеристического уравнения, то частное решение неоднородного уравнения ищется в том же виде, что и правая часть
, где степень m многочленов – максимальная из степеней многочленов .
1) Если пара комплексно сопряженных корней является корнями характеристического уравнения r-ой кратности, то частное решение неоднородного уравнения ищется в виде
.
Пример.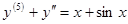 
,
.
. содержится в корнях характеристического уравнения 2 раза, поэтому 
. Подставляя это частное решение в неоднородное уравнение с правой частью , получим 
. Корни не содержатся в корнях характеристического уравнения, поэтому 
. Подставляя это частное решение в неоднородное уравнение с правой частью 
, получим 
.
. 
.
+ 
.
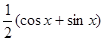Пример. 
.
содержится в корнях характеристического уравнения 3 раза, поэтому 
.
. Корни (пара корней) содержатся в корнях характеристического уравнения один раз, поэтому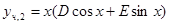 
. Неопределенные коэффициенты определяются, как и выше, подстановкой в уравнение и сравнением коэффициентов при одинаковых степенях x, при sinx, cosx, xsinx, xcosx.
