Неоднородную систему линейных дифференциальных уравнений можно записать в виде
.
Однородную систему линейных дифференциальных уравнений можно записать в виде
.
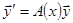Все теоремы для линейных систем аналогичны соответствующим теоремам для линейных дифференциальных уравнений высших порядков. Этого и следовало ожидать, так как система дифференциальных уравнений сводится к дифференциальному уравнению высшего порядка.
Теоремы о свойствах решений однородной и неоднородной системы.
Если 
- решения однородной системы, то 
- решения однородной системы.
Если 
- решения однородной и неоднородной систем, то 
- решение неоднородной системы.
Если 
- решения неоднородной системы, то 
- решение однородной системы.
Доказательство.
,
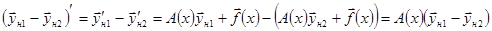
Теорема. Множество решений линейной однородной системы есть линейное пространство.
Из теорем о свойствах решений видно, что операции сложения и умножения на число на решениях однородной системы определены корректно.
Легко проверяется ассоциативность по сложению, существования «нуля» – тривиального решения 
, существование «противоположного элемента» 
, коммутативность по сложению. Отсюда следует, что решения однородной системы образуют коммутативную группу по сложению (абелев модуль) (4 аксиомы линейного пространства). Существует единица – число, справедлива ассоциативность по умножению на число (еще 2 аксиомы).
Наконец, справедлива дистрибутивность по сложению решений и чисел (последние 2 аксиомы). Таким образом, выполнены все 8 аксиом для корректно введенных операций сложения решений и умножения решения на число. Следовательно, множество решений однородной системы образует линейное пространство. Заметим, что точно так же доказывалась аналогичная теорема для дифференциального уравнения n-ого порядка.
Функции 
называются линейно независимыми, если
.
Функции называются линейно зависимыми, если
.
Введем определитель Вронского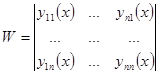 
, по столбцам которого расположены векторы 
, введем также матрицу 
.
Теорема. Если функции линейно зависимы, то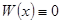 
.
Доказательство. Так как функции линейно зависимы, то одна из них линейно выражается (тождественно) через остальные, поэтому соответствующий столбец определителя Вронского линейно выражается через остальные. Тогда по свойству определителя .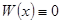
Теорема. Пусть - решения однородной системы и 
, тогда решения линейно зависимы.
Доказательство. Т.к. 
, то его столбцы в 
линейно зависимы, т.е. 
.
Рассмотрим решение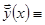 
(с теми же коэффициентами).
- решение однородной системы как линейная комбинация решений однородной системы (теоремы о свойствах решений). Начальные условия для этого решения в точке , как показано выше, нулевые. Но есть решение однородной системы (тривиальное решение ), имеющее те же начальные условия. Следовательно, по теореме Коши решение и есть тривиальное решение. Тогда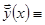 
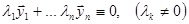, следовательно, решения линейно зависимы.
Следствие. Равенство определителя Вронского нулю для решений однородной системы хотя бы в одной точке – критерий линейной зависимости решений, отличие определителя Вронского от нуля для решений однородной системы хотя бы в одной точке – критерий линейной независимости решений.
Доказательство. Пусть , тогда решения линейно зависимы. Если решения линейно зависимы, то 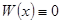по теореме о равенстве определителя Вронского нулю для системы линейно зависимых функций. Заметим, что тогда 
.
Пусть 
, если решения линейно зависимы, то 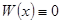(противоречие). Пусть решения линейно независимы. Если , тогда решения линейно зависимы (противоречие).
Теорема. Размерность пространства решений однородной системы равна n.
Доказательство. Надо доказать 1) существуют n линейно независимых решений однородной системы, 2) любое решение однородной системы линейно выражается через эти линейно независимые решения.
1) В любой точке 
для однородной системы выполнены условия теоремы Коши, следовательно, через любую такую точку пройдет единственная интегральная кривая – график решения однородной системы. Зададим такие точки – начальные условия, которые по теореме Коши определят решения 
.
Эти решения линейно независимы, так как 
.
Существование n линейно независимых решений однородной системы доказано.
2) Рассмотрим произвольное решение однородной системы . В точке вектор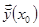 
разлагается по естественному базису
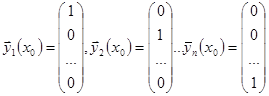.Поэтому 
Рассмотрим решение 
- линейную комбинацию этих линейно независимых решений. Оно имеет те же начальные условия, что и выбранное произвольное решение . Следовательно, по теореме Коши выбранное произвольное решение и есть (тождественно равно) . Поэтому произвольное решение линейно выражается через выбранные линейно независимые решения. Теорема доказана.
Любые n линейно независимых решений однородной системы представляют собой базис в пространстве решений и называются фундаментальной системой решений однородной системы.
Матрица 
, составленная из этих решений 
, называется фундаментальной матрицей однородной системы.
