Запишем уравнения системы в нормальной (покоординатной) форме
................................
и запишем эти уравнения в симметричном виде
.
Или, заменяя переменные и правые части 
,
получим симметричную форму записи системы
.
На переходе к симметричной форме записи основан метод интегрируемых комбинаций, которым иногда удается получить один или несколько первых интегралов и понизить тем самым порядок системы или решить ее.
Пример. 
, 
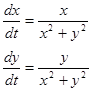Автономные системы и свойства их решений.
Система называется автономной, если в ее правую часть не входит явно независимая переменная: 
.
Решение автономной системы можно рассматривать в пространстве координат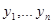 
, которое принято называть фазовым пространством. Проекция интегральной кривой на это пространство называется фазовой траекторией (или просто траекторией). Вообще говоря, любую систему можно сделать автономной, вводя дополнительную фазовую координату – независимую переменную 
и дополнительное уравнение 
. Фазовое пространство такой системы принято называть расширенным фазовым пространством.
Свойства решений автономных систем.
1) Если 
- решение системы, то и 
тоже решение.
.
Следствие. Фазовая траектория - это та же фазовая траектория, что и .
В самом деле, любая точка 
первой фазовой траектории является точкой 
второй фазовой траектории и наоборот.
2) Две фазовых траектории либо не имеют общих точек, либо совпадают.
Пусть две различных фазовых траектории 
имеют общую точку 
. Рассмотрим решение 
.
. Следовательно, по теореме Коши 
. Но 
- это траектория 
, сдвинутая на 
по аргументу. По следствию, обе фазовые траектории являются одной фазовой траекторией.
Следствие. Множество фазовых траекторий автономной системы в фазовом пространстве представляет собой совокупность непересекающихся кривых.
Точка 
называется точкой покоя (точкой равновесия) автономной системы, если 
.
3) Если точка - точка покоя, то 
- решение системы.
В самом деле, 
.
4) Любая фазовая траектория автономной системы есть траектория одного из трех типов:
1) гладкая, не самопересекающаяся кривая,
2) замкнутая гладкая кривая,
3) точка покоя.
Фазовый поток.
Рассмотрим решение задачи Коши автономной системы 
. Определим фазовый поток как оператор 
сдвига (по аргументу 
) по фазовым траекториям системы 
= .
Рассмотрим некоторую область 
фазового пространства (фазовым) объемом 
. Фазовый поток переводит эту область в область 
объемом 
.
Справедлива теорема Лиувилля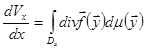 
.
Здесь мерой 
в фазовом пространстве может служить фазовый объем 
, 
(дивергенция векторного поля правых частей системы или след матрицы Якоби). Левая часть этой формулы представляет собой изменение фазового объема в единицу «времени» – аргумента, т.е. известный из теории поля поток векторного поля правых частей системы – фазовых скоростей. Приведенная формула аналогична формуле Остроградского – Гаусса в теории поля.
Если 
, то 
.
Если 
, то 
, что дает формулу для определения фазового объема 
, что совпадает с формулой Остроградского – Лиувилля определителя Вронского для линейных автономных систем. Поэтому определитель Вронского имеет смысл фазового объема (определитель всегда имеет смысл некоторого объема, вспомним хотя бы смысл смешанного произведения векторов).
