Введем понятие направляющего вектора прямой, это любой ненулевой вектор, параллельный данной прямой 
= 
. Очевидно, что точка 
(
, 
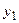) лежит на этой прямой тогда и только тогда, когда векторы 
= 
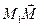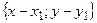и = коллинеарны, т. е., когда координаты этих векторов пропорциональны:
(14.4)
– каноническое уравнение прямой.
(Отношение следует понимать как 
,
т. е. если l = 0, а m ¹ 0, то х – х 1 = 0).
Отсюда уравнение прямой, проходящей через две данные точки (х 1, у 1), 
(х 2 ,у 2):
(14.5)
Пример 14.2. Составить уравнение прямой, проходящей через точки М (—1; 3) и N (2; 5).
. Решение. В уравнении 
берем 
, 
, 
, 
. Получаем 
или 
. Итак, искомое уравнение имеет вид 2 х -3 у +11=0.
Пример 14.3. Составить каноническое уравнение медианы АЕ треугольника, вершинами которого являются точки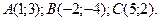 
Решение. Медиана АЕ делит сторону ВС пополам. Тогда, используя формулу для нахождения координат точки, делящей отрезок в заданном соотношении (4.9), найдем координаты точки Е.
Зная координаты точки 
и координаты вершины 
, составим каноническое уравнение прямой, проходящей через две точки
. Тогда 
или 
- каноническое уравнение медианы АЕ.
Пример 14.4. Даны вершинытреугольника: 
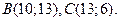Составить уравнение биссектрисы угла А.
Решение. Пусть точка D – точка пересечения биссектрисы со стороной ВС. Из свойства биссектрисы внутреннего угла
треугольника следует, что 
.Но 
,
Следовательно, 
Так как известно отношение, в котором точка D делит отрезок ВС, токоординаты точки D определятся по формулам 
, или 
, т.е. 
. Задача сводится к составлению уравнения прямой, проходящей через точки А и D:
, т.е.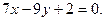 
Параметрические уравнения прямой.
Примем за параметр 
величину = t, тогда область определения t: -¥ < t < ¥. Мы получим х – х1 = lt; у – у1 = mt и параметрическое уравнение прямой
х = 
у = 
(14.6)
Уравнение прямой с угловым коэффициентом.
Тангенс угла наклона прямой к оси 
назовем угловым коэффициентом этой прямой: 
.
Уравнение прямой, проходящей через точку М 1(х 1, у 1) и имеющей заданный угловой коэффициент k, запишется в виде: у – у1 = k(х – х1) (5.7)
Если обозначить постоянную у1 – kx1 = b, то (5.7) примет вид
у = kx + b (14.8)
Пример 14.5. Составить уравнение прямой, отсекающей на оси ординат отрезок b= - 3 и образующей с положительным направлением оси абсцисс угол α = 
.
Решение. Находим угловой коэффициент: 
. Воспользовавшись уравнением прямой с угловым коэффициентом, получаем 
; освобождаясь от знаменателя и перенося все члены в левую сторону, получаем общее уравнение прямой 
.
Угол между двумя прямыми.
.Пусть прямые заданы уравнениями с угловым коэффициентом у = k 1 х+ b 1 и у = k 2 x + b 2; и 
= - угол между прямыми. Тогда
(14.9)
Прямые параллельны, если 
= 0, и условие параллельности
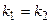(14.10)
Условие перпендикулярности – это условие того, что tg j не существует, т.е. 1 + 
= 0, отсюда условие перпендикулярности
(14.11)
Пример 14.6. Определить угол между прямыми
1) у =2 x +5 и у =-3 х +1:
2) 
и 
Решение. 1) В формуле 
принимаем 
, 
, тогда 
, т. e 
.
.2) Здесь 
, 
. Так как 
, то прямые перпендикулярны.
Пример. 14.7. Даны уравнения высот треугольника АВС: x+y -2 = 0; 9 x - 3 y -4=0 и координаты вершины A (2; 2). Составить уравнения сторон треугольника.
Решение. Легко убедиться в том, что вершина А не лежит ни на одной из заданных высот: ее координаты не удовлетворяют уравнениям этих высот.
Пусть 9 x – 3 у – 4 = 0 - уравнение высоты ВВ 1 и x+y -2=0 - уравнение высоты СС 1. Составим уравнение стороны АС, рассматривая ее как прямую, проходящую через точку А и перпендикулярную высоте ВВ 1. Так как угловой коэффициент высоты ВВ 1 равен 3, то угловой коэффициент стороны АС равен -1/3, т. е. k AC=-1/3. Воспользовавшись уравнением прямой, проходящей через данную точку и имеющей данный угловой коэффициент, получим уравнение стороны АC: y -2=-1/3(x -2), или x + 3 y – 8 = 0. Аналогично получаем k 
, k AB=1 и сторона АВ определится уравнением у – 2 = x - 2, т. е. у = х. Решив совместно уравнения прямых АВ и ВВ 1 а также прямых АС и СС 1, найдем координаты вершин треугольника В и С: В (2/3;2/3) и С (-1;3). Остается составить уравнение стороны ВС:
, т.е.7 x + 5 y – 8 = 0.
Вопросы для самопроверки
1. Как записывается общее уравнение прямой на плоскости?
2. Как записываются параметрические уравнения прямой на плоскости?
3. Что называется угловым коэффициентом прямой на плоскости и каков его геометрический смысл в декартовой прямоугольной системе координат?
4. Как записывается уравнение прямой, проходящей через две точки на плоскости?
5. Как вычисляются углы между двумя прямыми на плоскости? Каковы условия параллельности и перпендикулярности двух прямых на плоскости?
