1. Найти угол между прямой 
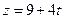и плоскостью 
.
Ответ. 
.
2. При каком значении 
прямая 
параллельна плоскости 
.
Ответ. 
.
3. При каких значениях B и D прямая 
лежит в плоскости 
?
Ответ. B =2 и D =8.
4. При каких значениях 
и 
прямая 
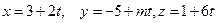перпендикулярна плоскости 
?
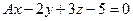Ответ.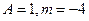 
.
5. Найти точку пересечения прямой и плоскости:
1) 
, 
2) 
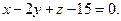
3) 
Ответ. 1) (2; -3; 6); 2) прямая, параллельная плоскости; 3) прямая лежит на плоскости.
6. Найти точку Q, симметричную точке Р (4; 1; 6) относительно прямой
Ответ. Q (2; - 3; 2).
7. Найти точку Q, симметричную точке Р (2; -5; 7) относительно прямой, проходящей через точки М 1(5; 4;6)и
М 2(-2;-17; - 8).
Ответ. Q (4; 1; -3).
8. Найти проекцию точки Р (5; 2; -1) на плоскость
.
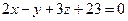Ответ. (1; 4; -7).
9. Найти точку Q, симметричную точке Р (1; 3; -4) относительно плоскости 
.
Ответ. Q (-5; 1; 0).
10. Вычислить расстояние d от точки Р (2 3;-1) до следующих прямых:
1) 
2) 
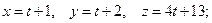
3) 
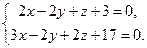
Ответ. 1) 21; 2) 6; 3) 15.
11. Убедившись, что прямые
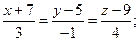
параллельны, вычислить расстояние между ними.
Ответ. 25
12. Составить уравнение плоскости, проходящей через точку Р (1; 2;-3) параллельно прямым
Ответ. 
.
13. Вычислить кратчайшее расстояние между двумя прямыми в каждом из следующих случаев:
1) 
.
2) 
.
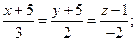
Ответ. 1) 3; 2) 7.
Занятие 14. Прямая на плоскости
Общее уравнение прямой.
В декартовых координатах каждая прямая определяется уравнением первой степени и, обратно, всякое уравнение первой степени с двумя переменными х и у определяют относительно этой системы прямую линию.
Уравнение вида
Ах + Ву + С = 0 (14.1)
называется общим уравнением прямой, здесь 
какие угодно постояные, причем из постоянных и 
хотя бы одна отлична от нуля. Эта прямая ортогональна вектору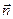 
= 
– нормальному вектору прямой.
В самом деле уравнение (14.1) имеет хотя бы одно решение х0, у0, т. е существует точка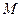 
(х0,у0), координаты которой удовлетворяют уравнению (14.1):
Ах0 + Ву0 +С = 0.
Вычитая это уравнение из (5.1), получим уравнение прямой, проходящей через точку
А(х – х0) + В(у – у0) = 0 (14.2)
Это уравнение определяет прямую, проходящую через точку 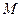(х0,у0) и перпендикулярную вектору =
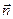Если два общих уравнения 
и 
определяют одну и ту же прямую, то их коэффициенты пропорциональны 
.
Общее уравнение прямой Ах + Ву + С = 0 называется полным, если все коэффициенты ¹ 0. Если хотя бы один из них равен нулю, то уравнение называется неполным.
С = 0: Ах + Ву = 0 – прямая, проходящая через начало координат.
В = 0: Ах + С = 0 – прямая, перпендикулярная оси 
х ( =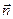 
перпендикулярен оси у).
В = 0; С = 0: Ах = 0– ось у (прямая параллельна у и проходит через начало координат).
Полное уравнение прямой может быть приведено куравнению прямой в отрезках
, (14.3)
где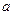 
= - 
; 
= - 
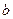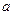.Числа и 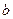равны величинам отрезков, которые отсекает прямая на осях 
и у от начала координат, соответственно. Это уравнение удобно для построения прямой на чертеже.
Пример 14.1. Даны вершины треугольника
Составить уравнение высоты AD.
Решение. Так как высота AD перпендикулярна стороне BC, то вектор 
является вектором нормали для прямой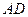 
. Тогда общее уравнение прямой 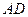имеет вид
или 
