Кривизна поверхности жидкости приводит к появлению сил, действующих на жидкость под этой поверхностью.
Рассмотрим сферическую каплю радиусом 
(рис.7).
При увеличении радиуса сферы растет площадь его поверхности, а вместе с ней и поверхностная энергия. А это может происходить только за счет совершения работы внешними силами. Наоборот, при уменьшении радиуса капли поверхностная энергия уменьшается. Это значит, что работа производится силами, действующими в самой капле. Если на каплю не действуют внешние силы, то они стремятся занять наименьший объем, т.е. объем жидкости под сферической поверхностью всегда несколько сжат. Это приводит к тому, что жидкость в капле испытывает дополнительное давление, направленное радиально перпендикулярно к ее поверхности. Пусть под действием этого давления жидкий шар уменьшит объем на 
. При этом производится работа сжатия жидкости за счет уменьшения поверхностной энергии капли. Работа сжатия 
равна:
, (6.7)
а уменьшение поверхностной энергии 
равна:
, (6.8)
где 
- уменьшение поверхности шара, связанное с уменьшением радиуса капли на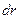 
. Для шара 
и 
. Отсюда следует:
.
Подставляя эти значения для и в (6.7) и (6.8) и принимая во внимание, что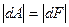 
, получаем:
,
откуда имеем для давления, оказываемого на жидкость ее кривой поверхностью следующее выражение:
. (6.9)
Если поверхность жидкости цилиндрическая, то
,
где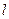 
- длина цилиндра. Соответственно
.
Подставляя эти значения и в формулы (6.7) и (6.8) аналогично получим:
. (6.10)
В общем случае поверхности любой формы давление, обусловленное кривизной поверхности, выражаются уравнением, известным под названием уравнения Лапласа:
, (6.11)
где 
и 
- главные радиусы кривизны для данного элемента поверхности.
В случае сферы = и формула (6.11) переходит в (6.9). В случае цилиндра один из главных радиусов равняется 
, а другой совпадает с радиусом цилиндра. Соответственно, формула (6.11) переходит в (6.10). Дополнительное давление, определяемое формулой (6.11) направлено к центру кривизны поверхности.
Капиллярные явления
В случае, когда жидкость находится в узком сосуде, влияние стенок простирается на всю поверхность жидкости, и она оказывается искривленной на всем своем протяжении.
Если размеры сосуда, в котором находится жидкость, сравнимы с радиусом кривизны поверхности жидкости, то такие сосуды называются капиллярными. Явления, происходящие в таких сосудах, называются капиллярными явлениями.
Рассмотрим некоторые явления, связанные с капиллярностью.
Поскольку в капиллярных сосудах жидкость имеет кривую поверхность, здесь появляется дополнительное давление, вызванное кривизной поверхности. Следствием этого является капиллярный подъем. На рис.8 изображена узкая труба, опущенная в широкий сосуд с жидкостью. Пусть стенки сосуда смачиваются жидкостью. Тогда жидкость, протекающая в трубку, образует вогнутый мениск. Пусть трубка настолько узка, что ее радиус сравним с радиусом 
мениска. Вследствие кривизны мениска появляется дополнительное давление, направленное к центру кривизны мениска, т.е. вверх, равное 
. Под действием этого давления жидкость поднимается по трубке до уровня 
, при котором гидростатическое давление 
столба жидкости высотой , уравновешивают избыточное давление, т.е.
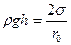, (6.12)
где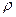 
- плотность жидкости, 
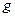- ускорение свободного падения. Из (4.12) следует, что высота подъема жидкости будет равна
. (6.13)
Поскольку радиус кривизны 
трудно определить экспериментально, появляется необходимость выражения через радиус трубки . Для этого воспользуемся рисунком 9.
Центр сферы, частью которой является мениск, находится в точке О. Краевой угол жидкости, соприкасающийся со стенками капилляра, равен 
. Из чертежа видно, что 
. Поэтому формулу (6.13) можно переписать в виде:
. (6.14)
Для жидкости, полностью смачивающей стенки капилляра =0, 
и
. (6.15)
Как следует из (6.15), высота подъема жидкости будет тем больше, чем меньше радиус капилляра и больше коэффициент поверхностного натяжения.
Если жидкость не смачивает капилляр, то картина будет обратной, так как мениск будет выпуклой, а центр кривизны будет находиться внутри жидкости, и давление Лапласа будет направлено вниз. Уровень жидкости в
капилляре будет ниже уровня в сосуде, в который определен капилляр. Разность уровней в этом случае будет также определяться формулой (6.14) или (6.15). Жидкость может подняться вверх и в том случае, когда она находится между пластинами, разделенными узким зазором. Если пластины параллельны друг другу, то мениск имеет цилиндрическую форму, соответственно, дополнительное давление будет равно 
, где 
-радиус мениска. Условие равновесия требует выполнения условия:
, (6.16)
откуда 
. Из рисунка 10 видно, что 
, где 
- расстояние между пластинами. Тогда высоту подъема жидкости можно определить по формуле
. (6.17)
