Если мы возьмем уравнение состояния идеального газа для 1 моля, то
, (5.1)
где под 
подразумевается объем сосуда, в котором заключен газ. Этот объем доступен всем молекулам газа, движущимся в этом сосуде, поскольку молекулы идеального газа не имеют собственного объема и не мешают двигаться друг другу. В действительности же, в газе молекулы не могут занимать весь объем, так как каждая молекула занимает определенную часть сосуда и это часть недоступна для других молекул. Чтобы учесть это, надо из объема сосуда вычесть ту его часть, которая недоступна для движения молекул. Обозначим его через 
. Тогда уравнение (5.1) примет вид:
. (5.2)
Отсюда
. (5.3)
Из этого выражения следует, что при 
, т.е. представляет тот предельный объем, который занял бы газ при бесконечно большом давлении.
Вычислим постоянную . Молекулы не могут сближаться на расстояние, равное нулю даже при бесконечном давлении. Между молекулами существуют силы отталкивания, которые мешают приближаться на расстояние меньше, чем 
. Это минимальное расстояние определяется размерами молекул. Учет размеров молекул означает учет сил отталкивания между частицами.
Предположим, что молекулы представляют твердые шарики. Представим себе сосуд в форме куба, объем которого V (рис.1). Сторона куба равна 
. Пусть диаметр молекулы равен d, а радиус d/2. Допустим, что в нашем кубе содержится одна молекула. Для движения ее центра доступен весь объем сосуда за исключением слоя толщиной r. Это означает, что центр молекулы будет двигаться свободно в объеме 
. Введем еще одну молекулу. Эти молекулы могут приблизиться друг другу не ближе, чем d, т.е. недоступный объем увеличится на 
. Следовательно, для любой из двух молекул оказывается доступным объем, равный
.
Для одного моля, состоящего из 
молекул, каждая из них будет иметь возможность двигаться в объеме
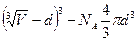. (5.4)
При этом расчете мы не учли то обстоятельство, что в каждом акте сближения участвуют две молекулы. Для каждой из них существенна не вся запретная сфера, окружающая вторую участницу сближения, а только та ее половина (полусфера), которая обращена к ней. Если применять это к любой паре из всех молекул, то в выражении (5.4) вместо необходимо написать 
. Тогда свободным для любой молекулы окажется объем
.
Обычно диаметр молекулы 
, поэтому, пренебрегая 
по сравнению с имеем:
.
Эта и есть та величина 
, которую мы поставили в уравнение состояния (5.2). Следовательно,
.
Таким образом, поправка равна учетверенному объему молекул одного моля газа.
