Прежде отметим достоинство этого уравнения. Уравнение Ван-дер-Ваальса правильно описывает явления, связанные с изменением плотности газов при изменении температуры и давления, взаимные переходы жидкости и газа. Из уравнения Ван-дер-Ваальса вытекает наличие у веществ критической точки. В то же время теория Ван-дер-Ваальса имеет существенные недостатки:
а) Параметры 
и 
, входящие в уравнение Ван-дер-Ваальса не являются постоянными. Они зависят от температуры, хотя по смыслу уравнение Ван-дер-Ваальса и должны быть постоянными, характерными для данного вещества величинами;
б) Другое количественное расхождение между теоретическим уравнением и опытом связано со значениями критических параметров Рк, Vк, Тк. Из системы уравнений (5.8) следует, что между этими величинами должно существовать соотношение:
,
не зависящее от природы вещества. Опыт же показывает, что хотя величина 
постоянна для многих веществ, но равна 3,7. Вместо вытекающего из уравнения Ван-дер-Ваальса соотношения 
, опыт показывает, что значительно лучше выполняется равенство 
. Из приведенных выше параметров следует, что уравнение Ван-дер-Ваальса только качественно правильно описывает явления, происходящие в реальных газах. Для количественных оценок оно является грубым.
В настоящее время принято описывать состояние реального газа более общим уравнением в виде ряда:
Коэффициенты В, С …, которые определяются или из опыта или теоретически, называются вириальными коэффициентами, причем все они зависят от температуры.
Внутренняя энергия газа Ван-дер-Ваальса
Как мы отметили выше, внутренняя энергия неидеальных газов U зависит не только от температуры Т, но и от объема V, т.е.
.
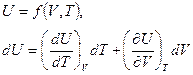Отметим, что 
. Получим выражение для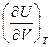 
. С этой целью запишем I закон термодинамики в виде:
.
Тогда
.
Согласно правилам Максвелла, из выражения (1.49), имеем:
.
Таким образом,
. (5.9)
В результате выражение для внутренней энергии газа можно записать в виде:
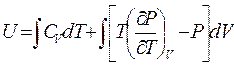. (5.10)
Применим формулу (5.10) для вычисления внутренней энергии газа, описываемого уравнением Ван-дер-Ваальса:
.
В этом случае легко заметить
.
Отсюда
.
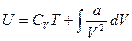Проинтегрировав вторые слагаемые, получим:
,
где В - постоянная интегрирования. Для определения значения В, воспользуемся условием, что при 
, газ становится бесконечно разреженным, т.е. он должен обладать свойствами идеального газа, для которого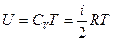 
. Это значит, что 
. Таким образом, внутренняя энергия газа Ван-дер-Ваальса определяется выражением:
. (5.11)
