Аналитический и графоаналитический способы синтеза

 

Программная реализация аналогового РП осуществляется методами, показанными в лабораторной работе № 3 при определении алгоритма работы цифрового ПИД-регулятора скорости, обеспечивающего настройку контура скорости на оптимум по модулю. Отличительной особенностью программной реализации РП является то, что при определении алгоритма его работы необходимо добиться выполнения точностных требований, сформулированных в системе исходных данных, при небольшом перерегулировании и малой колебательности переходных процессов. При решении данной задачи можно выделить два способа ее реализации.

Способ № 1. Аналитический. При определении передаточной функции регулятора положения с помощью программы 1 (см. примеры 4.1, 4.2) можно ограничиться аналитическим решением задачи, которое предполагает использование полной модели РП и позволяет обойтись без построения его ЛАЧХ. Преимущество данного подхода очевидно, так как он не требует графоаналитических построений и расчетов, что в целом упрощает синтез РП. Полученная модель является достаточно точной и при реализации такого регулятора показатели качества процесса управления синтезированной системы совпадают с желаемыми требованиями. Не сложно также произвести дискретную аппроксимацию аналоговой модели РП с применением формулы трапеций. Вместе с тем, несмотря на рациональность и простоту данного способа, он не позволяет адекватно изменить синтезированную модель цифрового РП с целью изменения качества переходного процесса при отработке различных типовых воздействий.

С пособ № 2. Графоаналитический. Применение второго способа, который предполагает графоаналитическое описание при определении структуры и параметров РП (см. лаб. раб. № 4) позволяет, не нарушая требований к заданной точности (ограничение запретной областью), более гибко, настолько, насколько позволяют интуиция и опыт инженера-проектировщика, подойти к вопросу аппроксимации ЛАЧХ РП в области средних частот.

Как известно из теории автоматического управления, высокочастотная область практически не оказывает влияния на качество переходных процессов, поэтому весь упор при подборе параметров РП делается на среднечастотный участок. Так, сдвигая асимптоту, имеющую положительный наклон 20 дБ/дек, влево или вправо, можно уменьшить перерегулирование и колебательность переходных процессов. Кроме того, модель РП, полученная в результате аппроксимации графоаналитическим способом, имеет меньший порядок, чем модель, синтезированная аналитически.

Ниже будут рассмотрены примеры синтеза РП различной конфигурации, а также их программная реализация перечисленными способами.

 

5.2. ПРИМЕР ОПРЕДЕЛЕНИЯ АЛГОРИТМА РАБОТЫЦИФРОВОГО РЕГУЛЯТОРА ПОЛОЖЕНИЯ ДЛЯ ЭЛЕКТРОПРИВОДА
С АСТАТИЗМОМ ВТОРОГО ПОРЯДКА

Пример 5.1. 1. Получить алгоритм работы цифрового регулятора положения для ЭП с астатизмом второго порядка. Числовые значения коэффициентов передаточной функции регулятора принять из примера 4.1 (см. программу 1).

2. Получить алгоритм работы цифрового ПИД-регулятора, передаточная функция которого получена в результате аппроксимации ЛАЧХ (рис. 4.2) в примере 4.1. При решении задачи считать период квантования Т ₀ = 0,001 с.

Решение. 1. Передаточную функцию регулятора положения, полученную с помощью программы 1 (пример 4.1), можно упростить
с применением следующей программы:

>>num=[0.5405 80.31 5964 8679 0];

>>den=[0.07268 42.64 1258 0 0];

>>sys=tf(num, den);

>>minreal(sys)

Transfer function:

7.437 s^3 + 1105 s^2 + 8.206e004 s + 1.194e005

----------------------------------------------

s^3 + 586.7 s^2 + 1.731e004 s

Для определения передаточной функции цифрового регулятора положения W _рп(z) с применением формулы трапеций (bilinear) составим программу в MatLab:

>> num=[7.437 1105 8.206e004 1.194e005];

>> den=[ 1 586.7 1.731e004 0];

>> Fs=1000;

>>[numd, dend]=bilinear(num, den, Fs)

 

numd =

6.1726 -17.6029 16.7515 -5.3210

 

dend =

1.0000 -2.5345 2.0824 -0.5479

В приведенной программе, Fs означает частоту квантования обратно пропорциональную периоду квантования Т ₀. В результате решения получим передаточную функцию цифрового регулятора положения.

Дискретная передаточная функция регулятора положения:

(5.1)

После преобразования будем иметь:

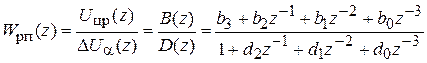. (5.2)

Перепишем (5.2) в виде:

, (5.3)

 

где .

 

. (5.4)

Уравнения (5.3) и (5.4) реализуются в виде структурной схемы непосредственного программирования, которая изображена на рис. 5.1.

 

 

Рис. 5.1. Структурная схема непосредственного программирования цифрового регулятора положения электропривода с астатизмом второго порядка

 

По схеме программирования, представленной на рис. 5.1, находим уравнения состояния и выхода системы.

Уравнения состояния:

 

 

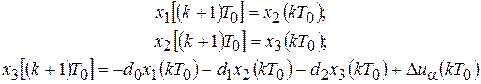
и уравнение выхода:

Векторно-матричная форма уравнений цифрового регулятора положения:

По ним определяем коэффициенты матриц А, B, C и D, соответственно:

(5.5)

2. Передаточная функция ПИД-регулятора положения синтезирована в примере 4.1 и записывается:

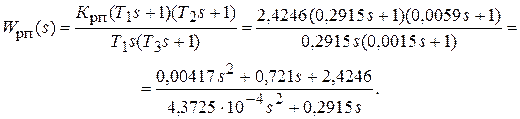
Передаточную функцию цифрового ПИД-регулятора положения определим согласно программе:

>> num=[0.00417 0.721 2.4246];

>> den=[4.3725e-004 0.2915 0];

>> Fs=1000;

>>[numd, dend]=bilinear(num, den, Fs)

 

numd =

7.7720 -14.3031 6.5352

 

dend =

1.0 -1.5000 0.5000

Полученные значения коэффициентов позволяют записать передаточную функцию цифрового ПИД-регулятора:

Для этого выражения удобно использовать метод непосредственного программирования и структурную схему программирования, изображенную на рис. 3.2, которой соответствуют уравнения (3.8) – (3.12).

По уравнениям состояния и выхода системы определяем коэффициенты матриц А, B, C, D:

 

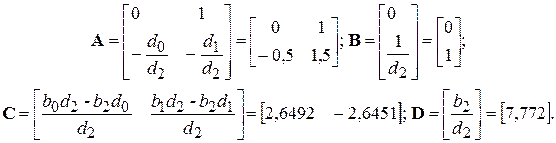(5.6)

 

5.3 ПРИМЕР МОДЕЛИРОВАНИЯ ЭЛЕКТРОПРИВОДА
С АСТАТИЗМОМ ВТОРОГО ПОРЯДКА

Пример 5.2. Составить схему для моделирования электроприводов
с астатизмом второго порядка с цифровыми регуляторами положения, алгоритмы которых рассчитаны в предыдущем примере. Провести моделирование ССДМ с целью сравнения показателей качества переходных процессов. Получить графики системы при отработке задающего и возмущающих воздействий и проанализировать их.

Решение. 1. Составляем схему моделирования электроприводов, изображенную на рис. 5.2. В верхней части рисунка показана ССДМ ЭП
с цифровым регулятором, синтезированным аналитическим способом (Discrete State-Space1).

Рис. 5.2. Схема моделирования электроприводов с астатизмом второго порядка с цифровыми регуляторами поолжения Discrete State-Space1 и Discrete State-Space3

 

 

 

Рис. 5.3. Диалоговое окно блока Discrete State-Space1

 

 

Рис. 5.4. Диалоговое окно блока Discrete State-Space3

На рис. 5.3 показано диалоговое окно блока Discrete State-Space1
с матрицами А, В, С, D и коэффициентами, рассчитанными согласно (5.5).

В нижней части рис. 5.2 показана ССДМ ЭП с цифровым ПИД-регулятором, синтезированным графоаналитическим способом (Discrete State-Space3). Диалоговое окно блока Discrete State-Space3
с коэффициентами матриц А, В, С, D, рассчитанными согласно (5.6), показано на рис. 5.4.

2. Проводим моделирование. Для получения переходных характеристик системы по цепи задающего воздействия в блоках Step и Step1 задаем ступенчатый единичный сигнал. На рис. 5.5 показаны результаты моделирования в виде переходных характеристик системы
по задающему воздействию, которые регистрируются блоком Scope1.

 

a(t), рад

t, c

 

Рис. 5.5. Переходные характеристики системы по задающему воздействию

 

Проведем сравнительный анализ полученных графиков. График 1 является реакцией системы с цифровым регулятором, синтезированным аналитическим способом. График 2 – реакция системы с цифровым ПИД-регулятором. Из анализа графиков видно, что перерегулирование в первом случае составляет не более 23 %; во втором случае перерегулирование не превышает 20 %. При этом быстродействие ЭП с цифровым ПИД-регулятором становится ниже и ПВДУЗ составляет около 0,2 с, тогда как для графика 1 ПВДУЗ практически в два раза меньше и составляет около 0,1 с. В целом, процесс управления с цифровым ПИД-регулятором является более плавным, что благоприятно сказывается на работе ЭП
в режиме слежения.

Для получения графиков ошибок системы на входы ЭП
с различными цифровыми регуляторами необходимо подать квадратично возрастающее задающее воздействие. На схеме (рис. 5.2) данное типовое воздействие сформировано в виде произведения сигналов с выходов блоков Ramp3, Ramp4 и Ramp7, Ramp8. Сигнал с выхода умножителя
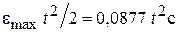= ^-2.

Результаты моделирования регистрируются блоком Scope2 и показаны на рис. 5.6. Из анализа графиков следует, что аналитический способ синтеза цифрового регулятора (график 1) дает более высокую точность и установившаяся ошибка = 0,0033, тогда как цифровой ПИД-регулятор, синтезированный графоаналитическим способом снижает точность примерно в два раза и установившаяся ошибка (см. график 2) = 0,0061. Данное снижение точности может быть вызвано погрешностью графического определения отношения коэффициента передачи ПИД-регулятора к постоянной времени (см. рис. 4.2).

 

t, c

 

Рис. 5.6. Графики ошибок системы
при квадратично возрастающем задающем воздействии

 

На рис. 5.7 показаны графики моментной составляющей ошибки системы при квадратично возрастающем моменте сопротивления, которые регистрируются блоком Scope2. Для получения графиков на схеме (рис. 5.2) данное типовое воздействие сформировано в виде произведения сигналов с выходов блоков Ramp1, Ramp2 и Ramp5, Ramp6. Сигнал
с выхода умножителя .

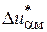
t,c

 

Рис. 5.7. Графики моментной составляющей ошибки системы

при квадратично возрастающем моменте сопротивления

 

Из анализа графиков следует, что моментная составляющая ошибок системы сравнительно невелика и при аналитическом способе синтеза цифрового регулятора (график 1) установившаяся ошибка . Цифровой ПИД-регулятор, синтезированный графоаналитическим способом, снижает точность также примерно в два раза и установившаяся ошибка показана на графике 2.

 

5.4 ПРИМЕР ОПРЕДЕЛЕНИЯ АЛГОРИТМА РАБОТЫ ЦИФРОВОГО РЕГУЛЯТОРА ПОЛОЖЕНИЯ ДЛЯ ЭЛЕКТРОПРИВОДА
С АСТАТИЗМОМ ПЕРВОГО ПОРЯДКА

 

Пример 5.3. Получить алгоритм работы цифрового регулятора положения для ЭП с астатизмом первого порядка. Числовые значения коэффициентов передаточной функции регулятора принять из примера 4.2 (см. программу 1). Получить алгоритм работы цифрового ИД-регулятора, передаточная функция которого получена в результате аппроксимации ЛАЧХ (рис. 4.9) в примере 4.2. При решении задачи считать период квантования Т ₀ = 0,001 с.

Решение. Для упрощения передаточной функции регулятора положения составим программу:

>> num=[4.73 702.7 5.219e004 7.594e004 0];

>> den=[0.1454 85.36 2558 1258 0];

>> sys=tf(num, den);

>> minreal(sys)

Transfer function:

32.53 s^3 + 4833 s^2 + 3.589e005 s + 5.223e005

----------------------------------------------

s^3 + 587.1 s^2 + 1.759e004 s + 8652

Для определения передаточной функции цифрового регулятора положения W _рп(z) с применением формулы трапеций (bilinear) составим программу в MatLab.

>> num=[32.53 4833 3.589e005 5.223e005];

>> den=[ 1 587.1 1.759e004 8652];

>> Fs=1000;

>> [numd, dend]=bilinear(num, den, Fs)

 

numd =

 

26.9936 -76.9804 73.2571 -23.2699

 

 

dend =

 

1.0000 -2.5341 2.0818 -0.5477

Запишем передаточную функцию РП относительно переменной z. Полученная модель по структуре соответствует модели РП из примера 5.1 (см. формулу 5.1). Поэтому, применив схему непосредственного программирования (рис. 5.1), получаем уравнения состояния:

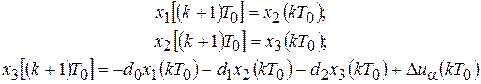
и уравнение выхода:

Векторно-матричная форма уравнений цифрового регулятора положения:

По векторно-матричным уравнениям определяем коэффициенты матриц А, B, C, D, соответственно:

 

; ; .

 

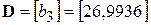Передаточная функция ИД-регулятора положения синтезирована в примере 4.2 и записывается

 

.

 

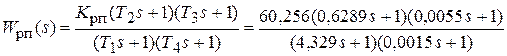Передаточную функцию цифрового ИД-регулятора положения определим согласно программе:

>> num=[0.20842 38.2264 60.256];

>> den=[6.4935e-003 4.3305 1];

>> Fs=1000;

>>[numd, dend]=bilinear(num, den, Fs)

 

numd =

 

26.2788 -48.1360 21.8642

 

dend =

 

1.0000 -1.4998 0.4999

Записываем передаточную функцию цифрового регулятора:

Полученное выражение по своей структуре также совпадает
с передаточной функцией цифрового ПИД-регулятора, рассчитанного
в примере 5.1, поэтому для определения соответствующих матриц воспользуемся аналогичными формулами:

; ; ; .

 

5.5 ПРИМЕР МОДЕЛИРОВАНИЯ ЭЛЕКТРОПРИВОДА
С АСТАТИЗМОМ ПЕРВОГО ПОРЯДКА

 

Пример 5.4. Составить схему для моделирования электроприводов
с астатизмом первого порядка с цифровыми регуляторами положения, алгоритмы которых рассчитаны в примере 5.3. Провести моделирование ССДМ с целью сравнения показателей качества переходных процессов. Получить графики реакции системы при отработке задающего и возмущающих воздействий и проанализировать их.

Рис. 5.8. Схема моделирования электроприводов с астатизмом первого порядка с цифровыми регуляторами положения Discrete State-Space1 и Discrete State-Space3

 

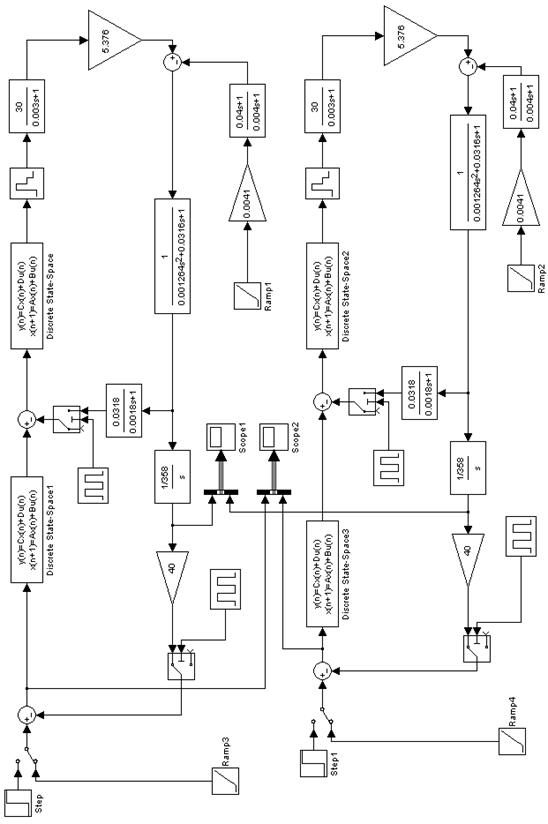
Решение. 1. Составляем схему моделирования электроприводов, изображенную на рис. 5.8. В верхней части рисунка показана ССДМ ЭП
с цифровым регулятором, синтезированным аналитическим способом (Discrete State-Space1). На рис. 5.9 показано диалоговое окно блока Discrete State-Space1 с матрицами А, В, С, D и коэффициентами, рассчитанными согласно (5.4).

 

 

Рис. 5.9. Диалоговое окно блока Discrete State-Space1

 

В нижней части рис. 5.8 показана ССДМ ЭП с цифровым ИД-регулятором, синтезированным графоаналитическим способом (Discrete State-Space3). Диалоговое окно блока Discrete State-Space3
с коэффициентами матриц А, В, С, D, рассчитанными согласно (5.5), показано на рис. 5.10.

2. Проводим моделирование. Для получения переходных характеристик системы по цепи управления в блоках Step и Step1 задаем ступенчатый единичный сигнал. На рис. 5.11 показаны результаты моделирования в виде переходных характеристик системы по задающему воздействию, которые регистрируются блоком Scope1.

 

 

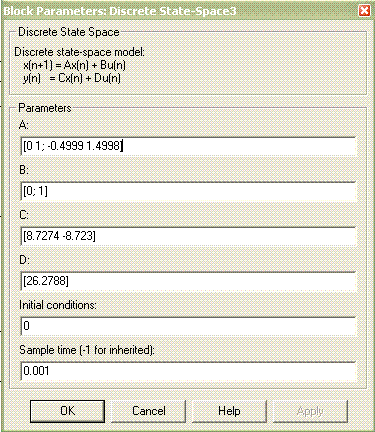
Рис. 5.10. Диалоговое окно блока Discrete State-Space3

 

a(t), рад

t, c

 

Рис. 5.11. Переходные характеристики системы по задающему воздействию

 

Проведем сравнительный анализ полученных графиков. График 1 является реакцией системы с цифровым регулятором, синтезированным аналитическим способом. График 2 – реакция системы с цифровым ИД-регулятором. Из анализа графиков видно, что перерегулирование в первом случае не превышает 36 %; во втором случае перерегулирование составляет 3,7 %. При этом быстродействие ЭП с цифровым ИД-регулятором становится ниже и ПВДУЗ равно 0,088 с, тогда как для графика 1 ПВДУЗ более чем в два раза меньше и составляет примерно 0,04 с. В целом процесс управления цифровым ИД-регулятором является более плавным, что обеспечивает благоприятный процесс слежения в ЭП.

Для получения графиков ошибок системы на входы ЭП
с различными цифровыми регуляторами необходимо подать линейно возрастающее задающее воздействие. На схеме (рис. 5.8) данное типовое воздействие сформировано в виде сигналов с выходов блоков Ramp3 и Ramp4 = = 0,8772 t с^-1

Результаты моделирования регистрируются блоком Scope2 и показаны на рис. 5.12, 5.13.

t, c

 

Рис. 5.12. График ошибки системы при линейно возрастающем

задающем воздействии

 

Из анализа графиков следует, что аналитический способ синтеза цифрового регулятора (график 1) дает более высокую точность и установившаяся ошибка , тогда как цифровой ИД-регулятор, синтезированный графоаналитическим способом значительно снижает точность и установившаяся ошибка (см. график 2) = 0,0035. Данное снижение точности может быть вызвано погрешностью графического определения коэффициента передачи ИД-регулятора (см. рис. 4.9).

 

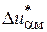
t, c

 

Рис. 5.13. Графики моментной составляющей ошибки системы
при линейно возрастающем моменте сопротивления

 

Из анализа графиков, представленных на рис., 5.13, следует, что моментная составляющая ошибок системы сравнительно невелика и при аналитическом способе синтеза цифрового регулятора (график 1) установившаяся ошибка пренебрежимо мала и составляет . Цифровой ИД-регулятор, синтезированный графоаналитическим способом, снижает точность и установившаяся ошибка, равная 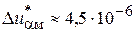, показана на графике 2.

 

Отчетные материалы

1. Структурная схема непосредственного программирования цифровых регуляторов положения.

2. Векторно-матричные разностные уравнения цифровых регуляторов положения.

3. Схемы сравнительного моделирования электроприводов
с астатизмом второго и первого порядка.

4. Графики переходных характеристик и ошибок при отработке управляющих и возмущающих воздействий. Сравнительный анализ графиков.

Контрольные вопросы

1. Пояснить аналитический способ синтеза цифровых регуляторов.

2. Пояснить графоаналитический способ синтеза цифровых регуляторов.

3. Порядок синтеза цифровых регуляторов положения, полученных аналитическим и графоаналитическим способами.

4. Особенности сравнительного моделирования ЦАСУ с астатизмом второго порядка.

5. Особенности сравнительного моделирования ЦАСУ с астатизмом первого порядка.

 

 

 

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

 

1. Башарин А. В., Новиков В. А., Соколовский Г. Г. Управление электроприводами: учеб. пособие для вузов. – Л.: Энергоиздат. Ленингр. отд., 1982.

2. Бесекерский В.А. Цифровые автоматические системы. – М.: «Наука», Главная редакция физико-математической литературы, 1976.

3. Волков Н. И., Миловзоров В. П. Электромашинные устройства автоматики. – М.: Высш. шк., 1986.

4. Динамика систем управления ракет с бортовыми ЦВМ. / Под ред.

М. С. Хитрика, С. М. Федорова. – М.: Машиностроение, 1972.

5. Изерман Р. Цифровые системы управления: Пер. с англ. – М.: Мир, 1984.

6. Куо Б. Теория и проектирование цифровых систем управления. М.: Машиностроение, 1986.

7. Острем К., Виттенмарк Б. Системы управления с ЭВМ: Пер.
с англ. – М.: Мир, 1987.

8. Ротач В. Я. Теория автоматического управления: учеб. для вузов. – 3-е изд., стереот. – М.: Издательство МЭИ, 2005.

9. Системы непрерывного управления электроприводами. /
В. В. Рудаков и др. – Л.: Наука, 1968.

10. Справочник по теории автоматического управления / Под ред.
А. А. Красовского. – М.: Наука. Гл. ред. физ.-мат. лит., 1987.

11. Теория линейных систем автоматического регулирования и управления. / Е. П. Попов. – Гл. ред. физ.-мат. лит. изд-ва «Наука», 1978.

12. Топчеев Ю. Атлас для проектирования систем автоматического регулирования. – М.: Машиностроение, 1989.

13. Ту Ю. Современная теория управления. Пер. с англ. – М.: Машиностроение, 1971.

 

ОГЛАВЛЕНИЕ

 

Введение.............................................
1. Лабораторная работа № 1. Выбор и расчет элементов непрерывной части цифро-аналоговой системы управления
1.1. Анализ структурной схемы цифро-аналоговой системы управления.................................................
1.2. Динамические свойства двигателя постоянного тока с якорным управлением.......................................
1.3. Выбор и расчет двигателя............................
1.4. Пример выбора и расчета двигателя...................
2. Лабораторная работа № 2. Оптимизация контура скорости
2.1 Стандартные настройки и их применение...............
2.1.1. Настройка на оптимум по модулю................
2.1.2. Настройка на симметричный оптимум.............
2.2. Синтез регулятора скорости для настройки контура скорости на оптимум по модулю..............................
2.2.1. Преобразование структурной схемы динамической модели двигателя...........................................
2.2.2. Расчет параметров регулятора скорости и построение структурной схемы динамической модели контура скорости.......
2.3. Пример синтеза регулятора скорости
3. Лабораторная работа № 3. Программная реализация цифрового регулятора скорости и моделирование контура скорости
3.1. Уравнения состояния линейных непрерывных стационарных систем........................................
3.2. Структурные схемы моделирования цифровых систем...
3.3. u-преобразование...................................
3.4. Примеры программной реализации регулятора скорости и моделирования контура скорости..............................
4. Лабораторная работа № 4. Синтез регулятора положения
4.1. Основные этапы синтеза регулятора положения.........
4.2. Пример синтеза регулятора положения в системе с астатизмом второго порядка..................................
4.3. Пример синтеза регулятора положения в системе с астатизмом первого порядка..................................
5. Лабораторная работа № 5. Программная реализация регулятора положения
5.1. Аналитический и графоаналитический способы синтеза..
5.2. Пример определения алгоритма работы цифрового регулятора положения для электропривода с астатизмом второго порядка....................................................
5.3. Пример моделирования электропривода с астатизмом второго порядка............................................
5.4. Пример определения алгоритма работы цифрового регулятора положения для электропривода с астатизмом первого порядка....................................................
5.5. Пример моделирования электропривода с астатизмом первого порядка............................................
Приложение. Система исходных данных...................
Библиографический список..............................

 

 

 

Учебное издание