Т-ма Ролля:
Якщо ф-я f(x) є С  неперервна на відрізку
неперервна на відрізку  диференційована в інтервалі
диференційована в інтервалі  і на кінцях відрізка приймає рівні значення, тоді
і на кінцях відрізка приймає рівні значення, тоді  принаймні одна точка С така, що
принаймні одна точка С така, що 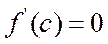 (пох. в ній дор. 0).
(пох. в ній дор. 0).
1) 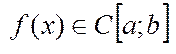
2) 

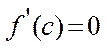
3) 
Доведення: За ІІ теоремою Вейєрштраса всяка неперервна ф-я приймає своє наближене значення.
І) m=M,  , f(x)=C=const, f′(x)=0
, f(x)=C=const, f′(x)=0
II) m<M, f(a)=f(b)
Найб. і найм. знач. не можуть досягти у внутрішній точці С  , тоді за Т. Ролля
, тоді за Т. Ролля  .
.

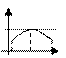
Серед усіх дотичних до кривої у=f(x)  принаймні одна паралельна до Ох.
принаймні одна паралельна до Ох.
Т-ма Лагранжа: Якщоф-я f(x) неперервна на відрізку  , диференційована в інтервалі (a,b), і тоді т. С таке, що має рівність
, диференційована в інтервалі (a,b), і тоді т. С таке, що має рівність  .
.
1) f(x), х 

2) 
Звідси випливає, що  .
.


 .
.
Ця ф-я задов. всім вимогам умови Ролля:
1) 
2о) 
3о)  , тоді за Т. Ролля
, тоді за Т. Ролля 
 ,
,  ,
,


Якщо дотична паралельна до січної, що сполучає точку А і В.
Ф-ла Лагранжа застос. до будь-якого відрізка  або для будь-якого
або для будь-якого
 .
. 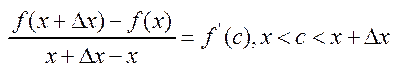 ,
, 
 ,
,  ,
,
 .(с-проміжна точка,
.(с-проміжна точка,
 ).
).
Теорема Коші. Якщо ф-я f(x) і φ(х) неперервні на відрізку  , диференційовані в інтервалі (а,b) при чому φ´(x)≠0, тоді існує принаймні одна т.C, така, що має місце рівність:
, диференційовані в інтервалі (а,b) при чому φ´(x)≠0, тоді існує принаймні одна т.C, така, що має місце рівність:  .
.
1о 
2о  . Звідси випливає
. Звідси випливає  . Якщо покласти φ(x)=x, то
. Якщо покласти φ(x)=x, то 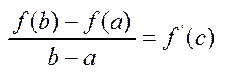 .
.
Доведення: Введемо допоміжну ф-ю  . Ця ф-я задовольняє всім вимогам теореми Ролля. Тоді за Т.Ролля
. Ця ф-я задовольняє всім вимогам теореми Ролля. Тоді за Т.Ролля  ,
,  ,
,
 .
.
Екстремуми ф-ції. Опуклість і точки перегину. Асимптоти.
Необх. умова існув. екстремуму: Якщо  є т. максимуму або мінімуму і в цій т. існує похідна, то ця пох.=0. Для дослідж. ф-ії на екстр. необх. знайти нулі 1-ї похідної і т. в яких вона не існує, дослід. зміну знака 1-ї пох. при переході через крит.точки.
є т. максимуму або мінімуму і в цій т. існує похідна, то ця пох.=0. Для дослідж. ф-ії на екстр. необх. знайти нулі 1-ї похідної і т. в яких вона не існує, дослід. зміну знака 1-ї пох. при переході через крит.точки.
Опуклість.
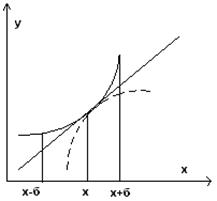
Крива задана р-м y=f(x) назив. вгнутою (опуклою) в т.  , якщо існує такий
, якщо існує такий  окіл цієї точки, що для всіх х з цього околу відповідні точки кривої лежать під (над) дотичною, проведеної до кривої в т.
окіл цієї точки, що для всіх х з цього околу відповідні точки кривої лежать під (над) дотичною, проведеної до кривої в т.  .
.
т.  назив. точкою перегину графіка ф-ії, якщо існують такий
назив. точкою перегину графіка ф-ії, якщо існують такий  окіл цієї точки, що для всіх
окіл цієї точки, що для всіх  всі точки кривої лежать під (над) дотичною, а для всіх правих
всі точки кривої лежать під (над) дотичною, а для всіх правих 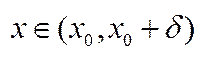 - над (під) дотичною.
- над (під) дотичною.
Теорема. Нехай крива у=f(x) та існує такий  -окіл т.
-окіл т.  , що фун-ія f(x) в околі цієї точки має похідні до другого порядку включно, при чому друга похідна в т. х є неперервна, тоді якщо f ”(x0)>0 – вгнута, f ”(x0)<0 – опукла.
, що фун-ія f(x) в околі цієї точки має похідні до другого порядку включно, при чому друга похідна в т. х є неперервна, тоді якщо f ”(x0)>0 – вгнута, f ”(x0)<0 – опукла.
Доведення: (розглянемо випадок)
Позначимо через у і х відповідно, У= f(x0)- f ‘(x)(х-х0);
у-У= f(x)- f(x0)- f ‘(x)(х-х0);
Запишемо формулу Тейлора для функції:  -
-
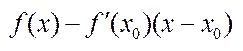 ,
,  ,
, 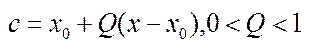 . Якщо друга похідна додатна:
. Якщо друга похідна додатна:
у-Y>0,у>Y, то крива вгнута. Якщо друга пох.<0,то крива опукла.
Асимптоти. Нехай задано y=f(x), f(x) -неперервна. Крива l назив. асимптотою графіка ф-ії y=f(x), якщо відстань від т.М кривої l до даної прямої прямує до нуля, коли т.М рухається в нескінченність, тобто  . Асимптоти бувають: вертикальні(
. Асимптоти бувають: вертикальні( ), горизонтальні(
), горизонтальні( ) і похилі(
) і похилі( ).
). 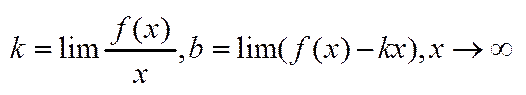 . Якщо хоч одне b або k не існує, то крива не має асимптот.
. Якщо хоч одне b або k не існує, то крива не має асимптот.






