Нехай задана функція 
, 
, 
Визначення 1:
Функція 
назив. неперервною в точці 
, якщо границя функції в цій точці = значенню функції в цій точці.
Визначення 2:
Функція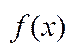 
назив. непер. в точці 
, якщо для будь-якого 
Визначення 3:
Фу-я f(x) назив.непер. в т. 
, якщо якусь послідовність значень 
Властивості фу-й непер. на відрізку:
Теорема Больцано – Коші: Якщо фу-я f(x) неперервна на відрізку 
і на кінцях його має значення, протилежні за знаком, то f(x) обертається в нуль принаймі в одній точці інтервалу (а,в)
Геометрично результат теореми очевидний. Якщо 
, то точки 
лежать у різних напівплощинах. На які вісь 
ділить площину 
. Графік неперервної функції 
, який з’єднує ці точки, обов’язково перетне вісь 
принаймні в одній точці.
Вимога неперервності функції 
на відрізку 
є необхідною: функція, що має розрив хоча б в одній точці, може перейти від від’ємного значення до додатного, не обертаючись у нуль.
Теорема Больцано – Коші (про проміжні значення неперервної функції): Нехай фу-я 
непер. на відр. 
, причому 
. Тоді, яким би не було число С, що стоїть між числами А і В, на відрізку 
знайдеться принаймі одна точка С, така, що 
.
Ці теореми встановлюють, що переходячи від одного свого значення до іншого, функція хоча б один раз набуває кожного свого проміжного значення між її значеннями на кінцях відрізків.
Теорема Веєрштрасса (про обмеженість неперервної на відр. фу-ї): Якщо фу-я непер. на відрізку 
, то вона обмежена на ньому зверху й знизу, тобто існують такі числа m і M, що для всіх х є 
справедлива нерівність 
Поняття рівномірної неперервності: фу-я 
назив. непер. в точці 
де 
на мові екстремум 
якщо для будь-якого 
існує таке 
, що 
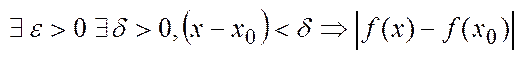
. Фу-я 
, 
назив рівномірно неперервною на проміжку Х, якщо для будь-якого 
, що з нерівності 
слідує нерівність 
, де б ми не взяли 
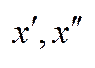з проміжку . Має місце наступна теорема - теорема Кантора: Якщо фу-я 
неперервна на відр. 
, то вона ріваномірно неперервна на ньому.
Доведення: (методом від супротивного) Нехай для даного 
не існує такого 
про яке мова йде в теоремі. Нехай існує таке 
, 
з нерівності 
. Розглянемо послідовність 
- додатніх чисел, таких, що 
, тоді для кожного 
знайдуться на відрізку 
значення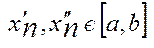 
, такі, що з нерівності 
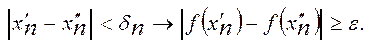Згідно леми Б-В з обмеженої послідовності 
можна завжди виділити збіжну підпослідовність. 
. Тоді в силу неперервності фу-ї в точці 
випливає, що з нерівності 
повинно випливати 
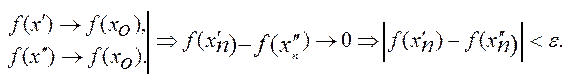Модуль різниці стає як завгодно малий. А це суперечить умові.
Нехай для довільного 
визначені фу-ї 
, розглянемо фу-ю 
(1). Ця фу-я є комплексно значною від дійсної змінної. 
Фу-я 
буде неперервною в т. 
, якщо в цій точці будуть неперервними фу-ї 
і 
. Мають місце всі відомі властивості неперервних фу-й дійсної змінної. Фу-я 
назив. диференційованою в точці 
, якщо в цій точці диференційованими є фу-ї 
і 
і похідна 
Функція комплексної змінної: нехай кожному елементу z з деякої множини Е за певним законом поставимо у однозначну відповідність компл. число із множн. 
, тоді на мн. 
комплексно значна фу-я комплексної змінної. Їх називають комплексними фу-и змінної. 
, 
Фу-я 
наз. неперервною в т. 
якщо вона в цій точці визначена і 
. Фу-я буде неперервною в т. 
якщо неперервними будуть фу-ї 
та 
. Мають місце вл. неперервних фу-й дійсної змінної, а саме:
Якщо 
неперервна в точці , то неперервними в цій точці будуть фу-ї: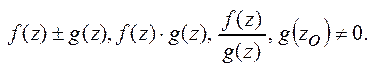 
Неперервною також суперпозиція двох неперервних фу-й.
