Ф-ія, обернена до показникової  (
( ), наз. логарифмічною. Записується:
), наз. логарифмічною. Записується:  , де
, де  - основа, причому
- основа, причому 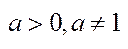 ,
,  - аргумент.
- аргумент.
Властивості: 1)  ; 2)
; 2) 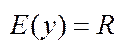 ; 3) Ф-ія ні парна, ні непарна; 4)
; 3) Ф-ія ні парна, ні непарна; 4)  - нуль ф-ції; 5) Ф-ія монотонна: при
- нуль ф-ції; 5) Ф-ія монотонна: при  спадає, а при
спадає, а при  - зростає; 6) При
- зростає; 6) При  :
:  , якщо
, якщо  ;
;  ,якщо
,якщо  . При
. При  :
: 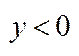 , якщо
, якщо  ;
;  ,якщо
,якщо  .
.
Логарифмічною ф-єю від комплексної змінної  наз ф-ія, обернена до показникової
наз ф-ія, обернена до показникової  (
( ).
).  оскільки ф-ія
оскільки ф-ія  ніколи не приймає значення 0. Позначається
ніколи не приймає значення 0. Позначається  .
.
Знайдемо дійсну і уявну частини ф-ії  .
.
Положим 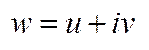 ,
,  , де
, де  ,
,  ,
, 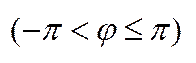 . Тоді маємо
. Тоді маємо  . Прирівнявши модулі і аргументи правих і лівих частин отриманого комплексного рівняння, знаходимо
. Прирівнявши модулі і аргументи правих і лівих частин отриманого комплексного рівняння, знаходимо  ,
,  . Таким чином,
. Таким чином,  ,
, 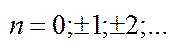 Ввівши позначення, маємо
Ввівши позначення, маємо  . Логарифм (як ф-ія деякої комплексної змінної) нескінченнозначна ф-ія, дійсна частина якої визначається однозначно і дорівнює натуральному логарифму його модуля, а уявна – дорівнює аргументу числа.
. Логарифм (як ф-ія деякої комплексної змінної) нескінченнозначна ф-ія, дійсна частина якої визначається однозначно і дорівнює натуральному логарифму його модуля, а уявна – дорівнює аргументу числа.
Відмітимо особливо важливі часткові випадки.
1.  - додатнє число:
- додатнє число:  . Тоді
. Тоді
 і
і
 …
…
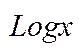 має нескінченну множину значень: …,
має нескінченну множину значень: …,  …, але тільки одне із них (при
…, але тільки одне із них (при  ) дійсне: саме те значення
) дійсне: саме те значення  ,яке відоме із елементарної алгебри.
,яке відоме із елементарної алгебри.
2.  - від’ємне число
- від’ємне число  .Тоді
.Тоді  і для
і для  отримаємо наступні значення:
отримаємо наступні значення:
…,  ….,
….,
( ).
).
Значень 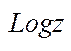 і в цьому випадку буде нескінченна множина, але серед них немає ні одного дійсного. Тому в елементарній алгебрі і стверджують, що не існує логарифма від’ємного числа.
і в цьому випадку буде нескінченна множина, але серед них немає ні одного дійсного. Тому в елементарній алгебрі і стверджують, що не існує логарифма від’ємного числа.
3.Модуль числа  дорівнює одиниці:
дорівнює одиниці: 
 . Тоді
. Тоді  і
і  . Всі значення логарифма числа уявні.
. Всі значення логарифма числа уявні.
Основні властивості логарифмічної ф-ії:
 ,
,  ,
,  .
.
12. Поняття похідної для ф-ій однієї і кількох змінних; геометричний та механічний зміст похідної. Похідні основних елем. ф-ій, правила диференціювання.
Задача про проведення дотичної до кривої.
До даної прямої в даній точці  проведемо дотичну
проведемо дотичну  .
.

Озн. Дотична до кривої, заданої р-ням  наз. граничне положення січної
наз. граничне положення січної  , якщо
, якщо  .
.
 ,
,
 . Звідси
. Звідси

Границя відношення приросту ф-ії до приросту аргументу, якщо  , якщо вона існує, наз. похідною ф-ії
, якщо вона існує, наз. похідною ф-ії  в точці
в точці  .
.
Геометричний зміст. Похідна від ф-ії в даній точці дорівнює кутовому коефіцієнту дотичної до кривої, заданої рівнянням  в точці хо.
в точці хо.
Фізичний зміст. Похідна від шляху по часу = миттєвій шв.або шв. в даний момент часу.
 - р-ня дотичної.
- р-ня дотичної.
 - р-ня нормалі (нормаль – це пряма, перпендикулярна до дотичної).
- р-ня нормалі (нормаль – це пряма, перпендикулярна до дотичної).
Похідні основних елементарних ф-ій.
1.  ;
;
2.  ;
;
3.  ;
;
 ;
;
 ;
;
4.  ;
;
 ;
;
5. 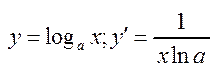 ;
;
 ;
;
6.  ;
;
7.  ;
;
8.  ;
;
9.  ;
;
10.  ;
;
11.  ;
;
12.  ;
;
13. 
 .
.
Операція знаходження похідної даної ф-ії наз.її диференціюванням.
Правила диференціювання.
1) Похідна суми двох диференціальних ф-ій  дорівнює відповідній сумі похідний цих ф-ій.
дорівнює відповідній сумі похідний цих ф-ій.
 .
.
Доведення
Дамо аргументу  приріст
приріст  . Тоді ф-ії
. Тоді ф-ії 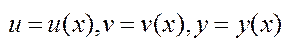 , отримають в свою чергу приріст
, отримають в свою чергу приріст  , оскільки зв’язані рівністю
, оскільки зв’язані рівністю  . Тоді
. Тоді
 .
.
Звідси 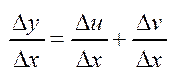 . Знайдемо границю
. Знайдемо границю  , або
, або  , що й треба було доказати.
, що й треба було доказати.
2) Похідна від добутку двох диференціальних функцій  дорівнює сумі добутків першої ф-ії на похідну другої і другої на похідну першої.
дорівнює сумі добутків першої ф-ії на похідну другої і другої на похідну першої. 
3) Сталий множник можна винести за знак похідної. 
4) Похідна від частки двох диференціальних ф-ій  дорівнює дробу, у якого знаменник дорівнює
дорівнює дробу, у якого знаменник дорівнює  , а чисельник дорівнює різниці добутків першої ф-ії на похідну другої і другої на похідну першої.
, а чисельник дорівнює різниці добутків першої ф-ії на похідну другої і другої на похідну першої.
 .
.






